三次贝塞尔(Bezier)曲线

基本定义

三次贝塞尔曲线是由4个控制点定义的参数曲线，是计算机图形学中最常用的贝塞尔曲线形式。

数学公式

给定控制点 ( P_0, P_1, P_2, P_3 )，三次贝塞尔曲线的参数方程为：

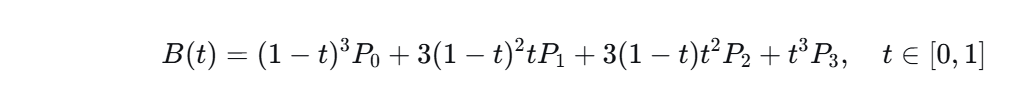
其中：

( t ) 是参数，从0到1变化
各项系数是伯恩斯坦基函数：

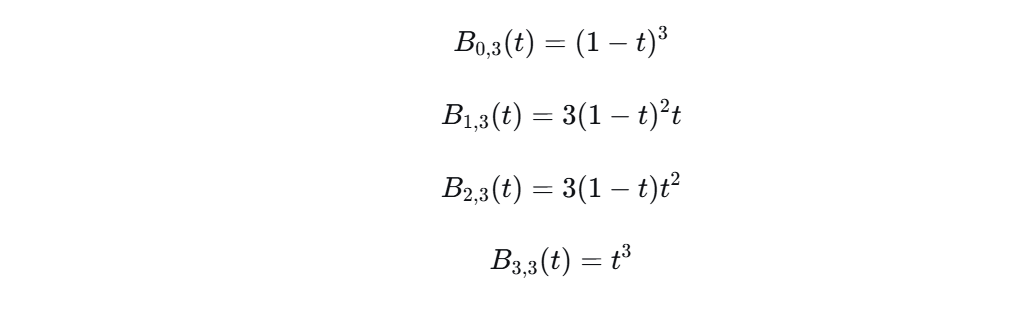
重要特性

端点性质
- ( B(0) = P_0 )，曲线起点在第一个控制点
- ( B(1) = P_3 )，曲线终点在最后一个控制点
端点切线
- 起点切线方向：( P_1 - P_0 )
- 终点切线方向：( P_3 - P_2 )
凸包性：曲线完全位于控制点的凸包内
仿射不变性：对控制点进行仿射变换等价于对曲线进行同样变换

矩阵表示

三次贝塞尔曲线可以用矩阵形式表示：

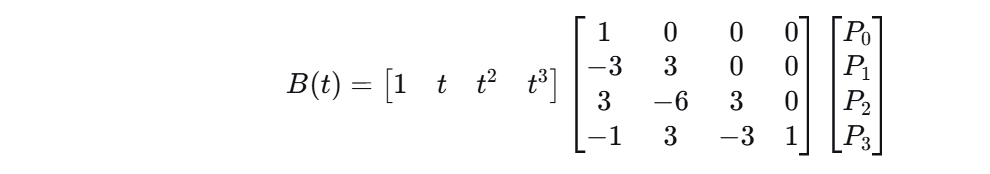
求导公式

一阶导数（切线方向）：

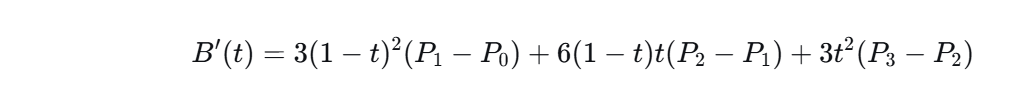
二阶导数：

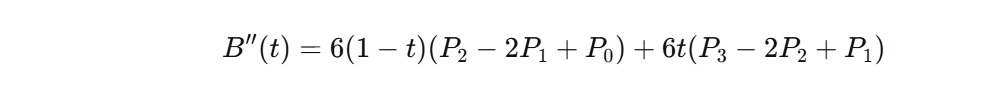
应用示例（代码）

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

def cubic_bezier(t, P0, P1, P2, P3):
    """计算三次贝塞尔曲线上的点"""
    return (1-t)**3 * P0 + 3*(1-t)**2*t * P1 + 3*(1-t)*t**2 * P2 + t**3 * P3

# 控制点
P0 = np.array([0, 0])
P1 = np.array([1, 3])
P2 = np.array([4, 2])
P3 = np.array([5, 0])

# 生成曲线点
t_values = np.linspace(0, 1, 100)
curve_points = np.array([cubic_bezier(t, P0, P1, P2, P3) for t in t_values])

# 绘图
plt.figure(figsize=(8, 6))
plt.plot(curve_points[:, 0], curve_points[:, 1], 'b-', label='贝塞尔曲线')
plt.plot([P0[0], P1[0], P2[0], P3[0]], 
         [P0[1], P1[1], P2[1], P3[1]], 'ro--', label='控制点')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.show()

应用场景

字体设计：TrueType字体使用二次贝塞尔曲线，而PostScript字体使用三次贝塞尔曲线
计算机图形学：路径绘制、动画轨迹
工业设计：汽车、飞机等曲面设计
UI设计：平滑的过渡动画

与二次贝塞尔曲线的比较

特性	二次贝塞尔曲线	三次贝塞尔曲线
控制点数	3个	4个
多项式次数	2次	3次
灵活性	较低，只能形成抛物线	更高，可以形成S形曲线
应用	简单曲线	复杂曲线设计

三次贝塞尔曲线因其灵活性和平滑性，成为矢量图形和曲线设计中最重要的工具之一。