前缀和算法:
一.一维前缀和:
1.构建前缀和数组:
定义一个数组prefix,其中prefix[i]表示数组a的前i项元素和。
初始化prefix[0]=0,然后从1到n依次累加计算前缀和。
数学公式表示为:prefix[i]=prefix[i-1]+a[i]第i项的和表示前i-1项的和加当前项的和。
2.区间和查询
对于任意查询区间([l,r]),其和可以通过以下公式计算:
sum[l,r]=prefix[r]-prefix[l-1];这样我们只需要进行两次数组访问和一次减法操作,时间复杂度为O(1).
举一个基础题例子,解析一下上述算法:
2022年蓝桥杯题目


cs
#include<stdio.h>
typedef long long ll;
#define max_n 200005
int a[max_n];//全局变量,该数组分配在数据段上;栈内存比较小,大数组可能导致栈溢出
ll prefix[max_n];
int main()
{
//函数内部,数组在栈上分配
int n;
scanf("%d",&n);
prefix[0]=0;//定义该数组的初始值为0
int i;
for(i=0;i<n;i++){
scanf("%d",&a[i]);
prefix[i+1]=prefix[i]+a[i]; //前i+1个数的和
}
ll total=prefix[n];//总和
ll ans=0;
for(i=0;i<n;i++){
ll sum_after_i=total-prefix[i+1];//第一次循环算的是减去第一个数其他数的和;
ans+=(ll)a[i]*sum_after_i;//刚好用减去的第一个数用来算乘积
}
printf("%lld\n",ans);
return 0;
}单调队列:
一.单调队列算法整体思路
1.作用:求滑动窗口的最值
求滑动窗口的最大值:
1.整体思路:
单调队列:维护队列里边可能的最大值放在出口。原因就是在某窗口最大值前面的数字肯定是最早被滑出窗口的,那么就不可能是某个窗口的最大值,所以卷走肯定不会受影响。而在某窗口最大值后面的数字更晚滑出窗口,所以后面的数字有可能成为后面窗口的最大值,所以不用管,不能卷走,留到后面看看是否是最大值。这就是要把最大值放在出口的原因。
例如:1 3 -1 -3 5 3 2 1找出其中滑动窗口的最大值。
自定义一个单调栈,有出口和入口。然后将上述8个数字依次拿到栈中,并遵循最大值放在栈出口。首先把1放进来,栈里只有一个数字,1肯定是在出口的最大值。接着把3按原来顺序放在1的后面,3肯定大于1,最大值要放在出口,所以1就要被卷走,之后加-1,-3都不影响,再滑动的时候,之前窗口的最大值就要滑出去了,而是加入5,5比-1,-3都大,所以-1,-3都卷走,要最大值5放在出口。之后依次类推......
因为最大值一直维护在出口处,所以如果弹出的元素和队列出口处的元素相同的话,说明弹出的元素是当前滑动窗口里边的最大值。
二.举洛谷上的例子更好理解:
题目描述
有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如,对于序列 [1,3,−1,−3,5,3,6,7][1,3,−1,−3,5,3,6,7] 以及 k=3,有如下过程:
窗口位置最小值最大值
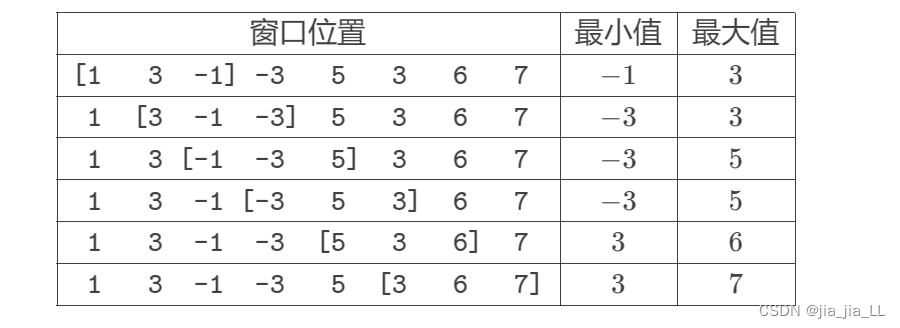
输入格式
输入一共有两行,第一行有两个正整数 n,k。 第二行 n 个整数,表示序列 a
输出格式
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
cs
输入
8 3
1 3 -1 -3 5 3 6 7
输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7
cs
#include <stdio.h>
#include <string.h>
#define MAX_N 1000010
int a[MAX_N]; // 存储输入数组
int op[MAX_N]; // 单调队列,存储下标
int main() {
int n, k;
// 读取输入
scanf("%d %d", &n, &k);
int i;
for (i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
// 第一部分:滑动窗口最小值
int tt = 0, hh = 1; // hh队头,tt队尾
for (i = 1; i <= n; i++) {
// 维护单调递增队列:如果队尾元素大于等于当前元素,则出队
while (hh <= tt && a[op[tt]] >= a[i]) {
tt--;
}
// 将当前元素下标加入队尾
op[++tt] = i;
// 如果队头元素不在当前窗口内,则出队
// 窗口范围:[i-k+1, i]
if (op[hh] < i - k + 1) {
hh++;
}
// 当窗口大小达到k时,输出结果
if (i >= k) {
printf("%d ", a[op[hh]]);
}
}
printf("\n"); // 换行
// 清空队列
memset(op, 0, sizeof(op));//
// 第二部分:滑动窗口最大值
tt = 0, hh = 1; // 重新初始化队列
for (i = 1; i <= n; i++) {
// 维护单调递减队列:如果队尾出口元素小于等于当前元素,则出队
while (hh <= tt && a[op[tt]] <= a[i]) {
tt--;//相当于把出口处的元素给弹出
}
// 将当前元素下标加入队尾
op[++tt] = i;
// 如果队头元素不在当前窗口内,则出队
if (op[hh] < i - k + 1) {
hh++;
}
// 当窗口大小达到k时,输出结果
if (i >= k) {
printf("%d ", a[op[hh]]);
}
}
printf("\n"); // 换行
return 0;
}一.清空队列:void *memset(void *ptr, int value, size_t num);是一个内存操作函数,用于将一段内存区域填充为指定的值。
ptr:指向要填充的内存区域的指针;
value:要设置的值(以int形式传递,但实际按unsigned char处理)
num:要设置的字节数
返回值:返回指向ptr的指针
memset(op, 0, sizeof(op));将op数组的所有字节都设置为0,即将单调队列的字节都设置为0
上述代码保证队列的完全清空。但是在本题中,可以不用清空队列,因为之后重新初始化hh和tt,再进行一次重复操作会将之前的值全部覆盖。
int op[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
// 执行前:op = [1,2,3,4,5,6,7,8,9,10]
memset(op, 0, sizeof(op));
// 执行后:op = [0,0,0,0,0,0,0,0,0,0]
二.解析上述代码求最值过程:
详细执行示例:假设数组a=[5,3,7,1,2],窗口大小为k=3。
1.if (op[hh] < i - k + 1) {
hh++;
}
i-k+1即为窗口的左边界,i为窗口的右边界。当对头下标op[hh]<窗口的左边界,说明对头已经不在窗口内,用这个代码来判断队头元素是否在当前窗口里边。
当i=3时,i-k+1=1,说明下标1还在当前窗口里边op[hh]=op[1]=1;1<1不成立,所以不将下标为1的元素删除;当i=4时,i-k+1=2,说明下标1表示的元素已经不在当前窗口里边了,这时hh++,op[1]=1<2;成立,hh++;删除队头元素;依次类推......i不断累加,hh不断累加,窗口在不断向右移动,左边界元素不断从窗口删除。
2.if (i >= k) {
printf("%d ", a[op[hh]]);
}
上述代码是滑动窗口的结果输出部分;当窗口大小达到k时,输出当前窗口的最值,输出的是队头元素对应的值(因为最值总是被放在出口处,即对头的位置)
i>=k;表示已经有k个连续的元素形成了完整的窗口,输出的a[op[hh]]即为队列队头对应的值,就是当前窗口的最值。当i=3及以后,就可以输出最值了。
3.完整算法流程图:
开始
↓
读取n, k, 数组a
↓
初始化队列:hh=1, tt=0
↓
for i从1到n:
│
├─▶ 维护单调性:移除队尾≥a[i]的元素(最小值队列)
│
├─▶ 插入新元素:op[++tt] = i
│
├─▶ 维护窗口范围:if(op[hh] < i-k+1) hh++
│
└─▶ 输出结果:if(i≥k) 输出a[op[hh]]
↓
结束
4.以数组a=[5,3,7,2,1]求最小值为例:解析上述代码
初始状态:
数组:索引 1 2 3 4 5
值 5 3 7 2 1
队列:hh=1, tt=0(空)
步骤1:i=1 (a[1]=5)
队列操作:
while循环:跳过(队列空)
插入:op[++tt]=1 -> op[1]=1, tt=1
窗口检查:op[1]=1 < 1-3+1=-1? 否
输出检查:i=1 >= 3? 否 -> 不输出
当前队列:op[1]=1(值5)
窗口大小:1(不完整)(当i=1时,还没有形成完整窗口)
步骤2:i=2 (a[2]=3)
队列操作:
while循环:a[op[1]]=5 >= 3? 是 -> tt-- -> tt=0
插入:op[++tt]=2 -> op[1]=2, tt=1
窗口检查:op[1]=2 < 2-3+1=0? 否
输出检查:i=2 >= 3? 否 -> 不输出
当前队列:op[1]=2(值3)
窗口大小:2(不完整)
步骤3:i=3 (a[3]=7)
队列操作:
while循环:a[op[1]]=3 >= 7? 否 -> 跳过
插入:op[++tt]=3 -> op[2]=3, tt=2
窗口检查:op[2]=3 < 3-3+1=1? 否
输出检查:i=3 >= 3? 是 -> 输出 a[op[1]] = a[2]=3
当前队列:op[1]=2 ,op[2]=3(值7)
窗口大小:3(完整窗口 [1,2,3])
输出:7
步骤4:i=4 (a[4]=2)
队列操作:
while循环:第一次循环:a[op[2]]=7 >= 2? 是 -> tt-- -> tt=1
第二次循环:a[op[1]]=a[2]=3>=2成立,->tt--->tt=0
第三次循环,条件不成立
插入:op[++tt]=4 -> op[1]=4, tt=1
窗口检查:op[1]=4<i-k+1=2,否
输出检查:i=4 >= 3? 是 -> 输出 a[op[1]] = a[4] = 2
当前队列:op[1]=4(值2)
窗口大小:3(完整窗口 [2,3,4])
输出:2
步骤5:i=5 (a[5]=1)
队列操作:
while循环:第一次循环:a[op[1]]=a[4]=2 >= 1? 是 -> tt-- -> tt=0
第二次循环:tt=0条件不成立
插入:op[++tt]=5 -> op[1]=5, tt=1
窗口检查:op[1]=5 < 5-3+1=3? 否
输出检查:i=5 >= 3? 是 -> 输出 a[op[1]] = a[5] = 1
当前队列:op[2]=5(值1)
窗口大小:3(完整窗口 [3,4,5])
输出:1
最终输出序列:7 2 1
三.为什么要利用hh和tt?
hh队头指针,指向当前窗口的第一个元素,tt队尾指针,指向当前窗口的最后一个元素,它们共同维护一个双端队列(deque),用于高效解决滑动窗口最值问题。
需要在两端进行操作:1.队尾操作,插入新元素,删除比当前元素"差"的旧元素。2.队头操作,删除移出窗口的元素。
1.tt的作用
while (hh <= tt && a[op[tt]] >= a[i]) {//删除队尾无用元素,维护单调性
tt--;//从队尾删除
}
op[++tt] = i;//插入新元素,在队尾添加
- 检查队尾元素是否需要删除(根据单调性)
- 将新元素添加到队尾
- 保证队列的单调性
2.hh的作用
if (op[hh] < i - k + 1) {//删除移出窗口的元素
hh++;//从队头删除
}
四.让我们用示例 a = [3, 1, 4, 2, 5], k = 3 来演示:(下面的是理解的关键)
初始状态:
队列:[]
hh=1, tt=0//tt表示的是插入元素后的队列元素的下标,而该队列由op[]数组表示,op[]数组的值,即为a数组的下标。如果要在单调队列中删除元素,只需要将队尾的下标删除即可,(因为在刚插入元素的时候,不符合题意的本身就是队尾的元素,所以可以直接用tt--来删除)。之后会有新的元素代替这个被删除元素的下标,那这个被删除的元素就不存在于队列中,反正最后要以该单调队列为准输出。单调队列,目的是让插入元素后的数组的元素按单调性来排列,而不是数组a。再输出最后结果的时候,hh表示队列左边界的下标,op[hh]对应队列左边界的值,a[op[]]即为数组a的某个元素。
i=1 (a[1]=3):
插入后队列:[1] (值3)//第一个元素直接插入单调队列,tt=1,(该单调队列的下标)同时,在a数组中也是第一个元素,下标为1,所以在队列中的值为1.
op[hh]=op[1]=1,(就是队首的元素的值)不符合if (op[hh] < i - k + 1),所以hh=1不变。
窗口:[1] (不完整)
i=2 (a[2]=1):
操作:删除队尾 3(≥1)//当要插入数组a的第二个元素的时候,一开始的时候还没有将1插入,a[2]=1只是当前要插入的元素,,用当前要插入的元素与已经插入的元素进行比较,发现第一个元素3大于1,不符合单调递减的条件,所以要将3删除,tt--,所以tt变成了0,正好进行下面的操作op[++tt],把刚刚要插入的元素插入到队列中,变成队列中的第一个元素
插入后队列:[2] (值1)//2是a数组的下标,tt=1是该队列的下标
op[hh]=op[1]=2;同样不符合if条件语句,所以hh=1不变。
窗口:[1,2] (不完整)
i=3 (a[3]=4):
操作:1 < 4,不删除//直接插入
插入后队列:[2,3] (值1,4)//3是数组a的下标,3对应的队列下标是2
i-k+1=1<2不符合if条件语句hh=1;
窗口:[1,2,3] (完整)
队头:a[2]=1 (最小值 ✓)
i=4 (a[4]=2)://要开始正式输出了
操作:删除队尾 4(≥2)
插入后队列:[2,4] (值1,2)
i-k+1=2=2;不符合if条件语句;
窗口:[2,3,4] (完整)
队头:a[2]=1 (最小值 ✓)//因为hh不变为1,所以输出的是队首
i=5 (a[5]=5):
操作:2 < 5,不删除
插入后队列:[2,4,5] (值1,2,5)
窗口检查:队头下标2 < 5-3+1=3? 是 → hh++ → hh=2
更新队列:[4,5] (值2,5)
窗口:[3,4,5] (完整)
队头:a[4]=2 (最小值 ✓)