线性是如何准确定义的?
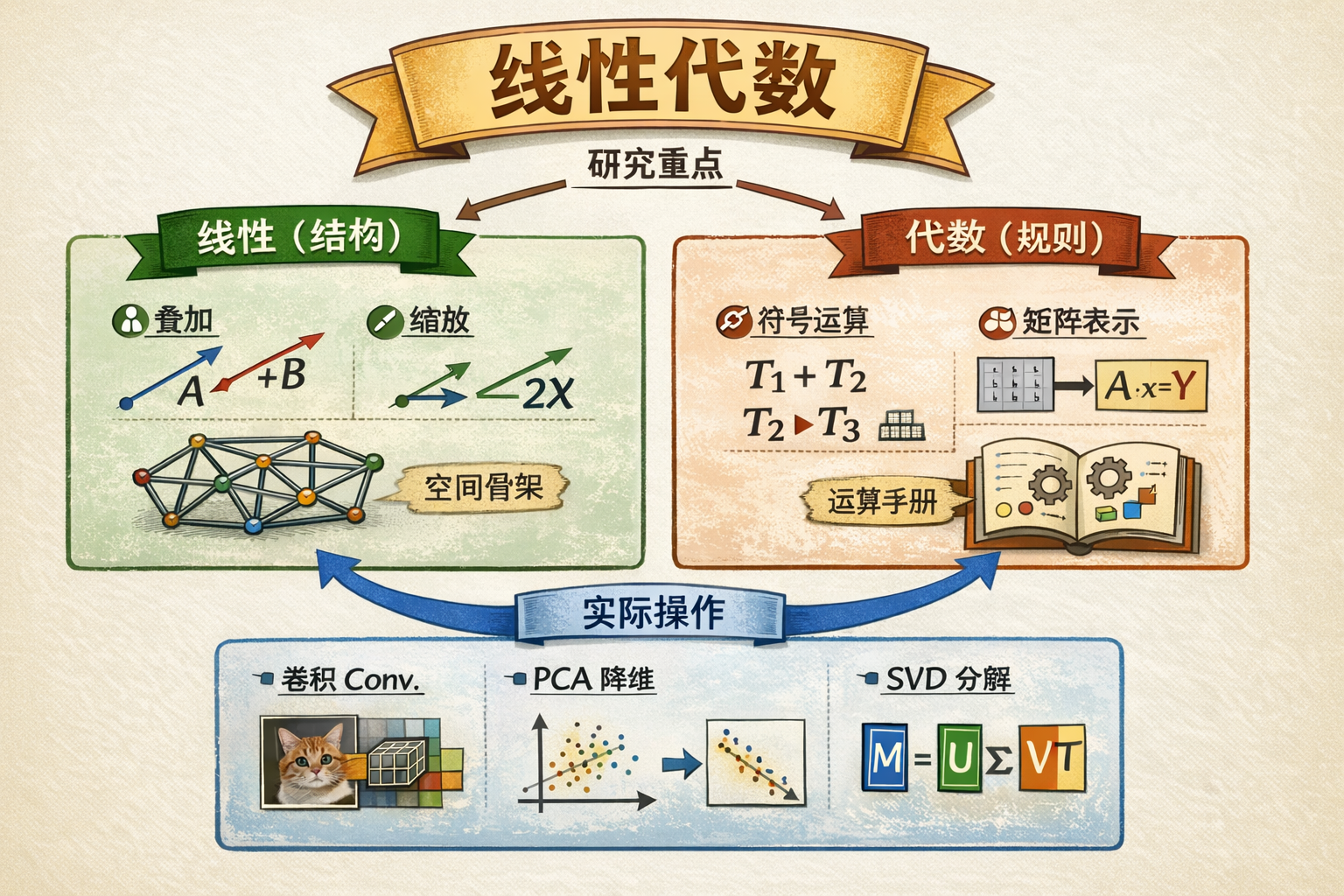
在数学中,线性的定义主要通过两个基本的性质来体现:加法封闭性和数乘封闭性。这两个条件一起确保了操作或关系在执行过程中保持了加法和数乘的结构。
- 加法封闭性
如果一个操作是线性的 ,那么它必须满足加法封闭性,即对于任意两个对象
xxx和yyy进行加法后,再进行变换的结果应该等于先分别对xxx和yyy进行变换,再进行加法。也就是说,变换保持了加法结构。公式化表达为:
T(x+y)=T(x)+T(y) T(x+y)=T(x)+T(y)T(x+y)=T(x)+T(y)
这里 TTT 是一个线性变换操作,表示你对向量xxx和yyy做加法后,再做变换,结果应该与先分别对
xxx 和 yyy 做变换,然后再加起来是一样的。
- 数乘封闭性
线性操作还必须满足数乘封闭性,即对于任意一个标量 ccc 和对象 xxx,我们有:
T(c⋅x)=c⋅T(x)T(c⋅x)=c⋅T(x)T(c⋅x)=c⋅T(x)
也就是说,你可以先对对象进行数乘,再进行变换,或者先进行变换,再进行数乘,结果是一样的。
当一个操作同时满足这两个条件时,我们就称这个操作为线性操作,而这个操作作用的对象(如向量、函数等)也被称为线性的。