文章目录
选数
题目描述
题目解析
本题的搜索思路和上一章介绍的组合型枚举基本相同,无非就是多了一个判断是否是素数,我们采用试除法,将目标数字num分别与2-根号下num相除,如果所有数都除不尽则为素数。
另外因为本题不用输出选择的数,只用判断决策树路径数之和是否为素数,所以本题的全局变量不用拿vector数组存储,用一个整型变量path表示当前路径数之和即可,每一个dfs前后做出选择和恢复现场只用对path做操作。
代码
cpp
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
const int N = 25;
int n, k;
int a[N]; //存储n个整数
int path; //记录路径中的数之和
int ret; //最终结果
bool isprime(int x)
{
//素数从2开始判断,1既不是素数也不是合数
if (x <= 1)
return false;
for (int i = 2; i <= sqrt(x); i++)
{
if (x % i == 0)
{
return false;
}
}
return true;
}
void dfs(int pos, int begin)
{
if (pos > k)
{
if(isprime(path))
ret++;
return;
}
for (int i = begin; i <= n; i++)
{
path += a[i];
dfs(pos + 1, i + 1); //当前填的第i个,从i + 1开始继续往后填
path -= a[i];
}
}
int main()
{
//处理输入
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
dfs(1, 1);
cout << ret << endl;
return 0;
}飞机降落
题目描述
题目解析
本题我们可能会优先想到用贪心的区间问题解法解决,但是因为本题的数据量比较小:N <= 10,所以我们可以考虑枚举所有情况解决,但是因为本题的N不确定,所以我们不能用for循环枚举,因为无法确定枚举层数,所以需要用搜索枚举。
本题的枚举策略是先枚举N个数的全排列,之前我们介绍过。
本题的dfs除了需要传递pos位置,还需要传递上一架飞机的降落结束时间,那么也就是需要算出当前飞机的降落结束时间,飞机的降落结束时间有两种情况,一种是到达机场直接可以降落,降落结束时间为t[i] + l[i],另一种是飞机到来时上架飞机还在占用跑道,需要等待上架飞机降落完毕当前飞机才可以开始降落,降落结束时间为end + l[i],所以本质就是end和t[i]取大再加上l[i]。(补充,计算当前飞机的降落结束时间时不用考虑飞机油量是否足够(是否满足t[i] + d[i] >= end),因为在计算之前若油量不够当前分支已经被剪掉了,如果能走到计算飞机的降落结束时间这里说明油量一定足够)
在枚举过程中需要进行剪枝,本题有三处需要剪枝:1、因为枚举全排列,所以需要一个st数组存储选择过的飞机编号,若选择过则直接continue,递归下一种情况。
2、本题的dfs除了需要传递pos位置,还需要传递上一架飞机的降落结束时间,因为当前飞机需要判断比较飞机最晚起降时间(t[i] + d[i] )和上一架飞机的降落结束时间(end),如果飞机最晚起降时间小于上一架飞机的降落结束,说明当前飞机的油量不足以支撑到上一架飞机的降落结束,需要将该分支剪掉,也就是continue。
3、当枚举过程中dfs已经返回true了,说明已经有情况分支满足条件了,这时不需要继续向后枚举了,直接返回true即可。
注意:1、本题我们要通过dfs判断该组数据是否能完成降落任务,所以需要一个bool类型的返回值。
2、多组测试用例需要重置数据,本题只用重置st数组,因为其他数组读入新数据时老数据会被覆盖掉。
代码
cpp
#include <iostream>
#include <string.h>
using namespace std;
const int N = 1e5 + 10;
const int M = 15;
int T, n;
int t[N], d[N], l[N];
bool st[M]; //标记当前路径哪些飞机选择过
//pos为当前选择第几架飞机, end为上一架飞机的降落结束时间
bool dfs(int pos, int end)
{
if (pos > n)
{
//排列完毕并且合法,返回true
return true;
}
for (int i = 1; i <= n; i++)
{
//剪枝1
if (st[i])
continue;
//剪枝2,若当前飞机最晚起降时间小于上一架飞机的结束时间
// 说明当前飞机无法降落,因为油量无法支持
if (t[i] + d[i] < end)
return false;
st[i] = true;
//最优情况当前飞机从t[i]时刻开始下降,但若上一架飞机
//还在占用跑道需要等待它降落再开始下降,故用max
int newend = max(t[i], end) + l[i];
//剪枝3,假设若1__分枝已经有情况枚举成功,
// 不用再向后枚举了,直接返回true
if(dfs(pos + 1, newend)) return true;
st[i] = false;
}
//走到这里表示for循环枚举的所有情况没有一个符合条件
// (因为符合条件的已经return true了)
return false;
}
int main()
{
cin >> T;
//T组数据
while (T--)
{
//多组测试用例需重置数据
memset(st, 0, sizeof(st));
cin >> n;
for (int i = 1; i <= n; i++)
{
//到达时间,可以盘旋时间,降落花费时间
cin >> t[i] >> d[i] >> l[i];
}
//刚开始结束时间end从0开始
if (dfs(1, 0))
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}八皇后
题目描述

题目解析
八皇后的原题背景是国际象棋,国际象棋中的皇后棋子的行动范围是一行、一列、主对角线和副对角线,如下图所示,本题题意就是在棋盘上摆放皇后旗,让任意两个皇后棋不会互相打起来。
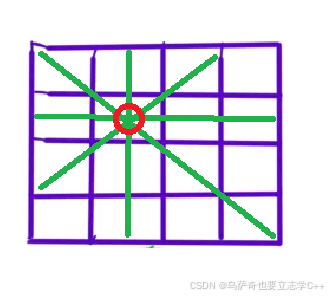
本题利用暴搜解决,思路是每一行放置一个棋子,第一行随机挑选一个位置放置,然后依据第一行棋子的位置,判断第二行棋子可以摆放的位置,本题的难点是剪枝策略,也就是如何判断两颗棋子是否会打起来。
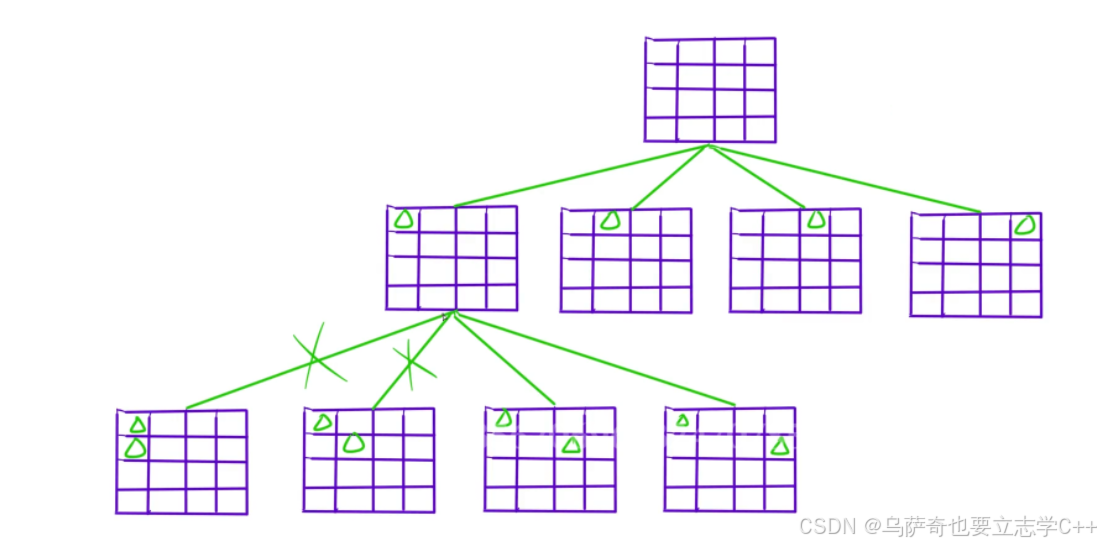
首先行我们不用判断,因为我们就是按行的顺序摆放的。 然后判断列,我们用一个bool数组col标记哪些列摆放过。
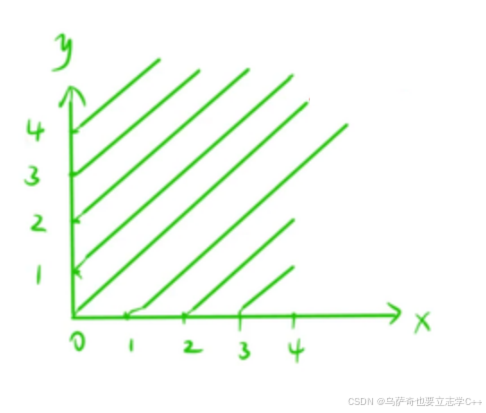
最后是判断主对角线和副对角线,这里我们利用一次函数进行标记,我们知道主对角线的函数为y = x + b, 副对角线函数为y = -x + c,根据一次函数的性质每一个主对角线都有一个唯一的b,每一个副对角线都有一个唯一的c,我们利用两个st数组:st1标记哪些主对角线摆放过和st2标记哪些副对角线摆放过,当填入一个棋子时,我们把棋子的下标(x, y)转化为 y - x,和y + x,将 对应的对应的st数组置为true,但是这里需要注意两个点:
1、y - x是可能出现负值的,因为y - x对应的是数组下标,所以y - x需要加上一个大于等于n的偏移量,将 y - x 的值映射为非负。
2、因为主对角线和副对角线的情况比较多,如下图所示,所以开st1和st2数组空间时需要多开一倍。
代码
cpp
#include <iostream>
#include <vector>
using namespace std;
const int N = 14;
int n;
int ret; //解的总数
vector<int> path; //存储每种解
bool col[N]; //标记哪些列放过
bool st1[2 * N]; //标记主对角线放过
bool st2[2 * N]; //标记哪些副对角线放过
void dfs(int x)
{
if (x > n)
{
ret++;
if (ret <= 3)
{
for (auto& e : path)
{
cout << e << " ";
}
cout << endl;
}
return;
}
for (int y = 1; y <= n; y++)
{
if (col[y] || st1[y - x + n] || st2[y + x])
continue;
col[y] = st1[y - x + n] = st2[y + x] = true;
path.push_back(y);
dfs(x + 1);
col[y] = st1[y - x + n] = st2[y + x] = false;
path.pop_back();
}
}
int main()
{
cin >> n;
dfs(1);
cout << ret << endl;
return 0;
}数独
题目描述

题目解析
本题题意是在一个9 * 9二维数组中,每一行、每一列、每一个紫色方框都只能有1-9这9个数字,不能有重复的数字。
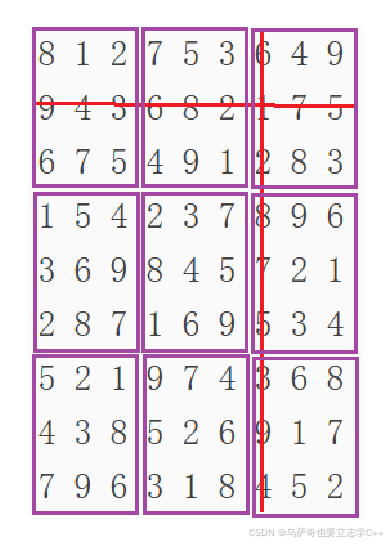
思路依旧用暴搜解决,一个格子一个格子的填数,每个格子从1-9依次尝试,找到一个合法的数填入。
剪枝策略如下:
1、用三个bool类型的数组分别标记某行、某列、某个粗线宫有1-9的哪些数字,如果标记为true,则在dfs枚举1-9数字中直接continue,枚举下一个数字,在处理输入时往格子填数时,若遇到不为0的格子需要将当前格子对应的三个bool类型数组置为true。
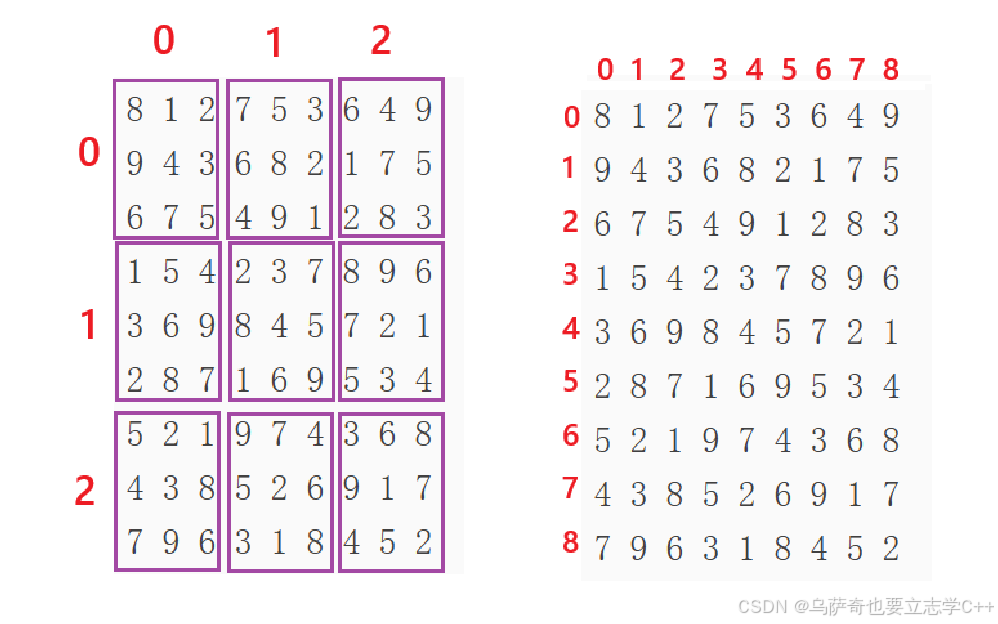
注意:1、本题的粗线宫一共有9个,3 * 3,我们在进行标记时需要找到当前格子对应哪个粗线宫,所以需要将数独棋盘的行、列下标设置为0-8,这样不管是行下标还是列下标,只有除以3就就可以得到粗线宫的下标0-2。
2、本题只要找到一种合法情况就可以递归返回了,所以dfs需要一共bool返回值。
代码
cpp
#include <iostream>
using namespace std;
const int N = 10;
const int M = 3;
int n = 9;
int a[N][N]; //存储原数独
bool row[N][N]; //行 数 标记某行有1-9的哪些数
bool col[N][N]; //列 数 标记某列有1-9的哪些数
bool st[M][M][N]; //3 * 3 * 10 标记某粗线宫有1-9的哪些数
bool dfs(int x, int y)
{
if (y == n)
{
//枚举到了最后一列的下一列,换下一行
x++;
y = 0;
}
if (x == n)
{
//枚举到了最后一行,找到了一种合法情况,停止递归,返回true
return true;
}
if (a[x][y])
{
//当前格(z, y)已经有数了,枚举下一格
return dfs(x, y + 1);
}
for (int i = 1; i <= 9; i++)
{
if (row[x][i] || col[y][i] || st[x / 3][y / 3][i])
continue;
row[x][i] = col[y][i] = st[x / 3][y / 3][i] = true;
a[x][y] = i;
if (dfs(x, y + 1))
return true;
row[x][i] = col[y][i] = st[x / 3][y / 3][i] = false;
a[x][y] = 0;
}
//走到这里说明这个格子填1-9都不合法,说明前面有某一层的格子填的不合法,需要继续枚举
return false;
}
int main()
{
//初始化
int x = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> a[i][j];
x = a[i][j];
if (x)
{
//x不为零
row[i][x] = col[j][x] = st[i / 3][j / 3][x] = true;
}
}
}
dfs(0, 0);
//输出结果
for (int i = 0; i <= 8; i++)
{
for (int j = 0; j <= 8; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
