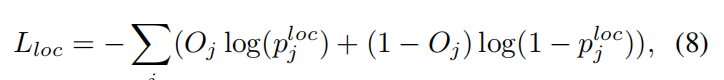一,预测头介绍
论文全称:MTNET: LEARNING MODALITY-AWARE REPRESENTATION WITH TRANSFORMER FOR****RGBT TRACKING

原文相关叙述
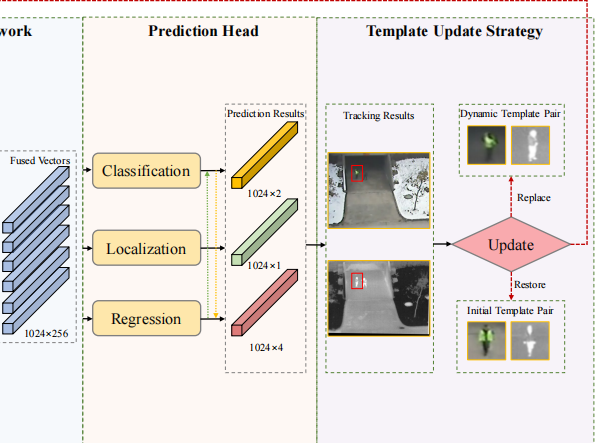
这是原结构图
二,损失函数
1,MTNET总损失函数
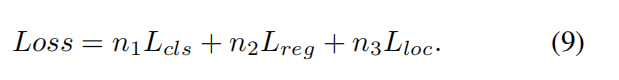
在 MTNet 中,三叉预测头(Trident Prediction Head) 是一种专门设计的多任务学习结构,旨在解决目标跟踪中"分类"与"定位"任务之间的不一致性问题。传统的跟踪器通常只有分类和回归两个分支,但 MTNet 引入了第三个分支,即"定位"分支,从而形成了三路并行的结构。
- 分类分支(Classification):负责判断当前的候选区域(Proposal)究竟是属于目标前景还是背景。它输出一个概率值 p_j,指示该区域包含目标的可能性。
- 回归分支(Regression):负责精细化调整目标的边界框(Bounding Box)。它通过预测坐标偏移量,输出最终的 x, y, w, h,确保框出的目标范围足够准确。
- 定位分支(Localization) :这是 MTNet 的独特之处。它并不是去预测位置,而是去预测该预测框的质量分数,即预测框与真实目标框之间的 IoU 值。这一路分支的作用是为分类结果提供一个"置信度补充"。
这种加权求和的方式使得模型在训练过程中能够同时兼顾三种能力:识标目标、画准边框以及自评质量。通过这三个维度的协同工作,MTNet 能够在复杂背景(如相似物体干扰)中挑选出定位最可靠的结果。
2,损失函数的使用阶段
损失函数(Loss Function)主要存在于训练阶段,而在测试阶段(推理阶段)通常是不计算损失函数的。
- 缺乏标准答案(Ground Truth) :损失函数的核心是计算"预测值"与"真实标签"之间的差距。在真实的测试场景(比如你拿着摄像头实时跟踪一个行人)中,系统并不知道行人的真实精确坐标(也就是没有标签 y_j或
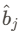 )。既然没有标准答案,也就无法计算出损失值。
)。既然没有标准答案,也就无法计算出损失值。 - 任务性质不同:训练阶段的任务是"学习",目标是最小化损失来更新模型权重;测试阶段的任务是"应用",模型权重已经固定,它的目标是给出最可能的预测结果(比如画出一个框,并给出一个分类得分),而不是为了再次更新自己。
虽然在测试时模型不计算损失函数,但一般会通过评价指标来衡量模型的好坏。这些指标在形式上可能与损失函数有些相似,但用途完全不同:
- 成功率(Success Rate):基于 IoU 阈值判断有多少帧跟踪成功了。
- 精确度(Precision Rate):计算预测中心点与真实中心点之间的距离。 这些指标是给研究人员看的,用来评估模型的整体表现,而不会像损失函数那样反馈给模型去修改参数。
3,损失函数的特殊情况:在线更新(Online Update)
在 MTNet 这种目标跟踪框架中,有一个稍微模糊的区域,即模板更新策略(Template Update Strategy)。
- 在测试过程中,如果目标发生了剧烈的形态变化,模型会根据一些"标准"来决定是否更新跟踪模板。
- 虽然这不叫计算"损失函数"并进行反向传播(那是很耗时的),但它会计算一些置信度分数(类似分类得分 p_j)。如果分数太低,模型可能会判断当前跟踪不可靠,从而触发模板的恢复或替换。
- 例外情况:有一些特殊的算法叫"在线训练跟踪器",它们确实会在测试阶段利用第一帧的标签进行微量、快速的权重更新,这时会用到损失函数。但对于 MTNet 这种基于 Transformer 的主流框架,测试阶段通常是"只看不学"的。
4,损失函数的流向和目的
- 去向 :汇总后的总损失 Loss会被传送到优化器(Optimizer) ,例如 MTNet 中使用的 AdamW。优化器会启动**反向传播(Backpropagation)**算法,沿着梯度的负方向更新网络中成千上万个神经元的权重。这个过程就像在山顶向下走,损失函数提供了斜坡的方向,权重更新则是模型向下迈出的步子,目标是走到损失最小的山谷。
- 正负值 :损失函数通常是正值 (或零)。在数学上,分类公式中虽然出现了 \\log(由于概率在 0 到 1 之间,log 值为负),但公式前面专门加了一个负号(如
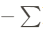 ),就是为了抵消对数带来的负号,从而使总损失变成一个正的"成本"或"代价"。模型的训练目标就是通过不断调整参数,让这个正的代价值无限接近于 0。
),就是为了抵消对数带来的负号,从而使总损失变成一个正的"成本"或"代价"。模型的训练目标就是通过不断调整参数,让这个正的代价值无限接近于 0。
损失函数的设计不仅决定了模型的精度,还决定了训练的难易程度。
三,分类损失
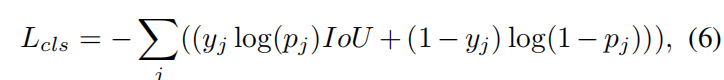
该公式旨在区分目标前景和背景
1,IoU交并比(相关知识)
IoU (Intersection over Union,中文译为交并比)是计算机视觉中衡量两个形状(通常是目标边界框)重叠程度的最常用指标。在目标跟踪和检测任务中,它被用来量化"模型预测的位置"与"真实标注的位置"之间的吻合度。

传统的像素级误差(如L_1损失)有时无法反映真实的重合效果。例如,两个面积很大的框即使中心点离得不远,其重合效果也可能很差;而 IoU 具有尺度无关性,无论目标大小如何,IoU 始终能客观地反映两者的相对重叠质量。在 MTNet 的公式 (6) 和 (8) 中,IoU 就被用作关键的监督信号,指导模型不仅要找对类别,更要画准边框。

2,分类损失函数分析

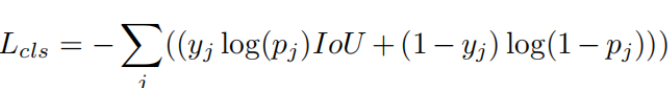

在公式 (6) 和公式 (8) 中使用log运算,其核心逻辑在于将分类问题转化为最大似然估计(Maximum Likelihood Estimation),并在数学上构建一个易于优化的二元交叉熵损失(Binary Cross-Entropy Loss)函数。
从概率论的角度来看,一个预测头输出的p_j代表了该样本属于目标的概率 ,而 (1-p_j) 则代表属于背景的概率 。对于一组独立同分布的样本,我们希望模型输出的概率分布能够最大限度地契合真实的标签。在数学处理上,将多个概率相乘(似然函数)往往会导致数值极小,甚至发生溢出。通过引入对数运算,我们可以将概率的乘法转变为加法,这在计算上更加稳定且高效。
更重要的是对数函数在惩罚错误预测方面的特性。对数函数在接近 0时斜率非常大,这意味着当真实标签为前景(y_j=1)而模型给出的预测概率 p_j 接近 0 时,log(p_j) 会产生一个巨大的负值。通过在公式前面加一个负号,这个巨大的负值就变成了巨大的损失(Penalty)。这种机制强迫模型对那些"错得离谱"的样本产生极大的梯度,从而在反向传播过程中剧烈调整网络权重,使其快速向正确方向收敛。
从信息论的角度理解,这种带有 log 运算的结构实际上是在衡量模型预测的概率分布与真实标签分布之间的"差异"或"惊奇度"。在目标跟踪任务中,由于正负样本(目标和背景)的比例往往极度失衡,这种对错误预测的指数级惩罚能够帮助模型在海量背景干扰中精准锁定目标。在公式 (6) 中,进一步引入 IoU 作为 log(p_j)的系数,实际上是改变了对数函数的斜率,使得那些定位精度越高的样本在产生分类错误时受到的惩罚更重,从而实现了分类得分与定位精度的协同优化。

这样可以:
- 强制关联:它强迫分类分支去学习如何识别那些"高质量"的正样本。只有当一个框既包含目标(语义正确)又紧贴目标(位置准确)时,分类分支才会被要求给出最高分。
- 优化排序:在推理(测试)阶段,我们通常根据分类得分对候选框进行排序。引入 IoU 权重后,最终得分最高的框往往也是定位最准确的框,从而显著提升了跟踪的成功率
四,回归损失

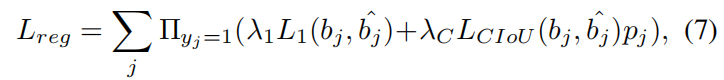

1,L_1损失

2,L_CIoU损失

在 MTNet 中,将 L_1 和 L_{CIoU} 结合在一起是一种"粗调+精调"的策略。L_1 负责让预测框快速飞向目标,而 L_{CIoU} 则通过对距离、形状和重合度的综合建模,确保最终预测的边框不仅位置对,而且长宽比也和目标完全契合
五,定位损失