神经网络的主要特点,就是可以从数据中进行"学习"。这个学习的过程,就是让训练数据自动决定最优的权重参数。
神经网络(深度学习)也是机器学习的一种;跟传统机器学习方法相比,神经网络不需要人工设置 特征量(如 SIFT、HOG等),这样就可以用同样的流程直接处理所有问题了。
1 损失函数
神经网络中,需要以某个指标为线索来寻找最优权重参数;这个指标就是 损失函数(loss function)。
1.1 常见损失函数
(1)均方误差(MSE)
均方误差(Mean Squared Error ,MSE),也称L2 Loss:
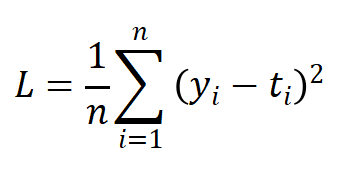
其中,yi表示神经网络的输出,ti表示监督数据的标签(正确的解标签),n则是数据的"维度"。对于固定维度的网络,前面的系数n不重要,因此公式有时也可以写成:
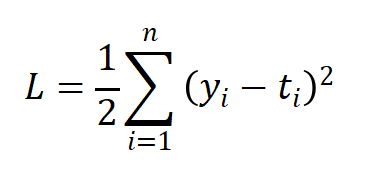
L2 Loss对异常值敏感,遇到异常值时易发生梯度爆炸。
代码实现如下:
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
(2)交叉熵误差
除均方误差之外,交叉熵误差(Cross Entropy Error)也经常被用作损失函数:
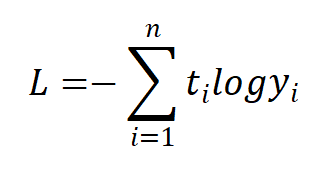
其中,log表示自然对数,yi表示神经网络的输出,ti表示正确解标签;而且,ti中只有正确解标签对应的值为1,其它均为0(one-hot表示)。
代码实现如下:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是 one-hot 向量的情况下,转换为正确解标签的索引
if t.size == y.size:t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
1.2 分类任务损失函数
(1)二分类任务损失函数
二分类任务常用二元交叉熵损失函数(Binary Cross-Entropy Loss)。
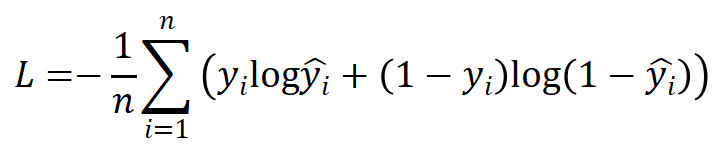
其中:
-
为真实值(通常为0或1)
-
为预测值(表示样本i为1的概率)
(2)多分类任务损失函数
多分类任务常用多类交叉熵损失函数(Categorical Cross-Entropy Loss)。它是对每个类别的预测概率与真实标签之间差异的加权平均。
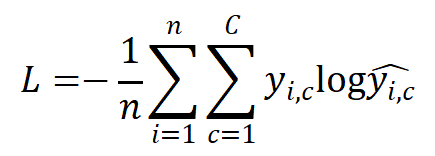
其中:
- C是类别数
为真实值(表示是否为类别c,通常为0或1)
为预测值(表示样本i为类别c的概率)
1.3 回归任务损失函数
(1)MAE
平均绝对误差(Mean Absolute Erro,MAE),也称L1 Loss:
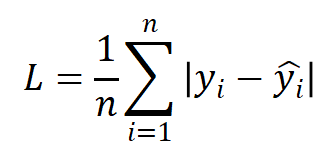
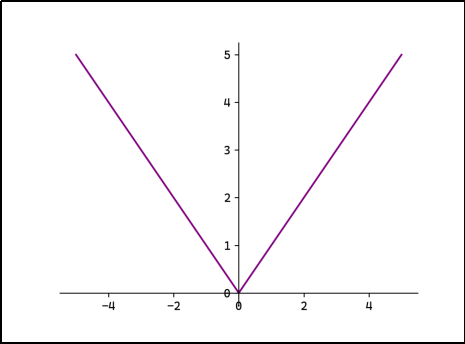
L1 Loss对异常值鲁棒,但在0点处不可导。
(2)MSE
均方误差(Mean Squared Error ,MSE),也称L2 Loss:
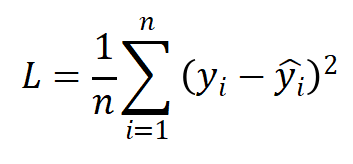
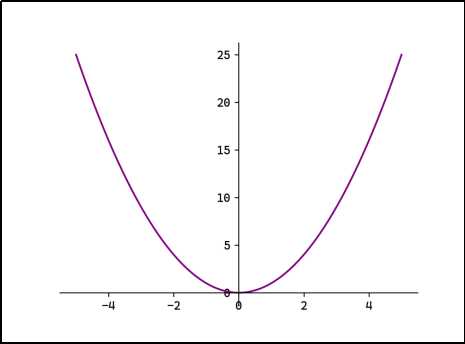
L2 Loss对异常值敏感,遇到异常值时易发生梯度爆炸。
(3)Smooth L1
平滑L1:
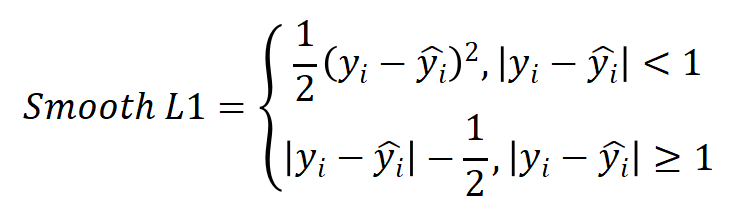
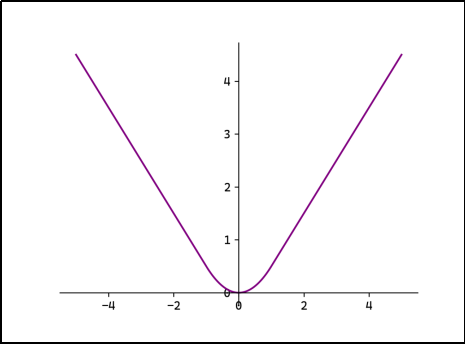
当误差较小时(< 1)使用L2 Loss,使得损失函数平滑可导。当误差较大时(> 1)使用L1 Loss降低异常值的影响。
2 数值微分
损失函数的值越小,代表我们选取的参数越适合;想要求得损失函数的最小值,最基本的想法就是对函数求导,解出导数值为0的点,并判断它是否为极小值/最小值。
然而,实际的函数直接求导,不容易得到解析解。这时可以用数值微分的方式来求某点处的导数,这在工程上应用非常广泛。
2.1 导数与数值微分
在数学上,导数被定义为
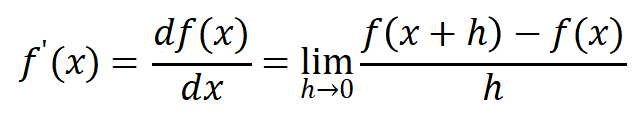
这个定义中表达出了导数的本质。当x 发生一个微小的变化h (或者Δx )时,函数值f(x) 也会发生变化;当h 趋近于0时,此时f(x) 的"变化率"就是x这一点的导数值。
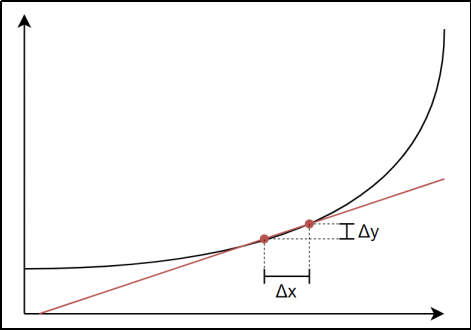
利用这个定义,我们可以直接以数值计算的方式,利用微小的差分来求函数某点处的导数值,这种方法称为 数值微分。
数值微分可以用代码实现非常方便地实现:
def numerial_diff(f, x):
h = 1e-4 # 微小值 0.0001
return (f(x+h) - f(x-h)) / (2 * h)
在这里,我们以x 为中心,计算它两边各发生微小变化后的差分,可以避免只计算单向增大时的误差。这种方法称为 中心差分。
另外,取微小值h时不能太小,这会导致计算机浮点数表示的精度不够,出现舍入误差。
2.2 偏导数
如果函数f的自变量并非单个元素,而是多个元素,例如:
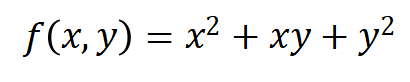
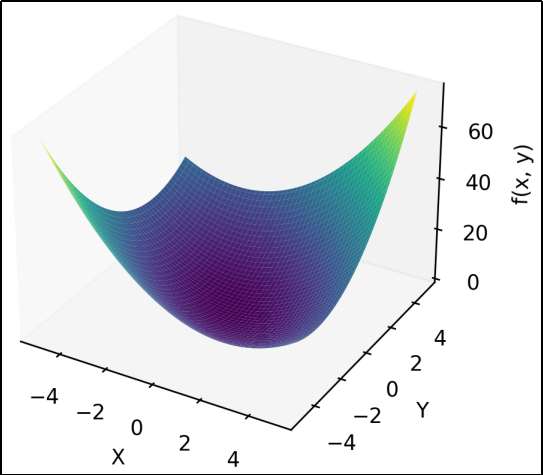

2.3 梯度
多元函数关于每个变量
都有偏导数
,在点
处,这些偏导数定义了一个向量。
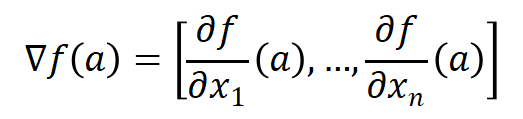
这个向量称为f在点a的梯度。
例如:在(1,1)处的梯度为[3,3]。
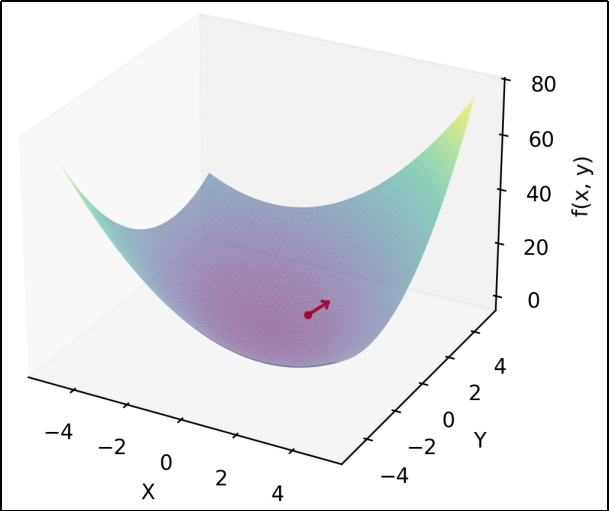
在函数的极小值、极大值和鞍点处,梯度为0。
需要注意的是,梯度代表的其实是函数值增大最快的方向;在实际应用中,我们需要寻找损失函数的最小值,所以一般选择 负梯度 向量。同样地,负梯度代表的是函数值减小最快的方向,并不一定直接指向函数图像的最低点。
利用数值微分,我们可以在代码中实现梯度的计算:
def _numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)x[idx] = tmp_val # 还原值
return grad
3 神经网络的梯度计算
在神经网络的学习中,梯度的计算非常重要。神经网络中的梯度,指的就是损失函数关于权重参数的梯度。
我们以一个单层的简单网络为例,形状为2×3,权重参数为W ,损失函数记为L。那么它的权重参数和梯度为:
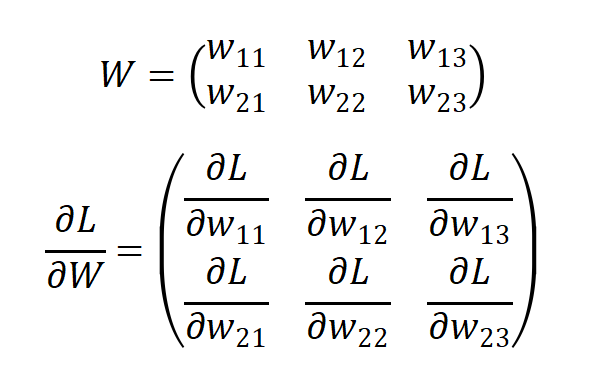
这里,梯度 也是一个2×3的矩阵,其中各个元素由L 关于W中各元素的偏导数构成。
计算这个简单网络的梯度,可以用代码实现如下:
class simpleNet:
def init(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)print(dW)
4 随机梯度下降法
4.1 梯度下降法
****梯度下降法(Gradient Descent)****是一种用于最小化目标函数的迭代优化算法。核心是沿着目标函数(如损失函数)的负梯度方向逐步调整参数,从而逼近函数的最小值。梯度方向指示了函数增长最快的方向,因此负梯度方向是函数下降最快的方向。
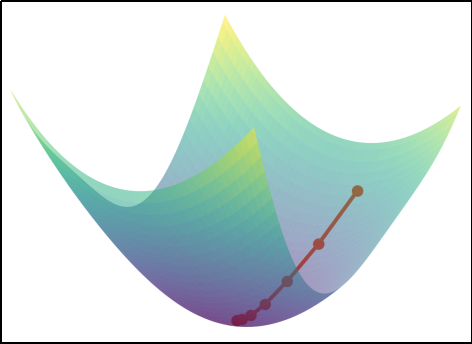
具体来说,我们初始找到函数f (x 1**,x** 2)的一个点(x 1**,x**2),按下式进行更新:
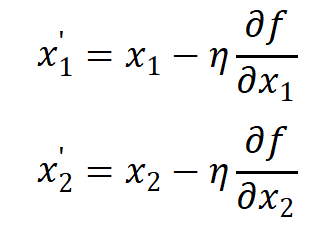
这样就可以沿着负梯度方向,找到一个新的点(x1,x2),让函数值更小。
这里的η表示每次的更新量,在神经网络的学习过程中,就代表了一次学习的步长(一次学习多少、多大程度去更新参数),称为 学习率(learning rate)。学习率需要预先设定好,过大或过小都会导致学习效果不佳。
梯度下降法可以代码实现如下:
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
4.2 模型的训练相关概念
(1)Epoch
1个Epoch表示模型完整遍历一次整个训练数据集的过程。例如,训练10个Epoch表示模型将整个数据集反复学习10次。
模型需要多次遍历数据集(多个Epoch)才能逐步学习数据中的模式,单次遍历数据集(1个Epoch)通常不足以让模型收敛,多次遍历可以逐步优化模型参数。
(2)Batch Size
Batch Size是每次训练时输入的样本数量。例如,Batch Size=32 表示每次用32个样本计算一次梯度并更新模型参数。
小批量数据计算梯度比单样本(Batch Size=1)更稳定,比全批量(Batch Size=全体数据)更高效。并且较小的Batch Size可能带来更多噪声,有助于模型泛化。
(3)Iteration
一次Iteration表示完成一个Batch数据的正向传播(预测)和反向传播(更新参数)的过程。
例如,数据集现有2000个样本,对其训练10个Epoch,选择Batch Size=64:
Batch个数为2000//64+1=31+1=32个(最后一个Batch仅有16个样本)。
每个Epoch中迭代次数Itreation=32次。总迭代次数为10×32=320次。总训练样本数为10×2000=20000。
(4)SGD
在神经网络的学习过程中,可以使用梯度下降法来更新参数,目标就是减小损失函数的值。
实际操作时,一般会从训练数据中随机选择一个小批量数据(mini-batch),然后用梯度下降法迭代多个轮次(iteration);这种"对随机选择的数据进行的梯度下降法",被称作 随机梯度下降法(stochastic gradient descent,SGD)。
具体过程如下:
1)随机选择批数据(mini-batch)
从训练数据中随机选出一部分数据,学习的目标就是要减少这个mini-batch数据的损失函数值。
2)计算梯度
对当前的各权重参数,计算出梯度的值,负梯度就表示了损失函数减小最多的方向。
3)更新参数
按照3.4.1节中梯度下降法的公式,对权重参数沿负梯度方向进行微小更新。
4)重复迭代
重复上面的步骤1)2)3),直到完成预定的总迭代次数。
5 代码实现
使用梯度下降训练的手写数字识别
python
"""
================================================================================
神经网络模型定义文件 - model.py
================================================================================
【文件功能】
这个文件定义了一个三层神经网络模型,用于手写数字识别任务(0-9)
【什么是神经网络?】
神经网络是模仿人脑神经元工作方式的计算模型:
- 人脑有很多神经元,它们通过连接传递信号
- 神经网络也有很多"节点"(神经元),通过"权重"连接
- 信号从输入层进入,经过隐藏层处理,最后从输出层输出结果
【本模型的结构】
输入层(784个神经元) → 隐藏层1(50个神经元) → 隐藏层2(100个神经元) → 输出层(10个神经元)
为什么是784?因为手写数字图片是28x28像素,28×28=784
为什么输出是10?因为数字有0-9共10个类别
【SGD (随机梯度下降) 优化器说明】
SGD是最基础的优化算法:
1. 随机选取一小批数据(batch)
2. 计算这批数据的损失
3. 计算梯度(损失对每个参数的导数)
4. 按照梯度的反方向更新参数
5. 重复以上步骤
公式:新参数 = 旧参数 - 学习率 × 梯度
================================================================================
"""
# ==================== 导入必要的库 ====================
import numpy as np # NumPy是Python的数值计算库,用于矩阵运算
class NeuralNetwork:
"""
三层神经网络模型类
【类的作用】
这个类封装了神经网络的所有功能:
1. 初始化网络参数(权重和偏置)
2. 前向传播(从输入计算输出)
3. 反向传播(计算梯度并更新参数)
4. 预测(给定输入,预测数字类别)
5. 保存/加载模型参数
【网络结构详解】
┌─────────────┐ ┌─────────────┐ ┌─────────────┐ ┌─────────────┐
│ 输入层 │ │ 隐藏层1 │ │ 隐藏层2 │ │ 输出层 │
│ 784个节点 │ ──→ │ 50个节点 │ ──→ │ 100个节点 │ ──→ │ 10个节点 │
│ (28x28像素) │ │ (ReLU激活) │ │ (ReLU激活) │ │(Softmax激活)│
└─────────────┘ └─────────────┘ └─────────────┘ └─────────────┘
↑ ↑ ↑ ↑
W1,b1 W2,b2 W3,b3 概率分布
【参数说明】
- W1: 形状(784, 50) - 输入层到隐藏层1的权重矩阵
- b1: 形状(1, 50) - 隐藏层1的偏置向量
- W2: 形状(50, 100) - 隐藏层1到隐藏层2的权重矩阵
- b2: 形状(1, 100) - 隐藏层2的偏置向量
- W3: 形状(100, 10) - 隐藏层2到输出层的权重矩阵
- b3: 形状(1, 10) - 输出层的偏置向量
"""
def __init__(self, input_size=784, hidden1_size=50, hidden2_size=100, output_size=10):
"""
初始化神经网络
【__init__是什么?】
这是Python类的"构造函数",当你创建这个类的实例时会自动调用
例如:model = NeuralNetwork() 时就会执行这个函数
【参数解释】
- input_size: 输入层的神经元数量,默认784(28×28像素的图片)
- hidden1_size: 第一个隐藏层的神经元数量,默认50
- hidden2_size: 第二个隐藏层的神经元数量,默认100
- output_size: 输出层的神经元数量,默认10(0-9共10个数字)
【为什么要设置这些参数?】
- 输入层大小必须匹配图片像素数
- 隐藏层大小可以调整,影响模型的"学习能力"
- 输出层大小必须匹配类别数量
"""
# -------------------- 保存网络结构参数 --------------------
self.input_size = input_size # 保存输入层大小
self.hidden1_size = hidden1_size # 保存隐藏层1大小
self.hidden2_size = hidden2_size # 保存隐藏层2大小
self.output_size = output_size # 保存输出层大小
# -------------------- 创建参数字典 --------------------
# params字典用于存储所有的权重(W)和偏置(b)
# 权重(W): 连接两层神经元的"强度"
# 偏置(b): 每个神经元的"基础激活值"
self.params = {}
# 调用参数初始化函数
self._initialize_parameters()
def _initialize_parameters(self, initialization='xavier'):
"""
初始化网络参数(权重和偏置)
【为什么需要初始化?】
神经网络开始训练前,需要给权重和偏置一个初始值
如果初始化不好,网络可能:
1. 无法学习(梯度消失)
2. 学习不稳定(梯度爆炸)
【Xavier初始化是什么?】
Xavier初始化是一种聪明的初始化方法:
- 让每层的输出方差保持一致
- 公式:权重 ~ N(0, 1/n),其中n是输入的神经元数量
- 这样可以让信号在网络中平稳传递,避免梯度问题
【参数解释】
- initialization: 初始化方法,'xavier'或'random'
"""
if initialization == 'xavier':
# ==================== Xavier初始化 ====================
# 这种初始化方法考虑了输入的维度,使训练更稳定
# W1: 输入层(784) → 隐藏层1(50)
# 形状: (784, 50),即784行50列的矩阵
# np.random.randn生成标准正态分布的随机数
# 乘以 sqrt(1/输入维度) 来缩放
self.params['W1'] = np.random.randn(self.input_size, self.hidden1_size) * np.sqrt(1. / self.input_size)
# W2: 隐藏层1(50) → 隐藏层2(100)
# 形状: (50, 100)
self.params['W2'] = np.random.randn(self.hidden1_size, self.hidden2_size) * np.sqrt(1. / self.hidden1_size)
# W3: 隐藏层2(100) → 输出层(10)
# 形状: (100, 10)
self.params['W3'] = np.random.randn(self.hidden2_size, self.output_size) * np.sqrt(1. / self.hidden2_size)
else:
# ==================== 简单随机初始化 ====================
# 用很小的随机数初始化(乘以0.01)
self.params['W1'] = np.random.randn(self.input_size, self.hidden1_size) * 0.01
self.params['W2'] = np.random.randn(self.hidden1_size, self.hidden2_size) * 0.01
self.params['W3'] = np.random.randn(self.hidden2_size, self.output_size) * 0.01
# ==================== 偏置初始化为0 ====================
# 偏置通常初始化为0
# 形状都是(1, 该层神经元数量),方便广播运算
self.params['b1'] = np.zeros((1, self.hidden1_size)) # (1, 50)
self.params['b2'] = np.zeros((1, self.hidden2_size)) # (1, 100)
self.params['b3'] = np.zeros((1, self.output_size)) # (1, 10)
def relu(self, x):
"""
ReLU激活函数 (Rectified Linear Unit,修正线性单元)
【什么是激活函数?】
激活函数给神经网络引入"非线性"
没有激活函数,多层神经网络等价于单层(因为线性的组合还是线性)
有了激活函数,网络才能学习复杂的模式
【ReLU函数】
公式:f(x) = max(0, x)
- 如果x > 0,输出x
- 如果x ≤ 0,输出0
图示:
↑ 输出
│ ╱
│ ╱
│ ╱
──────────┼──╱─────→ 输入
│
【为什么用ReLU?】
1. 计算简单快速
2. 减少梯度消失问题(正数区域梯度恒为1)
3. 让神经元输出更稀疏(很多输出为0)
【参数和返回值】
- x: 输入数据(numpy数组)
- 返回: 应用ReLU后的结果
"""
return np.maximum(0, x) # np.maximum逐元素取较大值
def relu_derivative(self, x):
"""
ReLU函数的导数,用于反向传播
【为什么需要导数?】
反向传播需要计算损失函数对每个参数的梯度
根据链式法则,需要知道每一步操作的导数
【ReLU的导数】
- 当x > 0时,导数 = 1
- 当x ≤ 0时,导数 = 0
图示:
↑ 导数
1 ──┼────────
│
├────────→ 输入
│
0 ──┘
【代码解释】
(x > 0) 返回一个布尔数组,True在x>0处
.astype(float) 将True转为1.0,False转为0.0
"""
return (x > 0).astype(float)
def softmax(self, x):
"""
Softmax函数 - 将原始分数转换为概率分布
【什么是Softmax?】
Softmax把任意实数向量转换为"概率分布":
- 所有输出值在0到1之间
- 所有输出值加起来等于1
【公式】
softmax(x_i) = exp(x_i) / Σ exp(x_j)
【例子】
输入: [2.0, 1.0, 0.1]
exp后: [7.39, 2.72, 1.11]
总和: 11.22
输出: [0.66, 0.24, 0.10] ← 这就是概率分布!
【数值稳定性处理】
如果x很大,exp(x)会溢出(变成无穷大)
技巧:先减去最大值,不影响结果但避免溢出
因为 softmax(x) = softmax(x - max(x))
【参数和返回值】
- x: 输入数据,形状(n_samples, 10),每行是一个样本的10个类别分数
- 返回: 概率分布,形状(n_samples, 10),每行的和为1
"""
# 减去每行的最大值,保持数值稳定
# keepdims=True保持维度,方便广播
exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
# 除以每行的和,得到概率
return exp_x / np.sum(exp_x, axis=1, keepdims=True)
def forward_propagation(self, X):
"""
前向传播 - 从输入计算输出
【什么是前向传播?】
数据从输入层"向前"流动,经过每一层的计算,最终得到输出
就像水流经过一系列处理器,最后得到结果
【计算流程】
第1步:输入 → 隐藏层1
z1 = X × W1 + b1 (线性变换)
a1 = ReLU(z1) (激活函数)
第2步:隐藏层1 → 隐藏层2
z2 = a1 × W2 + b2 (线性变换)
a2 = ReLU(z2) (激活函数)
第3步:隐藏层2 → 输出
z3 = a2 × W3 + b3 (线性变换)
a3 = Softmax(z3) (转为概率)
【符号说明】
- z: 线性变换的结果(加权求和)
- a: 激活后的结果
- 下标1,2,3表示第几层
【参数和返回值】
- X: 输入数据,形状(n_samples, 784)
n_samples是样本数量,784是每个样本的特征数
- 返回: 输出概率分布,形状(n_samples, 10)
"""
# ==================== 第一层:输入层 → 隐藏层1 ====================
# 线性变换:z1 = X × W1 + b1
# X的形状: (n_samples, 784)
# W1的形状: (784, 50)
# 矩阵乘法结果: (n_samples, 50)
# b1的形状: (1, 50),会自动广播到(n_samples, 50)
self.z1 = np.dot(X, self.params['W1']) + self.params['b1']
# 激活函数:a1 = ReLU(z1)
# 把负数变成0,正数保持不变
self.a1 = self.relu(self.z1)
# ==================== 第二层:隐藏层1 → 隐藏层2 ====================
# 线性变换:z2 = a1 × W2 + b2
# a1的形状: (n_samples, 50)
# W2的形状: (50, 100)
# 结果形状: (n_samples, 100)
self.z2 = np.dot(self.a1, self.params['W2']) + self.params['b2']
# 激活函数:a2 = ReLU(z2)
self.a2 = self.relu(self.z2)
# ==================== 第三层:隐藏层2 → 输出层 ====================
# 线性变换:z3 = a2 × W3 + b3
# a2的形状: (n_samples, 100)
# W3的形状: (100, 10)
# 结果形状: (n_samples, 10)
self.z3 = np.dot(self.a2, self.params['W3']) + self.params['b3']
# Softmax激活:将分数转换为概率分布
# 每个样本的10个输出值加起来等于1
self.a3 = self.softmax(self.z3)
# 返回最终的概率分布
return self.a3
def backward_propagation(self, X, y, learning_rate=0.01):
"""
反向传播 - 使用SGD(随机梯度下降)更新参数
【什么是反向传播?】
反向传播是神经网络的"学习"过程:
1. 计算预测结果与真实答案的"误差"
2. 把误差从输出层"反向"传播到每一层
3. 根据每层的误差,计算如何调整参数
4. 更新参数,让下次预测更准确
【SGD更新公式】
参数_new = 参数_old - 学习率 × 梯度
【链式法则】
反向传播使用微积分的链式法则:
如果 y = f(g(x)),那么 dy/dx = dy/dg × dg/dx
【各符号说明】
- dz: 损失对z的梯度
- dw: 损失对W的梯度
- db: 损失对b的梯度
- 下标1,2,3表示第几层
【参数解释】
- X: 输入数据,形状(n_samples, 784)
- y: 真实标签,形状(n_samples,),值为0-9的整数
- learning_rate: 学习率,控制每次更新的步长
太大可能不稳定,太小学习太慢
"""
# -------------------- 获取样本数量 --------------------
m = X.shape[0] # 样本数量,用于计算平均梯度
# -------------------- 将标签转换为one-hot编码 --------------------
# 什么是one-hot编码?
# 把类别标签转换为向量形式
# 例如:数字3 → [0,0,0,1,0,0,0,0,0,0]
# 只有第3个位置是1,其他都是0
# np.eye(10)创建10×10的单位矩阵,用y索引选取对应行
y_one_hot = np.eye(self.output_size)[y]
# ==================== 输出层的梯度计算 ====================
# 对于交叉熵损失 + Softmax激活,输出层梯度有简洁公式:
# dL/dz3 = a3 - y_one_hot
#
# 如果真实标签是3,y_one_hot在位置3是1
# 如果预测概率a3在位置3接近1,误差就小
# 如果预测概率a3在位置3远离1,误差就大
dz3 = self.a3 - y_one_hot # 形状: (n_samples, 10)
# 计算W3的梯度:dL/dW3 = a2^T × dz3 / m
# a2^T的形状: (100, n_samples)
# dz3的形状: (n_samples, 10)
# 结果形状: (100, 10),与W3形状相同
# 除以m是取平均
dw3 = np.dot(self.a2.T, dz3) / m
# 计算b3的梯度:dL/db3 = sum(dz3) / m
# 在样本维度求和,保持形状(1, 10)
db3 = np.sum(dz3, axis=0, keepdims=True) / m
# ==================== 隐藏层2的梯度计算 ====================
# 误差反向传播:dz2 = dz3 × W3^T × ReLU导数(z2)
#
# dz3 × W3^T 把输出层的误差传回隐藏层2
# 乘以ReLU导数处理激活函数的影响
dz2 = np.dot(dz3, self.params['W3'].T) * self.relu_derivative(self.z2)
# 计算W2的梯度
dw2 = np.dot(self.a1.T, dz2) / m
# 计算b2的梯度
db2 = np.sum(dz2, axis=0, keepdims=True) / m
# ==================== 隐藏层1的梯度计算 ====================
# 继续反向传播误差
dz1 = np.dot(dz2, self.params['W2'].T) * self.relu_derivative(self.z1)
# 计算W1的梯度
dw1 = np.dot(X.T, dz1) / m
# 计算b1的梯度
db1 = np.sum(dz1, axis=0, keepdims=True) / m
# ==================== SGD参数更新 ====================
# 更新公式:参数 = 参数 - 学习率 × 梯度
#
# 为什么是减法?
# 梯度指向损失增加最快的方向
# 我们要让损失减小,所以往梯度的反方向走
#
# 学习率的作用?
# 控制每次走多远
# 太大可能"跨过"最优点
# 太小学习太慢
# 更新第三层参数
self.params['W3'] -= learning_rate * dw3
self.params['b3'] -= learning_rate * db3
# 更新第二层参数
self.params['W2'] -= learning_rate * dw2
self.params['b2'] -= learning_rate * db2
# 更新第一层参数
self.params['W1'] -= learning_rate * dw1
self.params['b1'] -= learning_rate * db1
def compute_loss(self, y_true):
"""
计算交叉熵损失函数
【什么是损失函数?】
损失函数衡量预测结果与真实答案的"差距"
训练的目标就是让损失函数尽可能小
【什么是交叉熵损失?】
交叉熵是分类问题最常用的损失函数
公式:L = -Σ y_true × log(y_pred)
【直觉解释】
- 如果真实标签是3,我们只关心位置3的预测概率
- 如果预测概率接近1,-log(1) ≈ 0,损失小
- 如果预测概率接近0,-log(0) → ∞,损失大
- 这鼓励模型在正确类别上给出高概率
【参数和返回值】
- y_true: 真实标签,形状(n_samples,)
- 返回: 平均损失值(一个标量)
"""
# 将标签转换为one-hot编码
y_one_hot = np.eye(self.output_size)[y_true]
# 数值稳定性处理
# 避免log(0)导致的-inf
# epsilon是一个很小的数
epsilon = 1e-15
# 将预测概率裁剪到[epsilon, 1-epsilon]范围内
a3_clipped = np.clip(self.a3, epsilon, 1. - epsilon)
# 计算交叉熵损失
# y_one_hot * np.log(a3_clipped): 只保留正确类别的log概率
# np.sum(..., axis=1): 对每个样本求和(实际上每个样本只有一项非零)
# np.mean: 对所有样本取平均
loss = -np.mean(np.sum(y_one_hot * np.log(a3_clipped), axis=1))
return loss
def predict(self, X):
"""
预测数字类别
【功能说明】
给定输入图片,返回预测的数字(0-9)
【处理流程】
1. 前向传播得到概率分布
2. 取概率最大的类别作为预测结果
【参数和返回值】
- X: 输入数据,形状(n_samples, 784)
- 返回: 预测类别,形状(n_samples,),每个值是0-9的整数
"""
# 前向传播得到每个类别的概率
probabilities = self.forward_propagation(X)
# np.argmax返回最大值的索引
# axis=1表示在每行中找最大值
return np.argmax(probabilities, axis=1)
def predict_with_confidence(self, X):
"""
预测数字类别及置信度
【功能说明】
除了返回预测结果,还返回模型的"置信度"
置信度就是预测类别的概率
【置信度的意义】
- 置信度高(如0.95):模型很确定
- 置信度低(如0.3):模型不太确定,结果可能不可靠
【参数和返回值】
- X: 输入数据,形状(n_samples, 784)
- 返回: (预测类别数组, 置信度数组)
"""
# 前向传播得到概率分布
probabilities = self.forward_propagation(X)
# 获取预测类别(概率最大的索引)
predictions = np.argmax(probabilities, axis=1)
# 获取置信度(最大概率值)
confidences = np.max(probabilities, axis=1)
return predictions, confidences
def save_parameters(self, file_path):
"""
保存模型参数到文件
【为什么要保存?】
训练需要很长时间,保存参数后:
- 不需要重新训练
- 可以直接加载用于预测
- 可以分享给别人使用
【文件格式】
.npz是NumPy的压缩格式,可以保存多个数组
【参数】
- file_path: 保存文件的路径
"""
np.savez(file_path,
W1=self.params['W1'], b1=self.params['b1'],
W2=self.params['W2'], b2=self.params['b2'],
W3=self.params['W3'], b3=self.params['b3'])
print(f"模型参数已保存到: {file_path}")
def load_parameters(self, file_path):
"""
从文件加载模型参数
【功能说明】
读取之前保存的参数,恢复模型状态
【参数】
- file_path: 参数文件路径
【返回】
- True: 加载成功
- False: 加载失败
"""
try:
# 加载npz文件
loaded_params = np.load(file_path)
# 将加载的参数放入params字典
self.params = {
'W1': loaded_params['W1'],
'b1': loaded_params['b1'],
'W2': loaded_params['W2'],
'b2': loaded_params['b2'],
'W3': loaded_params['W3'],
'b3': loaded_params['b3']
}
print(f"模型参数已从 {file_path} 加载")
return True
except FileNotFoundError:
# 文件不存在
print(f"参数文件 {file_path} 未找到")
return False
except Exception as e:
# 其他错误
print(f"加载参数时出错: {e}")
return False
python
"""
================================================================================
神经网络推理脚本 - predict.py
================================================================================
【文件功能】
这个脚本用于:
1. 加载训练好的模型参数
2. 对新的手写数字图片进行预测
3. 评估模型的整体性能
4. 可视化预测结果
【什么是推理(Inference)?】
推理是使用训练好的模型进行预测的过程:
- 训练阶段:学习参数(需要标签,需要反向传播)
- 推理阶段:使用参数预测(不需要标签,只需前向传播)
打个比方:
- 训练 = 学生学习知识
- 推理 = 学生用学到的知识答题
【推理流程】
┌──────────────────┐
│ 加载模型参数 │ ← 训练好的权重和偏置
└────────┬─────────┘
↓
┌──────────────────┐
│ 加载测试数据 │
└────────┬─────────┘
↓
┌──────────────────┐
│ 前向传播 │ ← 只有这一步,不需要反向传播
└────────┬─────────┘
↓
┌──────────────────┐
│ 获取预测结果 │
└────────┬─────────┘
↓
┌──────────────────┐
│ 输出/可视化 │
└──────────────────┘
================================================================================
"""
# ==================== 导入必要的库 ====================
import numpy as np # NumPy:数值计算库
import pandas as pd # Pandas:数据处理库
import matplotlib.pyplot as plt # Matplotlib:绑图库
from model import NeuralNetwork # 导入神经网络模型类
# ==================== 中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
def load_and_preprocess_data(csv_path):
"""
加载和预处理数据
【函数功能】
读取CSV文件中的手写数字数据,并进行预处理
【与train.py的区别】
这个函数需要处理两种情况:
1. 带标签的数据(有'label'列):用于评估模型
2. 不带标签的数据(没有'label'列):用于真正的预测
【参数】
- csv_path: CSV文件路径
【返回】
- pixels: 归一化后的像素数据
- labels: 标签数据(如果有的话,否则为None)
"""
print("正在加载数据...")
# 读取CSV文件
data = pd.read_csv(csv_path)
# -------------------- 检查是否有标签 --------------------
if 'label' in data.columns:
# 有标签的情况(训练集或带标签的测试集)
labels = data['label'].values
pixels = data.drop('label', axis=1).values
else:
# 没有标签的情况(真正的预测任务)
labels = None
pixels = data.values
# -------------------- 数据归一化 --------------------
# 将像素值从0-255缩放到0-1
pixels = pixels.astype('float32') / 255.0
print(f"数据加载完成: {len(pixels)}个样本")
return pixels, labels
def visualize_sample(pixels, labels=None, index=0, prediction=None, confidence=None):
"""
可视化手写数字样本
【函数功能】
将一维像素数据(784个值)恢复为二维图片(28×28)并显示
【为什么需要可视化?】
1. 检查数据是否正确加载
2. 直观地看到预测结果
3. 分析模型的错误情况
【参数说明】
- pixels: 所有样本的像素数据
- labels: 真实标签(可选)
- index: 要显示的样本索引
- prediction: 模型预测结果(可选)
- confidence: 模型置信度(可选)
"""
# -------------------- 重塑图片 --------------------
# 将784维向量重塑为28×28的图片
# reshape(28, 28)改变数组形状
image = pixels[index].reshape(28, 28)
# -------------------- 创建图表 --------------------
plt.figure(figsize=(6, 6))
# 显示图片
# cmap='gray'使用灰度色彩映射
plt.imshow(image, cmap='gray')
# -------------------- 设置标题 --------------------
if labels is not None and prediction is not None:
# 有真实标签和预测结果:显示对比
title = f'真实: {labels[index]} | 预测: {prediction} | 置信度: {confidence:.3f}'
# 根据预测是否正确设置颜色
color = 'green' if labels[index] == prediction else 'red'
elif prediction is not None:
# 只有预测结果:显示预测
title = f'预测: {prediction} | 置信度: {confidence:.3f}'
color = 'blue'
else:
# 都没有:只显示索引
title = f'样本 {index}'
color = 'black'
plt.title(title, color=color, fontsize=12)
# 隐藏坐标轴(看图片不需要坐标)
plt.axis('off')
# 自动调整布局
plt.tight_layout()
# 显示图表
plt.show()
def evaluate_model(model, X, y, sample_size=1000):
"""
评估模型性能
【函数功能】
在测试数据上评估模型的准确率
并显示详细的预测结果
【评估指标】
准确率(Accuracy) = 预测正确的样本数 / 总样本数
【参数说明】
- model: 训练好的神经网络模型
- X: 测试数据的特征(像素)
- y: 测试数据的标签
- sample_size: 评估时使用的样本数量(默认1000)
【返回】
- accuracy: 模型的准确率
"""
# -------------------- 采样(如果数据太多)--------------------
# 如果数据量很大,随机抽取一部分进行评估
# 这样速度更快,结果也具有代表性
if len(X) > sample_size:
# 随机选择sample_size个不重复的索引
indices = np.random.choice(len(X), sample_size, replace=False)
X_sample = X[indices]
y_sample = y[indices]
else:
X_sample = X
y_sample = y
# -------------------- 批量预测 --------------------
# 使用模型预测所有样本的类别
predictions = model.predict(X_sample)
# -------------------- 计算准确率 --------------------
# predictions == y_sample:创建布尔数组,True表示预测正确
# np.mean():True算1,False算0,平均值就是正确率
accuracy = np.mean(predictions == y_sample)
# -------------------- 打印结果 --------------------
print(f"模型评估结果:")
print(f"样本数量: {len(X_sample)}")
print(f"准确率: {accuracy:.4f} ({accuracy * 100:.2f}%)")
# -------------------- 显示详细预测结果 --------------------
print(f"\n详细预测结果:")
print("索引 | 真实 | 预测 | 置信度 | 状态")
print("-" * 45)
# 显示前10个样本的预测详情
for i in range(min(10, len(X_sample))):
# 获取单个样本的预测结果和置信度
pred, conf = model.predict_with_confidence(X_sample[i:i + 1])
# 判断预测是否正确
status = "正确" if pred[0] == y_sample[i] else "错误"
# 打印详情
print(f"{i:4d} | {y_sample[i]:4d} | {pred[0]:4d} | {conf[0]:.3f} | {status}")
return accuracy
def predict_single_digit(model, pixel_data):
"""
预测单个数字
【函数功能】
对单个手写数字图片进行预测
【参数说明】
- model: 训练好的神经网络模型
- pixel_data: 单个样本的像素数据(784个值或已经是二维的)
【返回】
- prediction: 预测的数字(0-9)
- confidence: 置信度(0-1)
"""
# -------------------- 确保数据形状正确 --------------------
# 模型需要输入形状为(n_samples, 784)
# 如果输入是一维的(784,),需要重塑为(1, 784)
if len(pixel_data) == 784:
pixel_data = pixel_data.reshape(1, -1) # -1表示自动计算
# -------------------- 进行预测 --------------------
prediction, confidence = model.predict_with_confidence(pixel_data)
return prediction[0], confidence[0]
def main():
"""
主推理函数 - 交互式演示程序
【函数功能】
提供一个交互式界面,让用户可以:
1. 评估模型整体性能
2. 查看单个样本的预测
3. 批量预测演示
【流程说明】
1. 加载训练好的模型参数
2. 加载测试数据
3. 进入交互循环,等待用户选择操作
"""
print("=" * 60)
print("手写数字识别 - 推理模式")
print("=" * 60)
# ==================== 第1步:创建模型 ====================
# 创建一个新的神经网络实例
# 此时参数是随机的,需要加载训练好的参数
model = NeuralNetwork()
# ==================== 第2步:加载训练好的参数 ====================
# 参数文件是训练时保存的
param_file = "nn_sample.npz"
# 尝试加载参数
if not model.load_parameters(param_file):
print("无法加载模型参数,请先运行 train.py 进行训练")
return
# ==================== 第3步:加载测试数据 ====================
csv_path = "E:\\实验报告\\深度学习\\课程内容\\data\\D_number\\D_test.csv"
try:
X, y = load_and_preprocess_data(csv_path)
except FileNotFoundError:
print("数据文件未找到")
return
# ==================== 第4步:交互式推理演示 ====================
# 进入一个循环,让用户选择不同的操作
while True:
# -------------------- 显示菜单 --------------------
print(f"\n选择操作:")
print("1. 评估模型整体性能")
print("2. 查看单个样本预测")
print("3. 批量预测演示")
print("4. 退出")
# 获取用户输入
choice = input("请输入选择 (1-4): ").strip()
# -------------------- 处理用户选择 --------------------
if choice == '1':
# 选项1:整体评估
# 在测试集上计算准确率
evaluate_model(model, X, y, sample_size=1000)
elif choice == '2':
# 选项2:单个样本预测
try:
# 获取用户输入的索引
index = int(input("请输入样本索引 (0-{}): ".format(len(X) - 1)))
# 检查索引是否有效
if 0 <= index < len(X):
# 进行预测
prediction, confidence = model.predict_with_confidence(X[index:index + 1])
# 可视化显示
visualize_sample(X, y, index, prediction[0], confidence[0])
# 打印预测详情
print(f"\n预测详情:")
print(f"样本索引: {index}")
print(f"预测数字: {prediction[0]}")
print(f"置信度: {confidence[0]:.3f}")
else:
print("索引超出范围")
except ValueError:
print("请输入有效数字")
elif choice == '3':
# 选项3:批量演示
print(f"\n批量预测演示:")
# 预测前5个样本
for i in range(5):
prediction, confidence = model.predict_with_confidence(X[i:i + 1])
print(f"样本 {i}: 预测={prediction[0]}, 置信度={confidence[0]:.3f}")
elif choice == '4':
# 选项4:退出
print("再见!")
break
else:
# 无效输入
print("无效选择,请重新输入")
# ==================== 程序入口 ====================
# 当直接运行这个脚本时,执行main函数
if __name__ == "__main__":
main()
python
"""
================================================================================
神经网络训练脚本 - train.py(使用SGD随机梯度下降)
================================================================================
【文件功能】
这个脚本用于训练手写数字识别的神经网络模型
使用的优化方法是:SGD(Stochastic Gradient Descent,随机梯度下降)
【什么是训练?】
训练就是让神经网络"学习"的过程:
1. 给网络看很多带标签的数据(比如数字图片和对应的数字)
2. 网络根据数据调整自己的参数(权重和偏置)
3. 调整的目标是让预测越来越准确
【SGD(随机梯度下降)是什么?】
SGD是最经典的神经网络优化算法:
1. 梯度下降(Gradient Descent):
- 想象你站在山上,想下到山谷(最低点)
- 梯度就像指南针,告诉你"最陡峭"的方向
- 你往梯度的反方向走,就能下山
2. "随机"的含义:
- 不用全部数据计算梯度(太慢)
- 每次只用一小批数据(mini-batch)
- 这个小批是"随机"选取的
3. 更新公式:
参数_new = 参数_old - 学习率 × 梯度
【训练流程图】
┌──────────────────┐
│ 加载训练数据 │
└────────┬─────────┘
↓
┌──────────────────┐
│ 分割训练/验证 │
└────────┬─────────┘
↓
┌──────────────────┐
│ 创建神经网络 │
└────────┬─────────┘
↓
┌────────────┐
│ 开始循环训练│←──────────┐
└─────┬──────┘ │
↓ │
┌────────────┐ │
│ 取一批数据 │ │
└─────┬──────┘ │
↓ │
┌────────────┐ │
│ 前向传播 │ │
└─────┬──────┘ │
↓ │
┌────────────┐ │
│ 计算损失 │ │
└─────┬──────┘ │
↓ │
┌────────────┐ │
│ 反向传播 │ │
│ (SGD更新) │ │
└─────┬──────┘ │
↓ │
┌────────────┐ │
│ 还有数据? │──是────────┘
└─────┬──────┘
│否
↓
┌────────────┐
│ 保存模型 │
└────────────┘
================================================================================
"""
# ==================== 导入必要的库 ====================
import numpy as np # NumPy:数值计算库,用于矩阵运算
import pandas as pd # Pandas:数据处理库,用于读取CSV文件
import matplotlib.pyplot as plt # Matplotlib:绑图库,用于可视化
from model import NeuralNetwork # 导入我们定义的神经网络模型
# ==================== 中文显示配置 ====================
# 默认情况下,matplotlib不支持中文
# 这两行代码让图表可以显示中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
def load_and_preprocess_data(csv_path):
"""
加载和预处理训练数据
【函数功能】
1. 从CSV文件读取数据
2. 分离标签(数字0-9)和像素值
3. 将像素值归一化到0-1范围
【为什么要归一化?】
原始像素值范围是0-255
归一化到0-1有以下好处:
- 数值更小,计算更稳定
- 不同特征的尺度一致
- 梯度下降更容易收敛
【参数】
- csv_path: CSV文件的路径
【返回】
- pixels: 归一化后的像素数据,形状(样本数, 784)
- labels: 标签数据,形状(样本数,)
"""
print("正在加载训练数据...")
# -------------------- 读取CSV文件 --------------------
# pd.read_csv自动解析CSV格式
# CSV是"逗号分隔值"格式,每行一个样本
data = pd.read_csv(csv_path)
# -------------------- 分离特征和标签 --------------------
# 第一列是'label'(标签),其他列是像素值
# 提取标签列,转换为NumPy数组
# .values把Pandas Series转换为NumPy array
labels = data['label'].values
# 删除标签列,剩下的就是像素数据
# axis=1表示删除列(axis=0是删除行)
pixels = data.drop('label', axis=1).values
# -------------------- 数据归一化 --------------------
# 原始像素值:0(黑)到255(白)
# 归一化后:0.0 到 1.0
#
# astype('float32'):转换为浮点数类型
# / 255.0:除以最大值进行归一化
pixels = pixels.astype('float32') / 255.0
print(f"数据加载完成: {len(labels)}个样本")
return pixels, labels
def split_data(X, y, test_size=0.2, random_state=42):
"""
分割训练集和验证集
【为什么要分割?】
我们需要两部分数据:
1. 训练集:用来训练模型,调整参数
2. 验证集:用来评估模型,检测是否过拟合
不能用训练数据来评估,因为模型可能只是"记住"了训练数据
而不是真正"学会"了识别数字
【什么是过拟合?】
过拟合就像死记硬背:
- 考试时只会做见过的原题
- 遇到新题就不会了
验证集就是用来检测这种情况的
【参数】
- X: 特征数据(像素值)
- y: 标签数据
- test_size: 验证集比例,默认0.2(20%)
- random_state: 随机种子,保证每次分割结果一致
【返回】
- X_train, X_val: 训练集和验证集的特征
- y_train, y_val: 训练集和验证集的标签
"""
# -------------------- 设置随机种子 --------------------
# 随机种子让随机结果可重复
# 同样的种子会产生同样的"随机"序列
np.random.seed(random_state)
# -------------------- 生成随机索引 --------------------
# np.random.permutation:生成一个打乱顺序的索引数组
# 例如:原来是[0,1,2,3,4],打乱后可能是[3,1,4,0,2]
indices = np.random.permutation(len(X))
# -------------------- 计算分割点 --------------------
# 如果有100个样本,test_size=0.2
# 分割点 = 100 × (1 - 0.2) = 80
# 前80个用于训练,后20个用于验证
split_point = int(len(X) * (1 - test_size))
# -------------------- 分割索引 --------------------
train_indices = indices[:split_point] # 训练集索引
val_indices = indices[split_point:] # 验证集索引
# -------------------- 根据索引获取数据 --------------------
X_train, X_val = X[train_indices], X[val_indices]
y_train, y_val = y[train_indices], y[val_indices]
return X_train, X_val, y_train, y_val
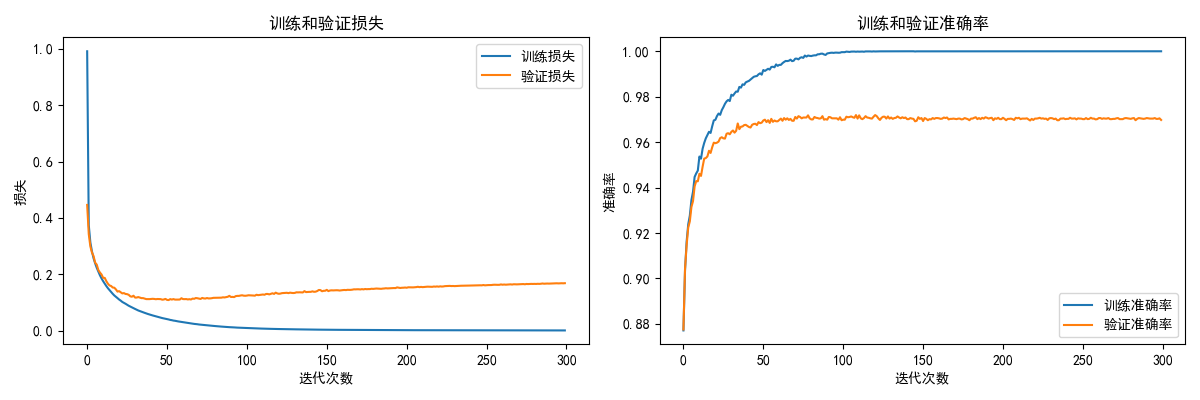
def plot_training_history(history):
"""
绘制训练历史曲线
【函数功能】
可视化训练过程中的损失和准确率变化
通过曲线可以判断:
- 模型是否在学习(损失下降?准确率上升?)
- 是否过拟合(训练好但验证差?)
- 是否需要更多训练(曲线还在下降?)
【参数】
- history: 字典,包含训练过程中记录的数据
- train_loss: 训练损失列表
- val_loss: 验证损失列表
- train_accuracy: 训练准确率列表
- val_accuracy: 验证准确率列表
"""
# 创建画布,包含两个子图
# figsize=(12, 4):宽12英寸,高4英寸
plt.figure(figsize=(12, 4))
# ==================== 第一个子图:损失曲线 ====================
plt.subplot(1, 2, 1) # 1行2列的第1个
# 绘制训练损失曲线
plt.plot(history['train_loss'], label='训练损失')
# 绘制验证损失曲线
plt.plot(history['val_loss'], label='验证损失')
# 设置图表标题和标签
plt.title('训练和验证损失')
plt.xlabel('迭代次数')
plt.ylabel('损失')
# 显示图例
plt.legend()
# ==================== 第二个子图:准确率曲线 ====================
plt.subplot(1, 2, 2) # 1行2列的第2个
# 绘制训练准确率曲线
plt.plot(history['train_accuracy'], label='训练准确率')
# 绘制验证准确率曲线
plt.plot(history['val_accuracy'], label='验证准确率')
# 设置图表标题和标签
plt.title('训练和验证准确率')
plt.xlabel('迭代次数')
plt.ylabel('准确率')
# 显示图例
plt.legend()
# 调整子图间距
plt.tight_layout()
# 保存图片到文件
plt.savefig('training_history.png')
# 显示图表
plt.show()
def train_model():
"""
主训练函数 - 使用SGD优化器
【函数功能】
这是程序的主函数,执行完整的训练流程:
1. 加载数据
2. 数据预处理
3. 创建模型
4. 训练循环
5. 保存模型
【SGD训练流程详解】
对于每个epoch(遍历一次全部数据):
对于每个mini-batch(一小批数据):
1. 前向传播:输入 → 预测
2. 计算损失:预测和真实值的差距
3. 反向传播:计算梯度
4. SGD更新:参数 = 参数 - 学习率 × 梯度
"""
print("=" * 60)
print("开始训练手写数字识别模型(SGD优化器)")
print("=" * 60)
# ==================== 第1步:加载数据 ====================
# 设置数据文件路径
csv_path = "E:\\实验报告\\深度学习\\课程内容\\data\\D_number\\D_train.csv"
try:
# 调用数据加载函数
X, y = load_and_preprocess_data(csv_path)
except FileNotFoundError:
print("数据文件未找到,请检查路径")
return
# ==================== 第2步:分割数据集 ====================
# 80%用于训练,20%用于验证
X_train, X_val, y_train, y_val = split_data(X, y, test_size=0.2)
print(f"训练集: {X_train.shape[0]} 个样本")
print(f"验证集: {X_val.shape[0]} 个样本")
# ==================== 第3步:创建模型 ====================
# 实例化神经网络类
# 参数含义:
# - input_size=784: 输入是28×28=784像素
# - hidden1_size=50: 第一隐藏层50个神经元
# - hidden2_size=100: 第二隐藏层100个神经元
# - output_size=10: 输出是10个类别(0-9)
model = NeuralNetwork(
input_size=784,
hidden1_size=50,
hidden2_size=100,
output_size=10
)
# ==================== 第4步:设置训练参数 ====================
#
# 【epochs(迭代次数/轮数)】
# 一个epoch = 用全部训练数据训练一遍
# 300个epoch意味着模型会看到每个样本300次
epochs = 300
# 【learning_rate(学习率)】
# 控制每次参数更新的步长
# 太大:可能不稳定,跳过最优解
# 太小:学习太慢
# 0.01是常用的初始值
learning_rate = 0.01
# 【batch_size(批次大小)】
# 每次用多少样本计算梯度
# 32是常用的batch size
# 太大:内存占用高,更新次数少
# 太小:梯度估计不准确,训练不稳定
batch_size = 32
# ==================== 第5步:初始化训练历史记录 ====================
# 用字典存储每个epoch的训练指标
# 后续用于绘制训练曲线
history = {
'train_loss': [], # 训练损失
'val_loss': [], # 验证损失
'train_accuracy': [], # 训练准确率
'val_accuracy': [] # 验证准确率
}
# 打印训练配置
print(f"\n训练参数:")
print(f"迭代次数(epochs): {epochs}")
print(f"学习率(learning_rate): {learning_rate}")
print(f"批次大小(batch_size): {batch_size}")
print(f"优化器: SGD(随机梯度下降)")
print("\n开始训练...")
# ==================== 第6步:训练循环 ====================
# 外层循环:每个epoch遍历一次全部数据
for epoch in range(epochs):
# -------------------- 打乱数据顺序 --------------------
# 每个epoch开始时随机打乱数据
# 这样每次epoch中的mini-batch组成都不同
# 有助于模型泛化,减少过拟合
indices = np.random.permutation(len(X_train))
X_train_shuffled = X_train[indices]
y_train_shuffled = y_train[indices]
# 初始化本epoch的损失累加器
total_loss = 0
total_batches = 0
# -------------------- 批次训练(Mini-batch SGD核心部分)--------------------
# 内层循环:按batch_size切分数据,逐批训练
for i in range(0, len(X_train), batch_size):
# 获取当前批次的数据
# i:i+batch_size 是Python切片,获取从i开始的batch_size个样本
X_batch = X_train_shuffled[i:i + batch_size]
y_batch = y_train_shuffled[i:i + batch_size]
# ---------- SGD第1步:前向传播 ----------
# 将输入数据送入网络,得到预测结果
# 这会计算每一层的输出,存储在model内部
model.forward_propagation(X_batch)
# ---------- SGD第2步:计算损失 ----------
# 计算预测结果与真实标签的差距
batch_loss = model.compute_loss(y_batch)
total_loss += batch_loss
total_batches += 1
# ---------- SGD第3&4步:反向传播+参数更新 ----------
# backward_propagation内部会:
# 1. 计算损失对每个参数的梯度
# 2. 使用SGD公式更新参数:
# 参数 = 参数 - learning_rate × 梯度
model.backward_propagation(X_batch, y_batch, learning_rate)
# -------------------- 计算本epoch的指标 --------------------
# 计算平均训练损失
avg_train_loss = total_loss / total_batches
# 在验证集上评估
# 前向传播得到验证集的预测
model.forward_propagation(X_val)
val_loss = model.compute_loss(y_val)
# 计算训练集和验证集的准确率
# np.mean(predictions == labels) 计算预测正确的比例
train_accuracy = np.mean(model.predict(X_train) == y_train)
val_accuracy = np.mean(model.predict(X_val) == y_val)
# -------------------- 记录历史 --------------------
history['train_loss'].append(avg_train_loss)
history['val_loss'].append(val_loss)
history['train_accuracy'].append(train_accuracy)
history['val_accuracy'].append(val_accuracy)
# -------------------- 打印训练进度 --------------------
# 每10个epoch打印一次,避免输出太多
if (epoch + 1) % 10 == 0:
print(f"Epoch {epoch + 1}/{epochs} | "
f"训练损失: {avg_train_loss:.4f} | "
f"验证损失: {val_loss:.4f} | "
f"验证准确率: {val_accuracy:.4f}")
# ==================== 第7步:绘制训练历史曲线 ====================
plot_training_history(history)
# ==================== 第8步:保存模型参数 ====================
# 将训练好的参数保存到文件
# 下次可以直接加载使用,不需要重新训练
model.save_parameters("nn_sample.npz")
# ==================== 第9步:最终评估 ====================
# 显示最终的训练结果
final_train_accuracy = np.mean(model.predict(X_train) == y_train)
final_val_accuracy = np.mean(model.predict(X_val) == y_val)
print(f"\n最终结果:")
print(f"训练集准确率: {final_train_accuracy:.4f} ({final_train_accuracy * 100:.2f}%)")
print(f"验证集准确率: {final_val_accuracy:.4f} ({final_val_accuracy * 100:.2f}%)")
print(f"训练完成!模型参数已保存为 'nn_sample.npz'")
# ==================== 程序入口 ====================
# 当直接运行这个脚本时,执行train_model函数
# 如果是被其他脚本导入,不会自动执行
if __name__ == "__main__":
train_model()训练结果