人工智能之核心技术 深度学习 第二章 神经网络训练与优化

人工智能之核心技术 深度学习

第二章 神经网络训练与优化

---

文章目录

• [人工智能之核心技术 深度学习](#人工智能之核心技术 深度学习)
• 整体训练过程概览
• • 训练循环伪代码
  • 模型初始化（Initialization）
  • • 常用方法：
  • [一、前向传播（Forward Pass）](#一、前向传播（Forward Pass）)
  • [二、损失函数（Loss Function）](#二、损失函数（Loss Function）)
  • • [2.1 分类任务](#2.1 分类任务)
    • • [（1）交叉熵损失（Cross-Entropy Loss）](#（1）交叉熵损失（Cross-Entropy Loss）)
      • [（2）Focal Loss（解决类别不平衡）](#（2）Focal Loss（解决类别不平衡）)
    • [2.2 回归任务](#2.2 回归任务)
  • 三、优化算法
  • • [3.1 梯度下降家族](#3.1 梯度下降家族)
    • [3.2 自适应优化器（自动调学习率）](#3.2 自适应优化器（自动调学习率）)
    • [3.3 学习率调度（Learning Rate Scheduling）](#3.3 学习率调度（Learning Rate Scheduling）)
  • 四、反向传播算法（Backpropagation）
  • • [4.1 核心原理：链式法则](#4.1 核心原理：链式法则)
    • [4.2 梯度问题与解决方案](#4.2 梯度问题与解决方案)
    • • 权重初始化方法
  • 五、正则化技术（防止过拟合）
  • • [5.1 参数正则化](#5.1 参数正则化)
    • [5.2 随机丢弃技术](#5.2 随机丢弃技术)
    • [5.3 Batch Normalization（BN）](#5.3 Batch Normalization（BN）)
    • [5.4 早停（Early Stopping）](#5.4 早停（Early Stopping）)
  • 六、配套代码实现（完整训练流程）
  • 七、总结图谱
• 资料关注

---

整体训练过程概览

神经网络的训练是一个迭代优化过程 ，其核心是通过反向传播 计算梯度，并利用优化算法 更新参数，以最小化损失函数 。同时，为防止过拟合和数值不稳定，需引入正则化 与稳定技术。

完整的训练流程如下：

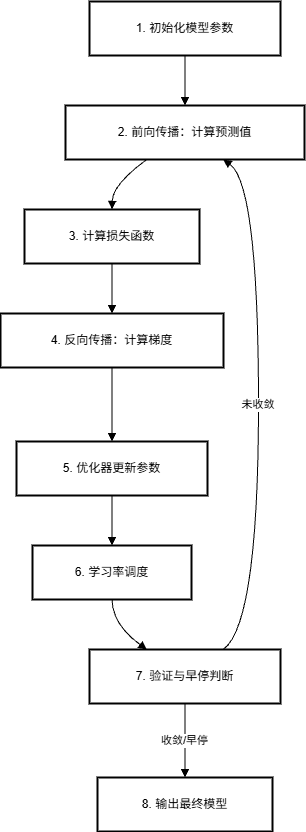
训练循环伪代码

for epoch in range(max_epochs):
    for batch in dataloader:
        # 1. 前向传播
        pred = model(batch.x)
        # 2. 计算损失
        loss = loss_fn(pred, batch.y)
        # 3. 清零梯度
        optimizer.zero_grad()
        # 4. 反向传播
        loss.backward()
        # 5. 梯度裁剪（可选）
        clip_gradients(model)
        # 6. 参数更新
        optimizer.step()
    # 7. 调整学习率
    scheduler.step()
    # 8. 验证 & 早停
    val_loss = evaluate(model, val_loader)
    if early_stop(val_loss): break

✅ 关键思想：

• 前向传播决定"当前做得多差"
• 反向传播 + 优化器决定"如何改进"
• 正则化 + 调度 + 早停确保"学得稳、泛化好"

---

模型初始化（Initialization）

为什么重要？

糟糕的初始化会导致梯度消失/爆炸，使训练无法开始。

常用方法：

激活函数	推荐初始化	原理
ReLU / Leaky ReLU	He 初始化 nn.init.kaiming_normal_(w, mode='fan_in')	保持前向传播方差稳定
Tanh / Sigmoid	Xavier 初始化 nn.init.xavier_uniform_(w)	保持输入输出方差一致

📌 实践建议：现代框架（PyTorch/TensorFlow）默认初始化已较合理，但自定义层时务必注意。

---

一、前向传播（Forward Pass）

• 输入数据通过网络逐层计算：
  a ( l ) = f ( W ( l ) a ( l − 1 ) + b ( l ) ) a^{(l)} = f(W^{(l)} a^{(l-1)} + b^{(l)}) a(l)=f(W(l)a(l−1)+b(l))
• 最终输出用于计算损失。
• 无参数更新，仅用于评估当前模型性能。

---

二、损失函数（Loss Function）

损失函数衡量模型预测值与真实值之间的差距，是训练的"指南针"。

2.1 分类任务

（1）交叉熵损失（Cross-Entropy Loss）

• 适用：多分类（Softmax + CrossEntropy）或二分类（Sigmoid + BCE）
• 公式（二分类） ：
  L = − 1 N ∑ i = 1 N [ y i log ⁡ ( y ^ i ) + ( 1 − y i ) log ⁡ ( 1 − y ^ i ) ] \mathcal{L} = -\frac{1}{N} \sum_{i=1}^N \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] L=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]
• 优点：梯度平滑、对错误预测惩罚大
• PyTorch 实现 ：nn.BCELoss()（需先 Sigmoid）、nn.CrossEntropyLoss()（内部含 Softmax）

（2）Focal Loss（解决类别不平衡）

• 动机：当正负样本极度不均衡时（如目标检测中背景 vs 目标），标准交叉熵会让模型"偷懒"只学多数类。

• 公式 ：
  L focal = − α t ( 1 − p t ) γ log ⁡ ( p t ) \mathcal{L}_{\text{focal}} = -\alpha_t (1 - p_t)^\gamma \log(p_t) Lfocal=−αt(1−pt)γlog(pt)

  • p t p_t pt：正确类别的预测概率
  • γ \gamma γ：聚焦参数（越大，越忽略易分样本）
  • α t \alpha_t αt：类别权重

• 效果：让模型更关注"难分样本"

✅ 选择原则：

• 均衡数据 → 交叉熵
• 极度不平衡（如医学图像、目标检测）→ Focal Loss

---

2.2 回归任务

损失函数	公式	特点	适用场景
MSE（均方误差）	1 N ∑ ( y − y ^ ) 2 \frac{1}{N}\sum (y - \hat{y})^2 N1∑(y−y^)2	对异常值敏感	数据干净、误差小
MAE（平均绝对误差）	1 N ∑ ∣ y − y ^ ∣ \frac{1}{N}\sum |y - \hat{y}| N1∑∣y−y^∣	鲁棒性强	含噪声/异常值
Huber Loss	分段函数：若 ∣ e ∣ ≤ δ |e| \leq \delta ∣e∣≤δ，用 MSE；否则用 MAE	平衡 MSE 与 MAE	通用回归任务

分类
是
否
回归
少
多
任务类型
类别是否平衡?
交叉熵
Focal Loss
数据是否有异常值?
MSE
MAE 或 Huber

---

三、优化算法

目标：通过调整参数 θ \theta θ 最小化损失 L ( θ ) \mathcal{L}(\theta) L(θ)

3.1 梯度下降家族

算法	核心思想	优缺点
SGD（随机梯度下降）	单样本更新： θ ← θ − η ∇ L i \theta \leftarrow \theta - \eta \nabla \mathcal{L}_i θ←θ−η∇Li	噪声大、收敛慢
Mini-Batch SGD	小批量（32~512）平均梯度	平衡效率与稳定性（最常用）
Momentum	引入"惯性"： v = β v + η ∇ L v = \beta v + \eta \nabla \mathcal{L} v=βv+η∇L θ ← θ − v \theta \leftarrow \theta - v θ←θ−v	加速收敛、减少震荡
Nesterov Momentum	"先看再跳"：用未来位置的梯度修正方向	更智能的动量

3.2 自适应优化器（自动调学习率）

算法	核心机制	特点
Adagrad	累积历史梯度平方，大梯度方向降学习率	适合稀疏数据，但学习率可能过早衰减
RMSprop	指数移动平均历史梯度平方	解决 Adagrad 衰减过快问题
Adam	结合 Momentum + RMSprop：一阶矩（均值）+ 二阶矩（方差）	默认首选，鲁棒性强
AdamW	Adam + 解耦权重衰减	更符合 L2 正则化原意，推荐使用

📌 实践建议：

• 默认用 AdamW（比 Adam 更稳定）
• 学习率初始值：AdamW 常用 1e-3 ~ 5e-4

3.3 学习率调度（Learning Rate Scheduling）

固定学习率易陷入局部最优或震荡。动态调整更高效：

调度策略	描述
Step Decay	每 N 轮 ×0.1
Exponential Decay	指数衰减： η t = η 0 ⋅ γ t \eta_t = \eta_0 \cdot \gamma^t ηt=η0⋅γt
Cosine Annealing	余弦退火：从高到低平滑下降，可配合重启（SGDR）
ReduceLROnPlateau	当验证损失停滞时降低学习率

# PyTorch 示例：余弦退火
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=100)

---

四、反向传播算法（Backpropagation）

4.1 核心原理：链式法则

神经网络是一个复合函数：

L = f ( w 3 ⋅ σ ( w 2 ⋅ σ ( w 1 x + b 1 ) + b 2 ) + b 3 ) \mathcal{L} = f(w_3 \cdot \sigma(w_2 \cdot \sigma(w_1 x + b_1) + b_2) + b_3) L=f(w3⋅σ(w2⋅σ(w1x+b1)+b2)+b3)

求梯度 ∂ L ∂ w 1 \frac{\partial \mathcal{L}}{\partial w_1} ∂w1∂L 需层层回传：

∂ L ∂ w 1 = ∂ L ∂ z 3 ⏟ 输出层 ⋅ ∂ z 3 ∂ a 2 ⏟ 权重 ⋅ ∂ a 2 ∂ z 2 ⏟ 激活导数 ⋅ ∂ z 2 ∂ a 1 ⏟ 权重 ⋅ ∂ a 1 ∂ z 1 ⏟ 激活导数 ⋅ ∂ z 1 ∂ w 1 ⏟ 输入 \frac{\partial \mathcal{L}}{\partial w_1} = \underbrace{\frac{\partial \mathcal{L}}{\partial z_3}}{\text{输出层}} \cdot \underbrace{\frac{\partial z_3}{\partial a_2}}{\text{权重}} \cdot \underbrace{\frac{\partial a_2}{\partial z_2}}{\text{激活导数}} \cdot \underbrace{\frac{\partial z_2}{\partial a_1}}{\text{权重}} \cdot \underbrace{\frac{\partial a_1}{\partial z_1}}{\text{激活导数}} \cdot \underbrace{\frac{\partial z_1}{\partial w_1}}{\text{输入}} ∂w1∂L=输出层 ∂z3∂L⋅权重 ∂a2∂z3⋅激活导数 ∂z2∂a2⋅权重 ∂a1∂z2⋅激活导数 ∂z1∂a1⋅输入 ∂w1∂z1

💡 关键：从输出向输入逐层计算梯度，避免重复计算。

4.2 梯度问题与解决方案

问题	原因	解决方案
梯度消失	深层网络中，Sigmoid/Tanh 导数 < 1，连乘趋近 0	- 使用 ReLU- 权重初始化（Xavier/Glorot）- BatchNorm
梯度爆炸	权重过大，梯度连乘爆炸	- 梯度裁剪（Gradient Clipping）- 合理初始化

权重初始化方法

• Xavier 初始化 ：适用于 Sigmoid/Tanh
  W \\sim \\mathcal{U}\\left(-\\sqrt{\\frac{6}{n_{in}+n_{out}}}, \\sqrt{\\frac{6}{n_{in}+n_{out}}}\\right)
• He 初始化 ：适用于 ReLU
  W \\sim \\mathcal{N}\\left(0, \\sqrt{\\frac{2}{n_{in}}}\\right)

---

五、正则化技术（防止过拟合）

5.1 参数正则化

方法	公式	效果
L1 正则化	\\mathcal{L} + \\lambda \\sum |w_i|	产生稀疏权重（特征选择）
L2 正则化	L + λ ∑ w i 2 \mathcal{L} + \lambda \sum w_i^2 L+λ∑wi2	权重趋向小值，防过拟合

⚠️ 注意：PyTorch 中 weight_decay 参数实现的是 L2 正则化

5.2 随机丢弃技术

方法	原理	使用位置
Dropout	训练时随机将部分神经元输出置 0（如 50%）	全连接层后
DropConnect	随机断开权重连接（而非神经元）	较少使用

# Dropout 示例
nn.Sequential(
    nn.Linear(128, 64),
    nn.ReLU(),
    nn.Dropout(0.5),   # 50% 神经元随机失活
    nn.Linear(64, 10)
)

5.3 Batch Normalization（BN）

原理：对每个 mini-batch 的激活值做标准化：

x ^ = x − μ B σ B 2 + ϵ , y = γ x ^ + β \hat{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}, \quad y = \gamma \hat{x} + \beta x^=σB2+ϵ x−μB,y=γx^+β

• μ B , σ B 2 \mu_B, \sigma_B^2 μB,σB2：batch 均值与方差
• γ , β \gamma, \beta γ,β：可学习的缩放与偏移参数

作用：

• 缓解内部协变量偏移（Internal Covariate Shift）
• 允许更高学习率
• 有一定正则化效果（可减少 Dropout 使用）

🔄 LayerNorm：对单个样本的所有特征做归一化，适用于 RNN/Transformer

5.4 早停（Early Stopping）

• 监控验证集损失
• 当验证损失连续 N 轮不再下降，提前终止训练
• 防止过拟合 + 节省计算资源

---

六、配套代码实现（完整训练流程）

import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim.lr_scheduler import CosineAnnealingLR

# 1. 模型定义（带 Dropout 和 BN）
class Net(nn.Module):
    def __init__(self, input_dim, num_classes):
        super().__init__()
        self.fc1 = nn.Linear(input_dim, 128)
        self.bn1 = nn.BatchNorm1d(128)
        self.fc2 = nn.Linear(128, 64)
        self.dropout = nn.Dropout(0.5)
        self.fc3 = nn.Linear(64, num_classes)

    def forward(self, x):
        x = torch.relu(self.bn1(self.fc1(x)))
        x = self.dropout(torch.relu(self.fc2(x)))
        x = self.fc3(x)
        return x

# 2. 数据（模拟）
X = torch.randn(1000, 10)
y = torch.randint(0, 2, (1000,))

# 3. 设置
model = Net(input_dim=10, num_classes=2)
criterion = nn.CrossEntropyLoss()
optimizer = optim.AdamW(model.parameters(), lr=1e-3, weight_decay=1e-4)
scheduler = CosineAnnealingLR(optimizer, T_max=50)

# 4. 训练循环（含早停）
best_val_loss = float('inf')
patience = 10
trigger_times = 0

for epoch in range(100):
    model.train()
    optimizer.zero_grad()
    pred = model(X)
    loss = criterion(pred, y)
    loss.backward()
    
    # 梯度裁剪（防爆炸）
    torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
    
    optimizer.step()
    scheduler.step()

    # 模拟验证（此处用训练损失代替）
    val_loss = loss.item()
    if val_loss < best_val_loss:
        best_val_loss = val_loss
        trigger_times = 0
    else:
        trigger_times += 1
        if trigger_times >= patience:
            print(f"Early stopping at epoch {epoch}")
            break

print("Training finished.")

---

七、总结图谱

训练目标
损失函数
优化算法
反向传播
正则化
分类: CrossEntropy / Focal
回归: MSE / MAE / Huber
SGD 家族
自适应: AdamW
学习率调度
链式法则
梯度稳定: 初始化 + BN
L1/L2
Dropout
Early Stopping
BatchNorm

✅ 黄金组合推荐：

• 优化器：AdamW
• 学习率：余弦退火 + warmup
• 正则化：Dropout + Weight Decay + Early Stopping
• 归一化：BatchNorm（CNN） / LayerNorm（Transformer）

---

资料关注

公众号：咚咚王

gitee：https://gitee.com/wy18585051844/ai_learning

《Python编程：从入门到实践》

《利用Python进行数据分析》

《算法导论中文第三版》

《概率论与数理统计（第四版） (盛骤) 》

《程序员的数学》

《线性代数应该这样学第3版》

《微积分和数学分析引论》

《（西瓜书）周志华-机器学习》

《TensorFlow机器学习实战指南》

《Sklearn与TensorFlow机器学习实用指南》

《模式识别（第四版）》

《深度学习 deep learning》伊恩·古德费洛著 花书

《Python深度学习第二版(中文版)【纯文本】 (登封大数据 (Francois Choliet)) (Z-Library)》

《深入浅出神经网络与深度学习+(迈克尔·尼尔森（Michael+Nielsen）》

《自然语言处理综论 第2版》

《Natural-Language-Processing-with-PyTorch》

《计算机视觉-算法与应用(中文版)》

《Learning OpenCV 4》

《AIGC：智能创作时代》杜雨+&+张孜铭

《AIGC原理与实践：零基础学大语言模型、扩散模型和多模态模型》

《从零构建大语言模型（中文版）》

《实战AI大模型》

《AI 3.0》