**Hi，大家好，我是半亩花海。**在上节说明了迁移学习的第二类方法：特征选择之后，本文主要将介绍迁移学习的第三类方法------子空间学习(2)------流形学习 。本文重点阐述了++Grassmann流形++ 在特征变换中的应用。流形学习假设高维数据具有低维流形结构，利用++测地线距离++ 度量数据关系。文章详细解析了两种代表性方法：SGF通过中间点构建源域到目标域的测地线路径，但存在参数确定难题；GFK则创新性地采用++核学习方法++解决该问题，并提出多源域选择策略。这些方法为处理跨域数据分布差异提供了有效解决方案。
目录
一、流形学习简介
流形学习自从 2000 年在 Science 上被提出来以后，就成为了机器学习和数据挖掘领域的热门问题。它的基本假设是，现有的数据是从一个高维空间中采样出来的，所以，它具有高维空间中的低维流形结构。流形就是是一种几何对象 (就是我们能想像能观测到的)。通俗点说就是，我们无法从原始的数据表达形式明显看出数据所具有的结构特征，那我把它想像成是处在一个高维空间，在这个高维空间里它是有个形状的。一个很好的例子就是星座。满天星星怎么描述？我们想像它们在一个更高维的宇宙空间里是有形状的，这就有了各自星座，比如织女座、猎户座。流形学习的经典方法有 Isomap、locally linear embedding、 laplacian eigenmap 等
流形空间中的距离度量：两点之间什么最短？在二维上是直线（线段），可在三维呢？ 地球上的两个点的最短距离可不是直线，它是把地球展开成二维平面后画的那条直线。那条线在三维的地球上就是一条曲线。这条曲线就表示了两个点之间的最短距离，我们叫它测地线。更通俗一点，两点之间，测地线最短。在流形学习中，我们遇到测量距离的时候， 更多的时候用的就是这个测地线。在我们要介绍的 GFK 方法中，也是利用了这个测地线距离。比如在下面的图中，从 A 到 C 最短的距离在就是展开后的线段，但是在三维球体上看， 它却是一条曲线。
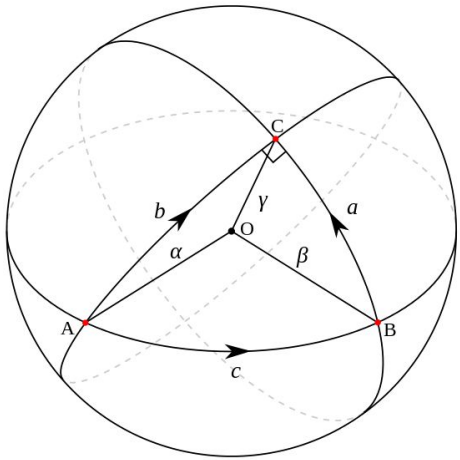图 1：三维空间中两点之间的距离示意图
由于在流形空间中的特征通常都有着很好的几何性质，可以避免特征扭曲，因此我们首先将原始空间下的特征变换到流形空间中。在众多已知的流形中，Grassmann 流形 可以通过将原始的
维子空间 (特征向量) 看作它基础的元素，从而可以帮助学习分类器。在 Grassmann 流形中，特征变换和分布适配通常都有着有效的数值形式，因此在迁移学习问题中可以被很高效地表示和求解 [Hamm and Lee, 2008]。因此，利用 Grassmann 流形空间中来进行迁移学习是可行的。现存有很多方法可以将原始特征变换到流形空间中 [Gopalan et al., 2011, Baktashmotlagh et al., 2014]。
二、SGF方法
在众多的基于流形变换的迁移学习方法中，GFK(Geodesic Flow Kernel) 方法 [Gong et al., 2012] 是最为代表性的一个。GFK 是在 2011 年发表在 ICCV 上的 SGF 方法 [Gopalan et al., 2011] 发展起来的。我们首先介绍 SGF 方法。
SGF 方法从增量学习中得到启发：人类从一个点想到达另一个点，需要从这个点一步一步走到那一个点。那么，如果我们把源域和目标域都分别看成是高维空间中的两个点，由源域变换到目标域的过程不就完成了迁移学习吗？也就是说，路是一步一步走出来的。
于是 SGF 就做了这个事情。它是怎么做的呢？把源域和目标域分别看成高维空间 (即 Grassmann 流形) 中的两个点，在这两个点的测地线距离上取 个中间点，然后依次连接起来。这样，源域和目标域就构成了一条测地线的路径。我们只需要找到合适的每一步的变换，就能从源域变换到目标域了。图 29是 SGF 方法的示意图。
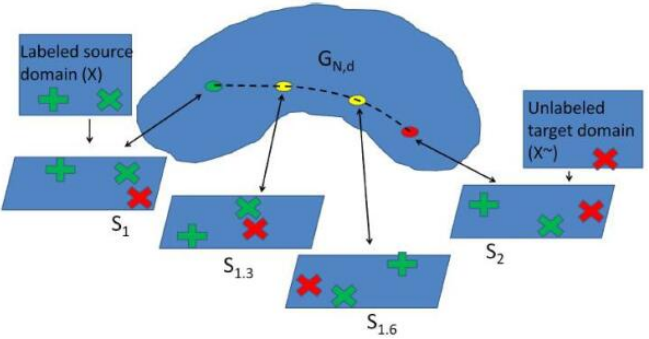图 2：SGF 流形迁移学习方法示意图
SGF 方法的主要贡献在于：提出了这种变换的计算及实现了相应的算法。但是它有很明显的缺点：到底需要找几个中间点？SGF 也没能给出答案，就是说这个参数 d 是没法估计的，没有一个好的方法。这个问题在 GFK 中被回答了。
三、GFK方法 (测地线流式核方法)
GFK 方法 首先解决SGF 的问题：如何确定中间点的个数 。它通过提出一种核学习的方法，利用路径上的无穷个点的积分，把这个问题解决了。这是第一个贡献。然后，它又解决了第二个问题：当有多个源域的时候，我们如何决定使用哪个源域跟目标域进行迁移？GFK 通过提出 Rank of Domain 度量，度量出跟目标域最近的源域，来解决这个问题。图 30 是 GFK 方法的示意图。
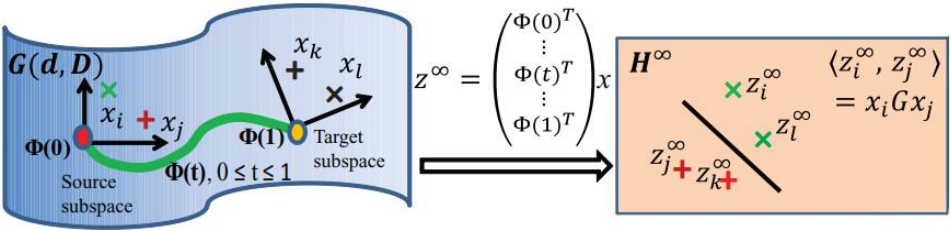图 3：GFK 流形迁移学习方法示意图
用 和
分别表示源域和目标域经过主成分分析 (PCA) 之后的子空间，则
可以视为所有的
维子空间的集合。每一个
维的原始子空间都可以被看作
上的一个点。因 此，在两点之间的测地线
可以在两个子空间之间构成一条路径。如果我 们令
，
，则寻找一条从
到
的测地线就等同于将原始的特征 变换到一个无穷维度的空间中，最终减小域之间的漂移现象。这种方法可以被看作是一种 从
到
的增量式"行走"方法。
特别地，流形空间中的特征可以被表示为 。变换后的特征
和
的内积 定义了一个半正定 (positive semidefinite) 的测地线流式核：
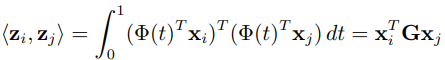
GFK 方法详细的计算过程可以参考原始的文章，我们在这里不再赘述。
四、扩展与小结
子空间学习方法和概率分布自适应方法可以有机地进行组合，克服各自的缺点。下面是一些相关工作。
- DIP (Domain-Invariant Projection) [Baktashmotlagh et al., 2013]：边缘分布自适应 + 流形变换。
-
Baktashmotlagh et al., 2014\]：统计流形法，在黎曼流形上进行距离度量。
五、参考资料
1. 王晋东《迁移学习简明手册》(PDF版) https://www.labxing.com/files/lab_publications/615-1533737180-LiEa0mQe.pdf#page=82&zoom=100,120,392
2. 《迁移学习简明手册》发布啦！ https://zhuanlan.zhihu.com/p/35352154