很多人一看到矩阵乘法就头大,其实它超级亲民------矩阵乘法本质就是一大堆"向量内积"(点积)的组合! 而"矩阵内积"(专业叫Frobenius内积)则是把两个矩阵当成"超级长向量"来点一下,得到一个数字。
咱们一步步来,配大图+例子,保证你看完就彻底懂。
第一部分:先回忆向量内积(点积)------这是所有一切的基础
两个长度一样的向量:
a = [1, 2, 3] b = [4, 5, 6]
内积(点积)就是: 1×4 + 2×5 + 3×6 = 4 + 10 + 18 = 32
几何意义:它等于 a 投影到 b 上的长度 × b 的长度(带方向),或者 |a||b|cosθ。
这就是"内积"最原始的样子。
第二部分:矩阵乘法 = "行 × 列"的内积狂欢
来看最经典的图:
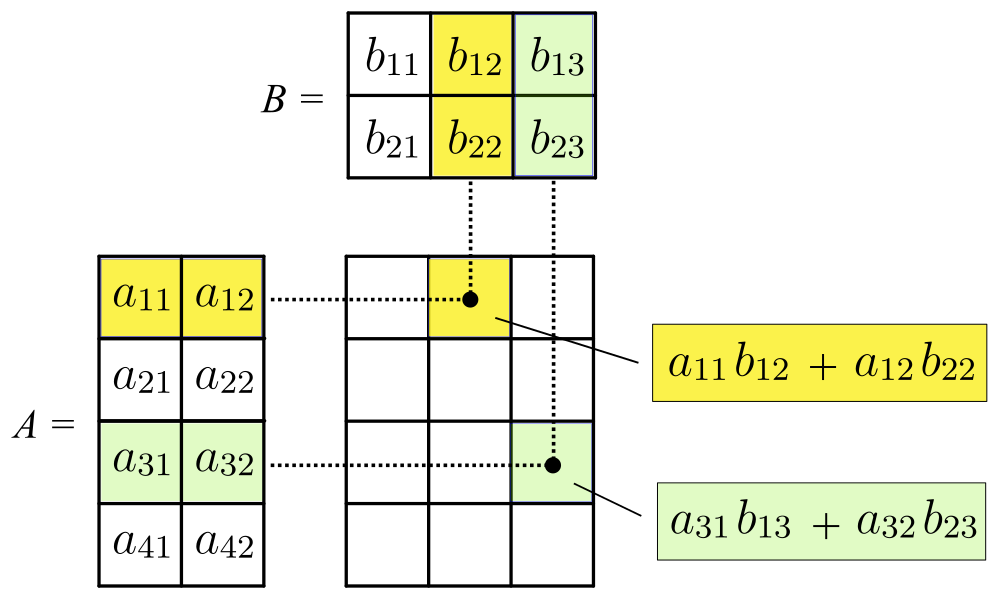
看到没有?
- 左边矩阵的每一行(蓝色高亮)
- 右边矩阵的每一列(绿色高亮)
- 把这一行和这一列对应位置相乘再求和 → 得到结果矩阵的一个数字(黄色位置)
这就是内积!
所以整个矩阵乘法,其实就是:
把左矩阵的所有行,分别和右矩阵的所有列,做向量内积,填满结果矩阵。
下面我用最通俗的方式,把 内积 和 矩阵乘法 讲清楚,并且和图里的黄色/绿色方块一一对应起来。
1)什么是"内积"(点积)?------就是"对应相乘再相加"
先从最简单的 两个向量 说起:
它们的内积(dot product)是:
✅ 通俗理解(像"打分器")
把 x 看成"权重",把 y 看成"数据",那么内积就是:
把每一项按权重加权后汇总成一个总分。
比如:
- 成绩 = (语文权重×语文分) + (数学权重×数学分) + (英语权重×英语分)
2)内积还能表示什么?------"有多同向 / 有多像"
内积还有个非常重要的几何意义:
-
θ 是两向量夹角
-
如果 同方向(θ=0),cosθ=1,内积最大
-
如果 垂直(θ=90),cosθ=0,内积为 0
-
如果 反方向(θ=180),cosθ=−1,内积为负
✅ 所以你可以把内积理解成:
"两个方向有多一致" 的量化指标
3)矩阵乘法到底在干嘛?------"行向量"和"列向量"做内积
关键一句话:
矩阵乘法的每一个结果元素,都是:A 的某一行 和 B 的某一列 的内积。
假设:
-
A 是 m×n
-
B 是 n×p
那么:
C=AB⇒C是 m×p
并且:
cij=(A 的第 i 行)⋅(B 的第 j 列)
也就是:
4)对照你图里的黄色块:这就是在算一个 c1,2
图里:
-
A 是 4×2
-
B 是 2×3
-
所以结果 C=AB 是 4×3
图中黄色是在算结果矩阵里的某个格子(第1行第2列):
A 的第1行(黄色)
B 的第2列(黄色)
它们做内积:
✅ 这就是图右侧黄色框写的那条式子。
5)对照你图里的绿色块:这就是在算另一个 c3,3
绿色是在算结果矩阵里的另一个格子(第3行第3列):
A 的第3行(绿色)
B 的第3列(绿色)
内积:
✅ 这就是图右侧绿色框写的式子。
6)为什么矩阵乘法一定要"行 × 列",而不是"行 × 行"?
因为矩阵乘法的本质是:
把"输入向量"映射成"输出向量"的线性变换。
如果你把 B 看成"输入",那么它的每一列就是一个输入向量:
B=[ 输入1 输入2 输入3 ]
乘上 A 以后:
AB=[ A⋅输入1 A⋅输入2 A⋅输入3 ]
也就是说:
✅ 每一列输入,都会被 A 变换成一列输出
这就解释了为什么要"行和列配对"------维度才能对上,含义也才对。
7)一句话总结(你背下来就通了)
✅ 内积是什么?
对应相乘再相加,得到一个"总分 / 相似度"。
✅ 矩阵乘法是什么?
把 A 的每一行当成"打分器",去给 B 的每一列打分。
每个输出元素,就是一次内积。
我们就用两个 2×2 矩阵,把"矩阵乘法 = 行·列内积"手算一遍。
1)先写清楚矩阵
2)计算 AB:A 的行 去和 B 的列 做内积
结果矩阵也是 2×2:
(1) 左上角 c11 :A 第1行 · B 第1列
A 第1行是 [1,2]
B 第1列是
(2) 右上角 c12 :A 第1行 · B 第2列
B 第2列是
(3) 左下角 c21 :A 第2行 · B 第1列
A 第2行是 [3,4]
(4) 右下角 c22 :A 第2行 · B 第2列
✅ 所以:
3)顺便算一下 BA(你会发现一般不相等)
同样规则:B 的行 · A 的列
左上角:
右上角:
左下角:
右下角:
✅ 所以:
4)关键结论(最重要一句)
矩阵乘法通常不满足交换律,这跟普通乘法不一样。
乘法 vs 内积,一句话区别
| 项目 | 矩阵乘法(A×B) | 矩阵内积(<A,B> 或 A:B) |
|---|---|---|
| 输入要求 | A是m×n,B是n×p | 两个矩阵形状必须完全一样 |
| 输出 | 一个新矩阵(m×p) | 一个数字(标量) |
| 本质 | 每一对"行×列"的向量内积 | 所有"对应位置"的元素内积 |
| 几何/实际意义 | 线性变换的复合(先B后A) | 两个矩阵的"相似程度"(像向量夹角) |
| 常见用途 | 神经网络每一层、3D变换、图像处理 | 机器学习损失函数、正交判断、相似度 |
看完是不是瞬间清楚了?
矩阵乘法看着吓人,其实就是大量小内积的"组团干活"; 矩阵内积则是把整个矩阵当成一个大向量来"亲一口"。
记住那张大蓝绿黄图,你就再也不怕矩阵乘法了!