我爱学算法之—— 回溯

一、子集

题目解析

这道题，给一个nums数组，nums数组中的元素各不相同；

这里要求该数组所有可能的子集（不能包含重复的子集）。

算法思路

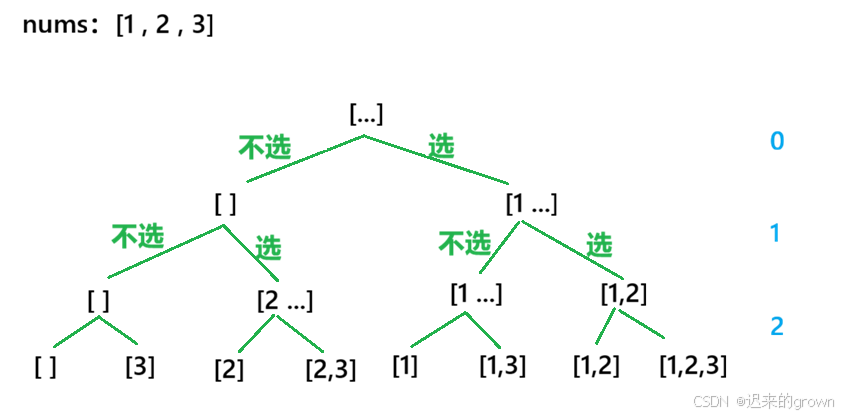
对于这道题，要找出所有可能的子集，就不能像求排列那样，按照每一个位置选择哪一个元素来进行递归选择了；（因为子集中的元素个数是不固定的）

换一个角度想：要求nums的子集，不就是在nums中选择某一些元素吗？

所以，这里就按照nums某个位置的元素存在还是不存在进行递归判断即可；在递归到nums数组末尾时，统计结果即可。

代码实现

cpp 复制代码

class Solution {
    vector<int> path;
    vector<vector<int>> ret;
    void dfs(const vector<int>& nums, int pos) {
        if (pos == nums.size()) {
            ret.push_back(path);
            return;
        }
        // 不选当前位置的元素
        dfs(nums, pos + 1);
        // 选
        path.push_back(nums[pos]);
        dfs(nums, pos + 1);
        path.pop_back(); // 回溯 path
    }
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums, 0);
        return ret;
    }
};

二、找出所有子集的异或总和再求和

题目解析

这道题要求找出nums的所有子集，然后异或再求和；最后返回求和的结果即可。

算法思路

在求nums子集的基础上，再看这道题，可以说是非常简单了；只需统计子集异或的结果即可。

代码实现

cpp 复制代码

class Solution {
    int ret = 0;
    int path = 0;
public:
    void dfs(const vector<int>& nums, int pos) {
        if (pos == nums.size()) {
            ret += path;
            return;
        }
        // 不选pos位置的元素
        dfs(nums, pos + 1);
        // 选pos位置的元素
        path ^= nums[pos];
        dfs(nums, pos + 1);
        // 回溯
        path ^= nums[pos];
    }
    int subsetXORSum(vector<int>& nums) {
        dfs(nums, 0);
        return ret;
    }
};

三、全排列

题目解析

给定一个nums数组，其中不包含重复数字；这里要返回其所有可能的全排列（将nums中随机排列）。

算法思路

对于这道题，要求数组nums的全排列，这里就递归依次选择某一个位置的数字

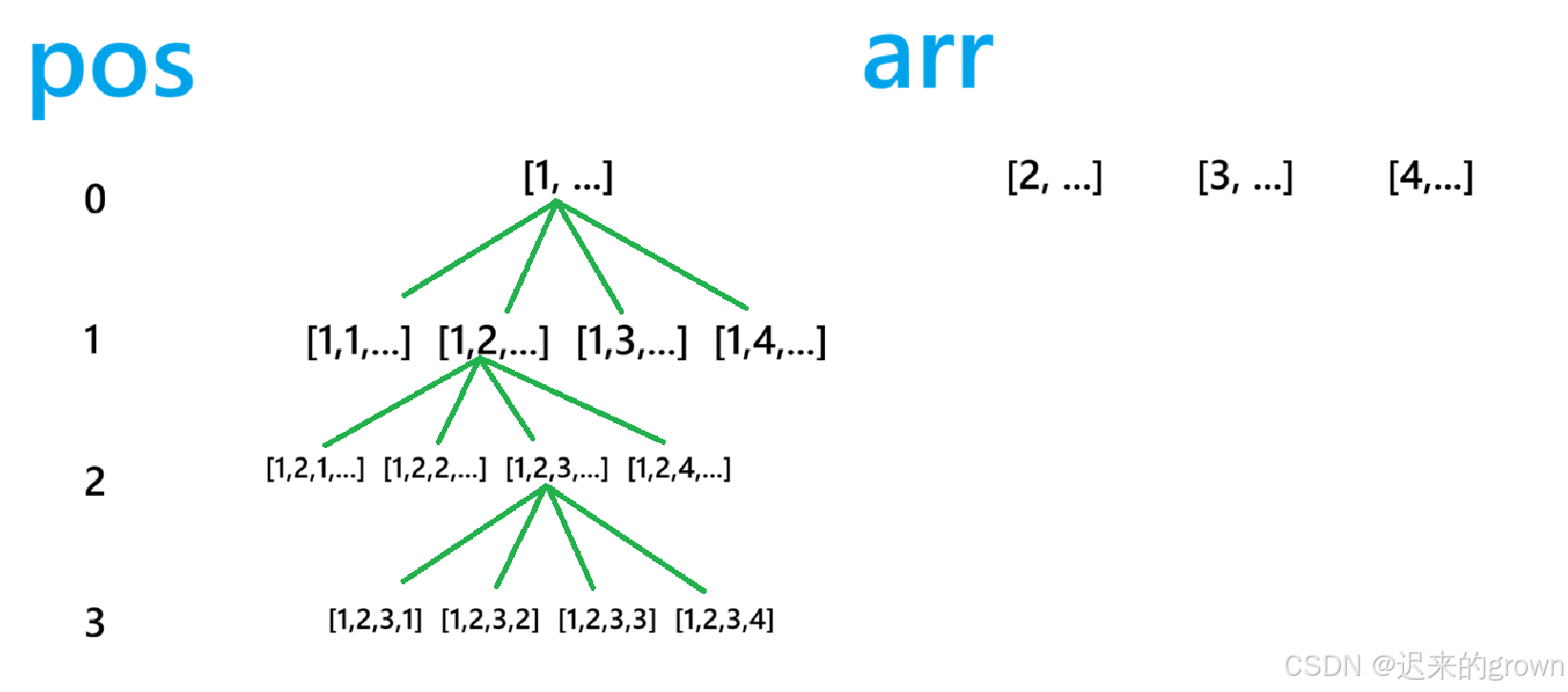
在遍历的过程中，我们可以发现：有很多情况它都是不满足条件的，例如[1,1,...]

在遍历过程中发现，当前分支是不满足条件的，此时就要进行剪枝（简单来说就是不进行后续遍历，返回上级）

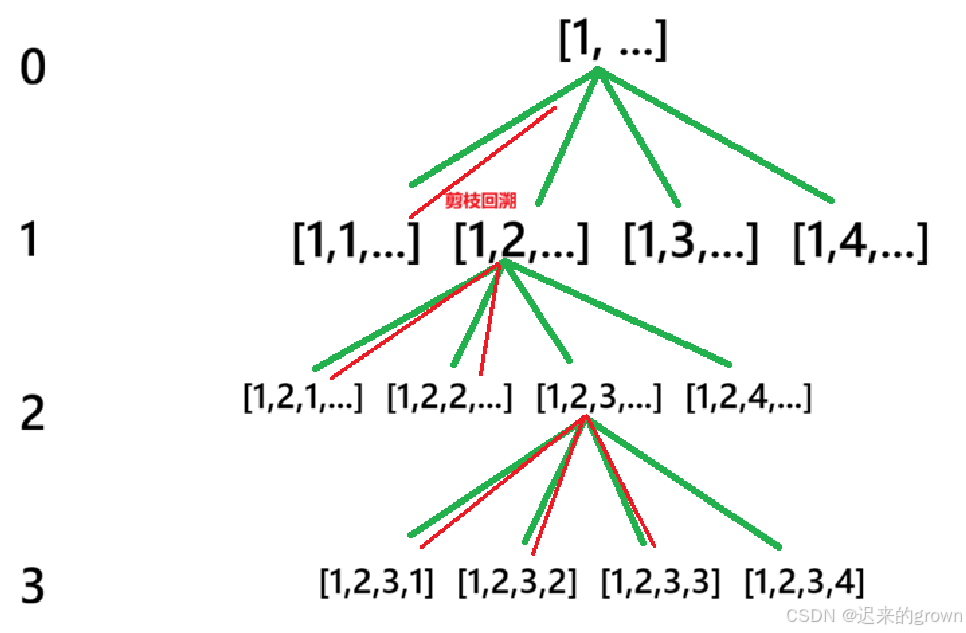
在这道题中，判断是否需要剪枝，只需要判断当前排列中是否存在重复的元素出现即可。

vector<int> arr表示当前排列，bool vis[10]表示nums中所有元素的使用情况（nums中哪个数字出现了），vector<vector<int>> ret 用来记录最终的全排列结果。

回溯

这里就设计到回溯，当遍历到[1,1,..]时，进行剪枝；而当遍历完[1,2..]的所有排列情况后，就要继续遍历[1,3,..]的所有排列情况

所以在递归函数内部，某一分支遍历完之后，就要进行回溯（恢复arr数组）

代码实现

cpp 复制代码

class Solution {
    vector<vector<int>> ret;
    vector<int> arr;
    bool vis[10];

public:
    void dfs(const vector<int>& nums, int pos) {
        if (pos == nums.size()) {
            ret.push_back(arr);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            // 剪枝
            if (vis[i])
                continue;

            vis[i] = true;
            arr.push_back(nums[i]);
            dfs(nums, pos + 1);
            // 回溯
            vis[i] = false;
            arr.pop_back();
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        dfs(nums, 0);
        return ret;
    }
};

四、全排列 II

题目解析

这道题依旧是求数组nums的全排列，唯一的不同就是这里的nums中存在相同的元素，我们要返回所有不重复的全排列。

算法思路

对于这道题，在全排列的基础上，进行去重操作即可。（先找出所有的全排列，然后对结果进行去重，那也太麻烦了）

这里之所以结果中存在相同的全排列，主要就是因为相同的元素，选的顺序（位置）不同导致的

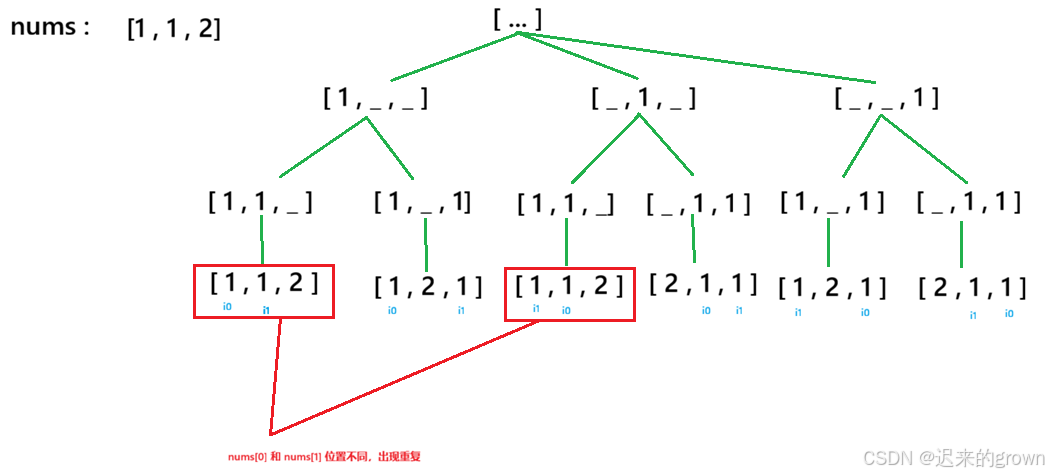
所以，在遍历过程中，只需要避免这种情况出现（剪枝）即可

去重思路：

首先先给nums数组排个序，这样相同的元素都相邻了（保证相同的元素，它们的相对位置不变即可）

其次，在遍历的过程中，记录当前排列中，所有元素是否存在

最后，在判断当前nums[i]是否能够放在当前位置pos时，判断条件（vis[i] == true当前位置元素出现过、或者 i!=0 && nums[i-1] == nums[i] && vis[i-1] == false当前位置前存在相同的数并且前面的数还没出现；此时nums[i]就不能放到pos位置上）

这里只需保证相同元素的相对位置不变，即可达成去重

代码实现

cpp 复制代码

class Solution {
    bool vis[10];
    vector<vector<int>> ret;
    vector<int> path;
public:
    void dfs(vector<int>& nums, int pos) {
        if (pos == nums.size()) {
            ret.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (vis[i] ||
                (i != 0 && nums[i] == nums[i - 1] && vis[i - 1] == false))
                continue;
            vis[i] = true;
            path.push_back(nums[i]);
            dfs(nums, pos + 1);
            // 回溯
            vis[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        dfs(nums, 0);
        return ret;
    }
};

本篇文章到这里就结束了，感谢支持

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws