一、电话号码的字母组合
题目解析
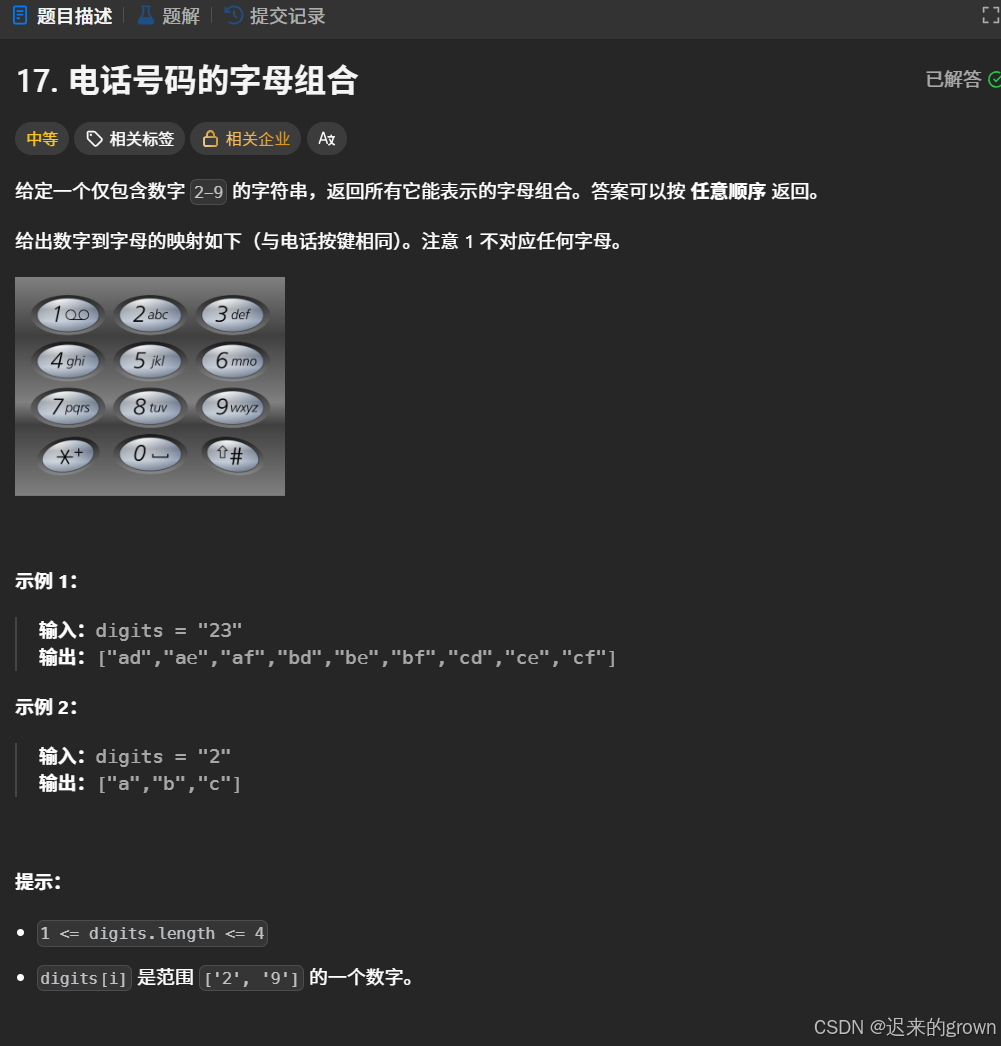
用过9键打字的小伙伴应该非常理解这道题的大致含义;
数字2-9分别对应一些字符串,例如2对应abc、3对应def;当按下数字23时,可能出现的字母组合就有ad、ae、af、bd、be、bf、cd、ce、cf等。
这道题给定应该字符串(其中只包含2-9的数组),要求出所有可能出现的字母组合。
算法思路
这道题整体思路还是非常简单的,根据给定的字符串,依次选择字符即可
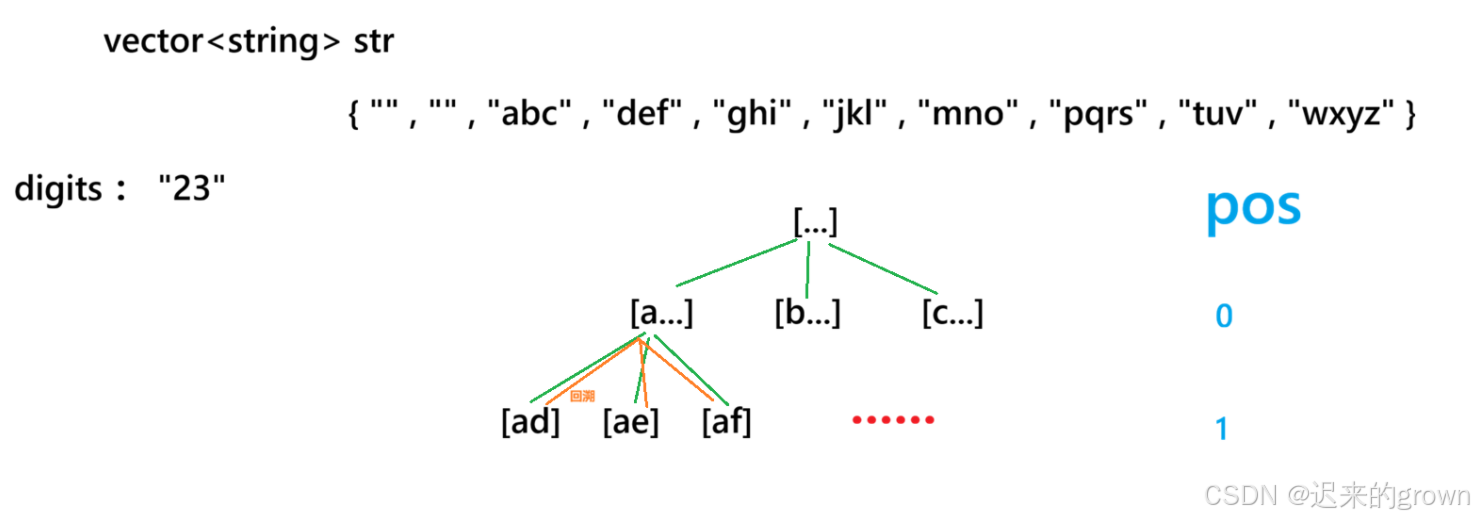
代码实现
cpp
class Solution {
string path;
vector<string> ret;
const vector<string> str = {"", "", "abc", "def", "ghi",
"jkl", "mno", "pqrs", "tuv", "wxyz"};
void dfs(const string& digits, int pos) {
if (pos == digits.size()) {
ret.push_back(path);
return;
}
int num = digits[pos] - '0';
for (int i = 0; i < str[num].size(); i++) {
path.push_back(str[num][i]);
dfs(digits, pos + 1);
path.pop_back();
}
}
public:
vector<string> letterCombinations(string digits)
{
dfs(digits,0);
return ret;
}
};二、括号生成
题目解析
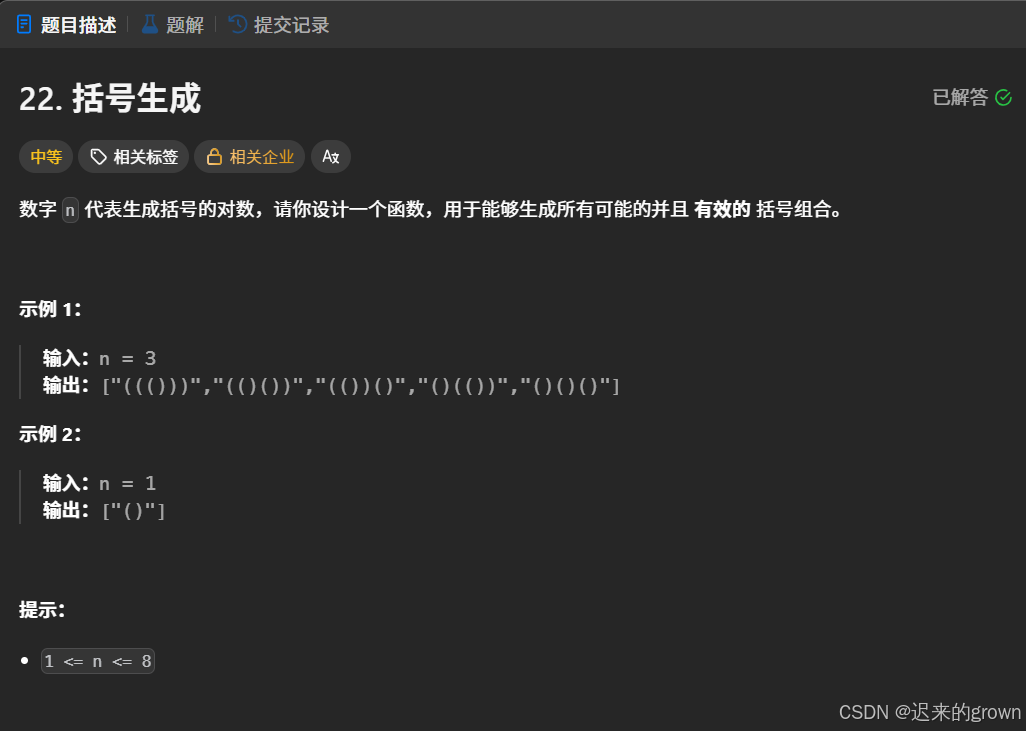
这道题给定一个n,我们要找出所有可能的并且有效的n组括号的组合。(括号有效:)前一定有(与其一一对应------)
算法思路
对于这道题,整体思路:
递归找出 n对括号(2*n个字符),所有的排列情况,然后找出有效的括号组合即可。
找出所有的排列组合情况,再判断有效太麻烦了;就需要在找所有排列组合情况时,进行判断剪枝操作。
剪枝:
有效的括号组合 : 任意
(之前都有)和它一一对应,任意(之后都有)与它一一对应
)之前有(与之对应 : 当前)之前,(的数量一定大于等于)的数量。cnt_left >= cnt_right(算上该()
(之后有)与之对应 : 在最终的排列组合中,(和)的数量相等即可。cnt_left == cnt_right(在)前一定有(与之对应的基础上)
代码实现
cpp
class Solution {
vector<string> ret; // 结果
string path;
int cnt_left = 0; // path 中 ( 数量
int cnt_right = 0; // path 中 ) 数量
public:
void dfs(int n, int pos) {
if (pos == 2 * n) {
if (cnt_left == cnt_right)
ret.push_back(path);
return;
}
// (
cnt_left++;
path.push_back('(');
dfs(n, pos + 1);
// 回溯
cnt_left--;
path.pop_back();
if (cnt_left <= cnt_right)
return; // 剪枝
cnt_right++;
path.push_back(')');
dfs(n, pos + 1);
// 回溯
cnt_right--;
path.pop_back();
}
vector<string> generateParenthesis(int n) {
dfs(n, 0);
return ret;
}
};三、组合
题目解析
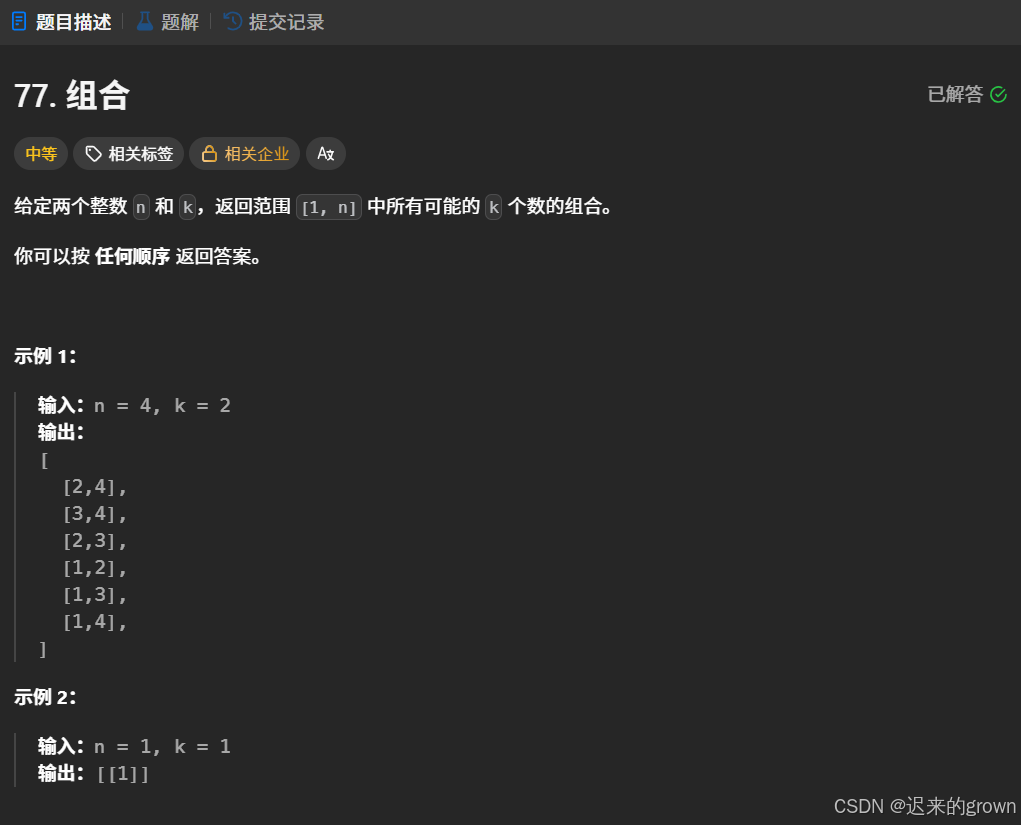
给定两个整数 n 和 k,要求出[1,n]范围中所有可能的k个数的组合
算法思路
对于这道题,可以说丝毫没有难度;(两层for循环遍历,即可)
这里递归实现,dfs的功能就是,找出[begin,n]中所有可能的k个数的组合。
这里之所以是
[begin , n],主要是为了去重(例如[2,3]和[3,2]);这样选择一个数
x之后,在[x,n]中选择其他的数,完成去重操作。
当path,当前选择的数组合的个数等于k时,统计结果即可。
代码实现
cpp
class Solution {
vector<vector<int>> ret;
vector<int> path;
bool vis[22] = {false};
public:
void dfs(int begin, int n, int k) {
if (path.size() == k) {
ret.push_back(path);
return;
}
for (int i = begin; i <= n; i++) {
if (vis[i])
continue;
path.push_back(i);
vis[i] = true;
// 递归
dfs(i+1, n, k);
// 回溯
path.pop_back();
vis[i] = false;
}
}
vector<vector<int>> combine(int n, int k) {
dfs(1, n, k);
return ret;
}
};四、目标和
题目解析
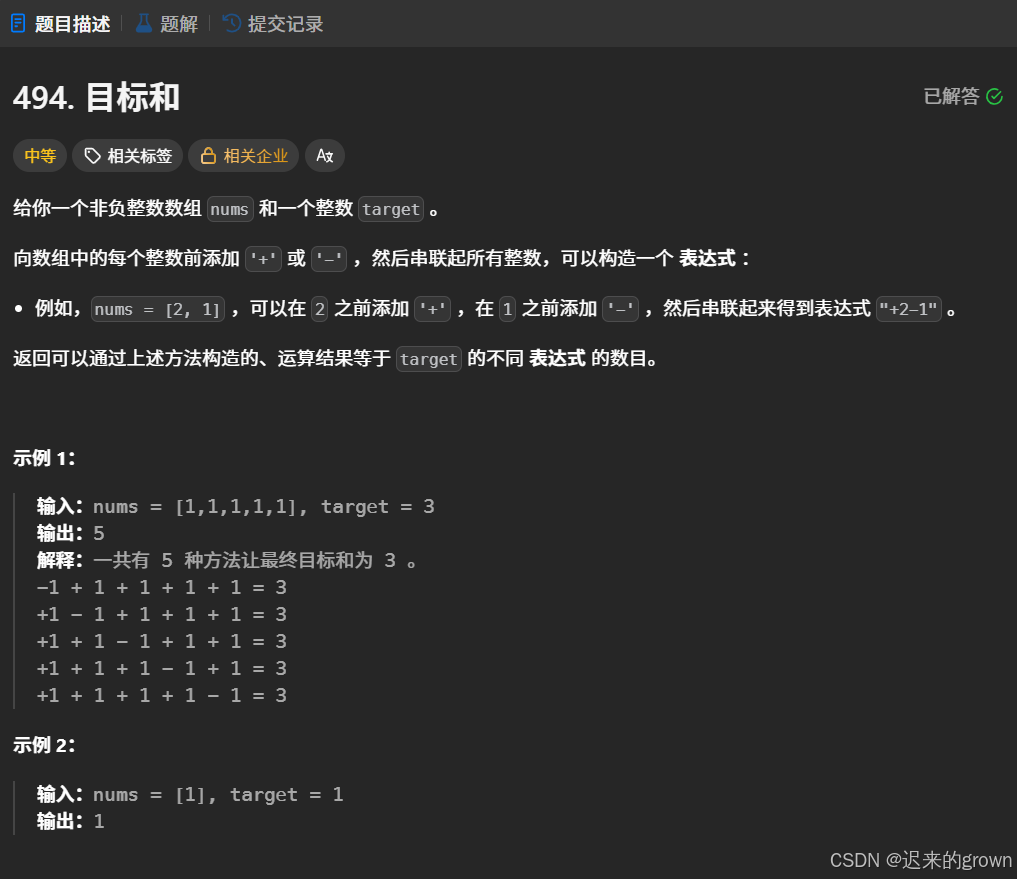
给定一个非负整数数组nums和一个整数target,要求给每一个nums中的元素加上符号(+或-),找出最终和为tarhet的不同表达式的数目。
算法思路
给一个元素加符号,就是+或者-;
这里递归遍历数组nums时为每个元素枚举 +、- 两种符号选择,通过递归深入处理后续元素。递归至数组末尾时,校验当前累加和是否等于目标值,符合则计数加 1。每完成一个符号分支的递归后,回溯恢复累加和状态,最终统计所有有效符号组合的总数。
代码实现
cpp
class Solution {
int ret = 0;
int sum = 0;
public:
void dfs(vector<int>& nums, int target, int pos) {
if (pos == nums.size()) {
if (sum == target)
ret++;
return;
}
// +
sum += nums[pos];
dfs(nums, target, pos + 1);
// 回溯
sum -= nums[pos];
// -
sum -= nums[pos];
dfs(nums, target, pos + 1);
// 回溯
sum += nums[pos];
}
int findTargetSumWays(vector<int>& nums, int target) {
dfs(nums, target, 0);
return ret;
}
};五、组合总和
题目解析
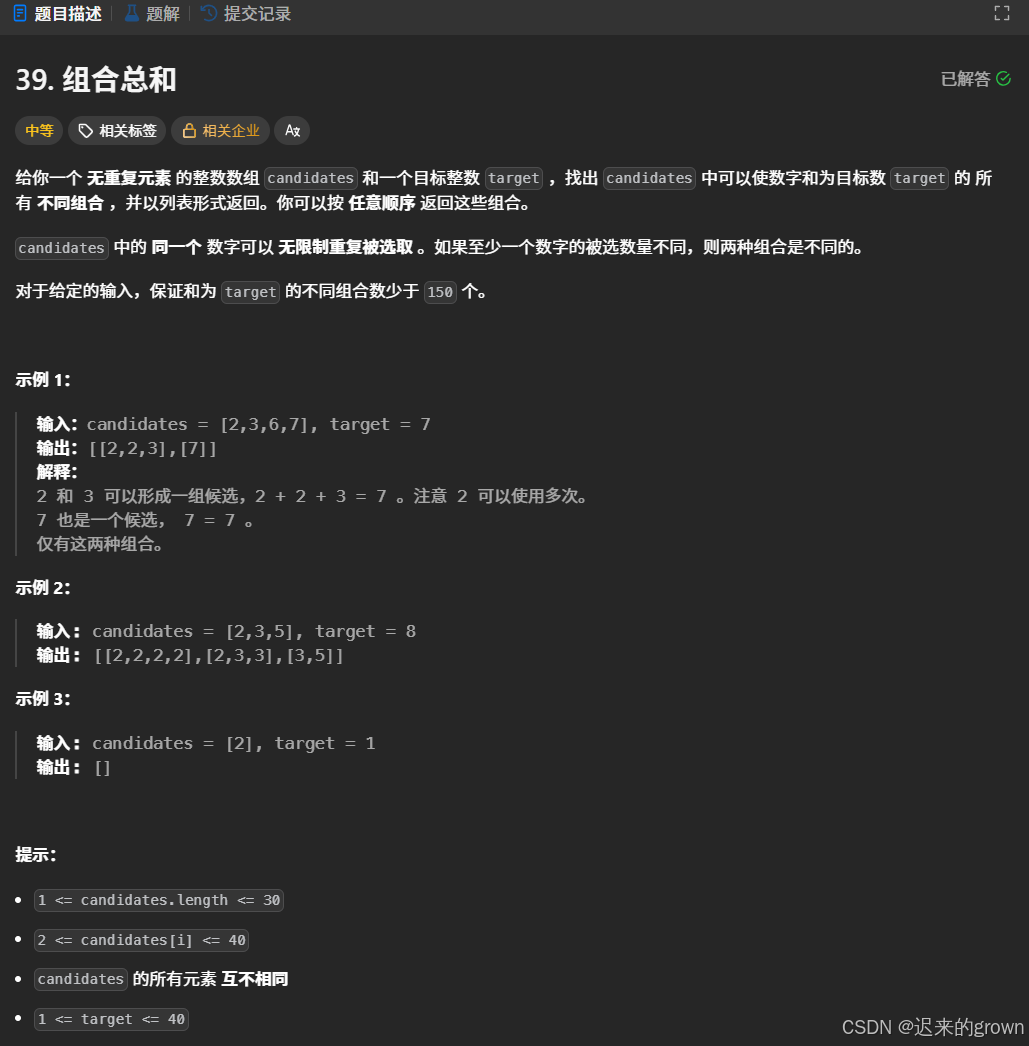
这道题给定一个candidates数组,其中所有元素互不相同,且2 <= candidates[i] <=40;以及一个目标整数target
在candidates中任选元素(可以重复),要求和为target;最终返回所有的不同组合。
算法思路
在上述的递归回溯题目中,都是选择指定数量个元素;而这道题要求我们选择和为target,所以递归结束的判断条件就是和>= target(因为candidates数组中的所有元素都是大于1的)
去重:
最终要返回所有不同的组合,[2,3,3]、[3,2,3]、[3,3,2]这些可以认为都是相同的组合。
这里在递归函数中,就从pos位置之后的选择元素([pos,n])
代码实现
cpp
class Solution {
vector<vector<int>> ret;
vector<int> path;
int sum = 0;
public:
void dfs(vector<int>& candidates,int target,int pos)
{
if(sum == target) ret.push_back(path);
if(sum >= target) return;
for(int i = pos; i< candidates.size();i++)
{
// 选当前位置
sum += candidates[i];
path.push_back(candidates[i]);
dfs(candidates,target,i);
// 回溯
sum -= candidates[i];
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
dfs(candidates,target,0);
return ret;
}
};本篇文章到这里就结束了,感谢支持
我的博客即将同步至腾讯云开发者社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws