Layer Normalization 全解析：LLMs 训练稳定的核心密码

在大语言模型（LLMs）的训练与落地过程中，"梯度消失 / 爆炸""训练不稳定""深层模型难收敛" 是高频痛点。而 Layer Normalization（层归一化，简称 LN）及其变体（RMS Norm、Deep Norm），正是解决这些问题的核心技术 ------ 它们通过标准化网络层的输入分布，让模型参数更新更平稳、收敛更快，同时适配 NLP 任务中变长序列的特性。

本文将从「核心方法原理」「在 LLMs 中的位置差异」「主流模型应用实践」三个维度，系统拆解 Layer Normalization 相关知识，帮你掌握这一 LLMs 基础核心知识点。

一、核心方法篇：从基础 LN 到主流变体

Layer Normalization 的核心思路是对 "单个样本在单个网络层的所有神经元输出" 做标准化（而非 Batch Norm 依赖批次数据），完美适配 NLP 变长序列场景。在此基础上，研究者衍生出 RMS Norm、Deep Norm 等变体，进一步优化性能与效率。

1. 基础款：Layer Norm（层归一化）

1.1 核心计算公式

设某网络层的输出向量为 a=[a1,a2,...,an]（n 为该层神经元数量），Layer Norm 的计算分为 4 步：

计算向量均值
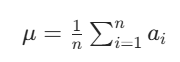
计算向量方差
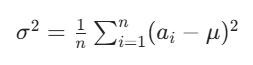
标准化（加入 ϵ 避免分母为 0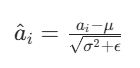）：（ϵ 通常取 10−5，防止方差为 0 导致计算错误）
缩放与平移（保留模型表达能力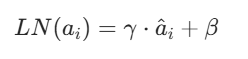）：注：γ（缩放参数）和 β（平移参数）是可学习参数，让归一化后的数据仍能保留层的特征信息。

2. 优化款：RMS Norm（均方根归一化）

RMS Norm 是 LN 的轻量化变体，核心是简化计算、提升效率，同时保证效果。

2.1 核心计算公式

同样设层输出向量为 a=[a1,a2,...,an]，RMS Norm 计算过程：

计算向量的均方根（RMS）：
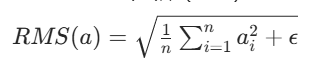
仅做缩放（去除平移步骤）：

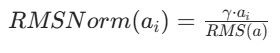
2.2 对比 Layer Norm 的核心特点

计算更高效：去除了 "计算均值 μ" 和 "平移 β" 步骤，减少计算量，训练 / 推理速度更快；
效果持平甚至更优：在多数 LLMs 任务中，RMS Norm 效果与 LN 基本一致，部分场景略有提升；
参数更少：仅需学习缩放参数 γ，无需平移参数 β，降低模型参数量。

3. 深层优化款：Deep Norm

Deep Norm 是针对 "深层 Transformer 训练爆炸" 问题设计的增强型 LN 方案，核心是通过参数缩放稳定训练。

3.1 核心思路

前置操作：在执行 Layer Norm 之前，对残差连接做 "上缩放"（up-scale），即乘以 α（α>1）；
初始化操作：在模型参数初始化阶段，对参数做 "下缩放"（down-scale），即乘以 β（β<1）。

3.2 代码实现（PyTorch 示例）

python

运行

复制代码

import torch
import torch.nn as nn

class DeepNorm(nn.Module):
    def __init__(self, hidden_size, alpha=1.05, beta=0.95, eps=1e-5):
        super().__init__()
        self.alpha = alpha  # 残差连接上缩放系数
        self.beta = beta    # 参数初始化下缩放系数
        self.layer_norm = nn.LayerNorm(hidden_size, eps=eps)
        
    def forward(self, x, residual):
        # 1. 对残差连接做up-scale
        residual_scaled = residual * self.alpha
        # 2. 拼接残差与当前层输出（Transformer残差逻辑）
        h = x + residual_scaled
        # 3. 执行Layer Norm
        h_norm = self.layer_norm(h)
        return h_norm
    
    def init_weights(self, module):
        # 对模型参数做down-scale初始化
        if isinstance(module, (nn.Linear, nn.Embedding)):
            module.weight.data = module.weight.data * self.beta
            if module.bias is not None:
                module.bias.data = module.bias.data * self.beta

3.3 核心优点

限制模型参数的 "爆炸式更新"，将更新幅度约束在常数范围内；
大幅提升深层 Transformer（如千层以上）的训练稳定性，避免梯度失控。

二、位置篇：LN 在 LLMs 中的不同位置差异

LN 在 Transformer 层中的位置直接影响模型训练稳定性和最终效果，主流有 3 种部署方式：

类型	位置特点	核心优势	核心缺点
Post LN	层归一化在残差连接之后	-	深层梯度范式逐渐增大，深层 Transformer 训练易不稳定
Pre-LN	层归一化在残差连接中（输入层之前）	深层梯度范式近似相等，训练更稳定，缓解深层崩溃问题	模型最终效果略差于 Post-LN
Sandwich-LN	Pre-LN 基础上额外插入一个 LN	避免值爆炸问题（Cogview 模型专用）	训练稳定性差，可能导致训练崩溃

关键总结

追求 "训练稳定" 优先选 Pre-LN（主流 LLMs 如 LLaMA、GPT 系列均采用）；
追求 "极致效果" 且模型较浅时可选 Post-LN；
Sandwich-LN 仅为特定场景（如 Cogview 避免值爆炸）设计，通用性差。

三、对比篇：LLMs 中归一化方案的实践选择

不同主流 LLMs 对归一化方案的选择，反映了 "训练稳定性" 与 "模型性能" 的权衡：

BLOOM 模型：在 embedding 层后直接添加 Layer Normalization，核心目标是提升训练稳定性，但会带来一定的性能损失；
LLaMA/LLaMA 2 系列：采用 RMS Norm 替代传统 LN，兼顾效率与效果；
GPT 系列：早期用 Post-LN，后期切换为 Pre-LN + RMS Norm，平衡稳定性与效率；
深层大模型（如千层 Transformer）：采用 Deep Norm 增强 LN，解决深层训练爆炸问题。

核心知识点总结

基础逻辑：Layer Norm 是 LLMs 中适配变长序列的核心归一化方案，通过标准化层输出分布稳定训练；
变体优化：RMS Norm 简化 LN 计算提升效率，Deep Norm 通过参数缩放解决深层训练爆炸问题；
位置选择：Pre-LN 是当前 LLMs 主流选择（稳定优先），Post-LN 效果略优但训练风险高；
实践权衡：模型设计需在 "训练稳定性" 与 "性能 / 效率" 之间取舍（如 BLOOM 牺牲部分性能换稳定）。