从原理到实战：逻辑回归，机器学习的“Hello World”

提到机器学习，很多人会立刻想到复杂的神经网络和各种"高大上"的模型。但今天，我想和你聊聊这个领域里最经典、最基础，同时也最实用的算法之一------逻辑回归（Logistic Regression）。它就像是编程世界里的"Hello World"，是每个机器学习爱好者的必修课。

一、逻辑回归不是回归，是分类！

这可能是最容易让人误解的一点。尽管名字里带着"回归"，但逻辑回归本质上是一个二分类算法。它的任务是根据输入的特征，预测一个样本属于某个类别的概率。

举个例子：

• 银行想根据你的收入、负债等信息，判断你是否会逾期还款（是/否）

• 医生想根据你的体检报告，判断你是否患有某种疾病（患/不患）

• 电商平台想根据你的浏览记录，判断你是否会购买某个商品（买/不买）

这些都是逻辑回归大显身手的场景。

二、核心原理：从线性回归到概率输出

逻辑回归的思想非常巧妙，它在我们熟悉的线性回归基础上，做了一个关键的变换。

第一步：线性预测

逻辑回归首先会像线性回归一样，计算所有输入特征的加权和：
h_\theta(x) = \theta_0 + \theta_1 x_1 + \dots + \theta_n x_n = \theta^T x

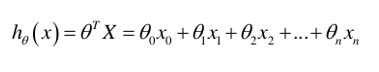
这个值可以是任意大的正数或负数，它本身不具备概率意义。

第二步：Sigmoid函数的魔力

为了把这个连续的预测值转换成我们需要的概率（0到1之间），逻辑回归引入了Sigmoid函数：
g(z) = \frac{1}{1+e^{-z}}

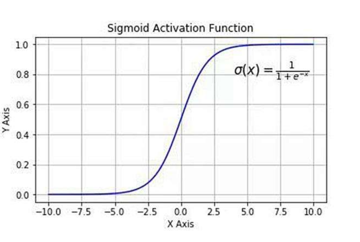
这个函数的图像是一个优美的"S"形曲线，它能把任意实数z映射到(0, 1)区间内。

将第一步得到的线性预测值代入，我们就得到了最终的概率输出：
P(y=1|x;\theta) = \frac{1}{1+e^{-\theta^T x}}

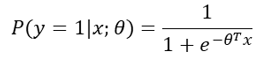
这个公式表示，在给定特征x和模型参数\theta的情况下，样本属于类别1的概率。

三、模型训练：用极大似然估计找到最优参数

我们的目标是找到一组最优的参数\theta，使得模型对训练数据的预测概率最大。这个过程就是极大似然估计（Maximum Likelihood Estimation, MLE）。

简单来说，我们会定义一个"损失函数"来衡量模型预测的好坏，然后通过梯度下降等优化算法，不断调整参数\theta，直到损失函数达到最小值。

四、实战演练：用逻辑回归识别信用卡欺诈

理论说完了，我们来看一个真实的案例。信用卡欺诈检测是金融风控的核心问题，我们用逻辑回归来解决它。

数据预处理

python 复制代码

import pandas as pd
from sklearn.preprocessing import StandardScaler

# 读取数据
data = pd.read_csv("creditcard.csv")
print(data.head())
# 对金额进行标准化
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
# 移除无关特征
data = data.drop(['Time'], axis=1)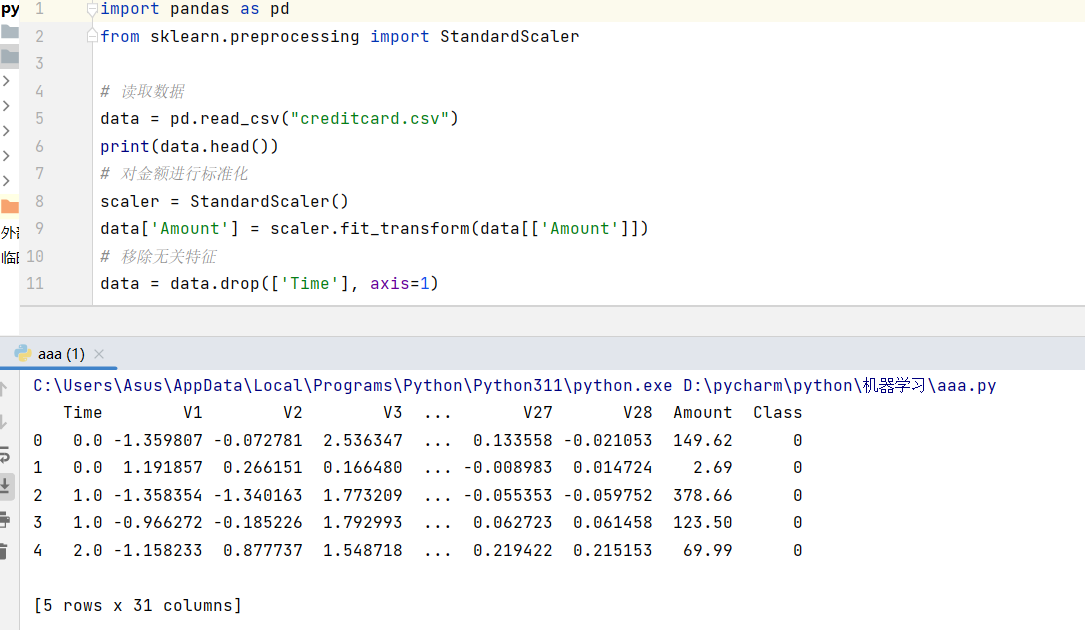

2.绘制图形，查看正负样本

python 复制代码

import matplotlib.pyplot as plt
from pylab import mpl
#matplotlib不能显示中文，借助于pylab实现中文显示
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']#显示中文
mpl.rcParams['axes.unicode_minus'] = False
labels_count =data['Class'] .value_counts()
#统计data['class']中每类的个数
print(labels_count)
plt.title("正负例样本数")  #设置标题
plt.xlabel("类别")        #设置x轴标题
plt.ylabel("频率")
labels_count.plot(kind='bar')
plt.show()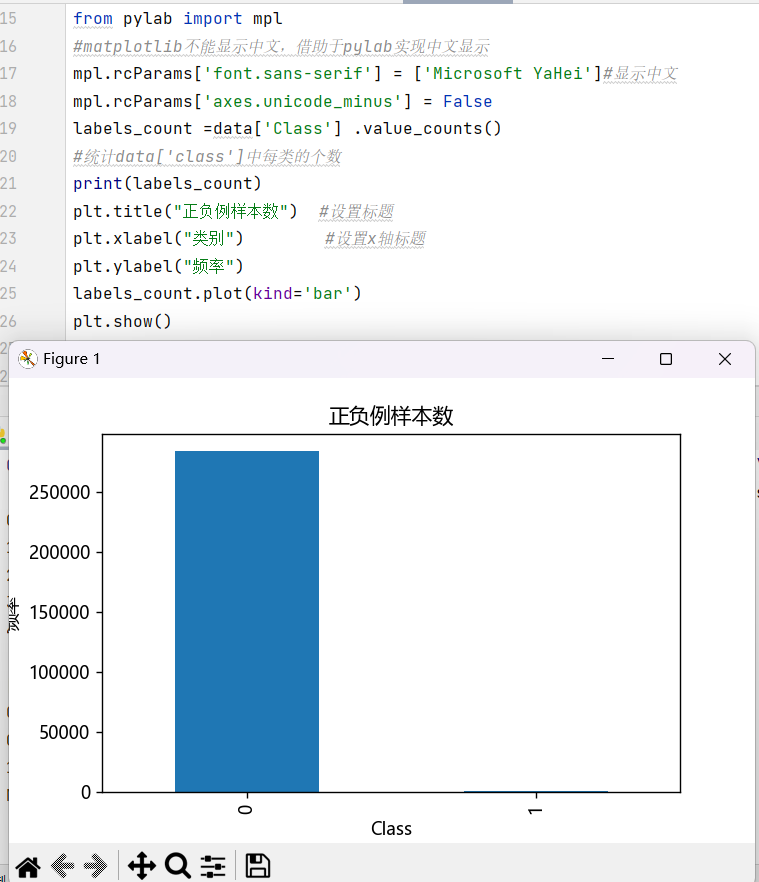

划分数据集

python 复制代码

from sklearn.model_selection import train_test_split

# 分离特征和标签
x = data.drop('Class', axis=1)
y = data['Class']

# 划分训练集和测试集
x_train, x_test, y_train, y_test = \
    train_test_split(x, y, test_size=0.3, random_state=1000)

训练与评估模型

python 复制代码

from sklearn.linear_model import LogisticRegression
from sklearn import metrics

# 初始化并训练模型
lr = LogisticRegression(C=0.01)
lr.fit(x_train, y_train)
# 模型预测
test_predicted = lr.predict(x_test)#测试集
result=lr.score(x_test,y_test)
# 输出评估报告
print(metrics.classification_report(y_test, test_predicted))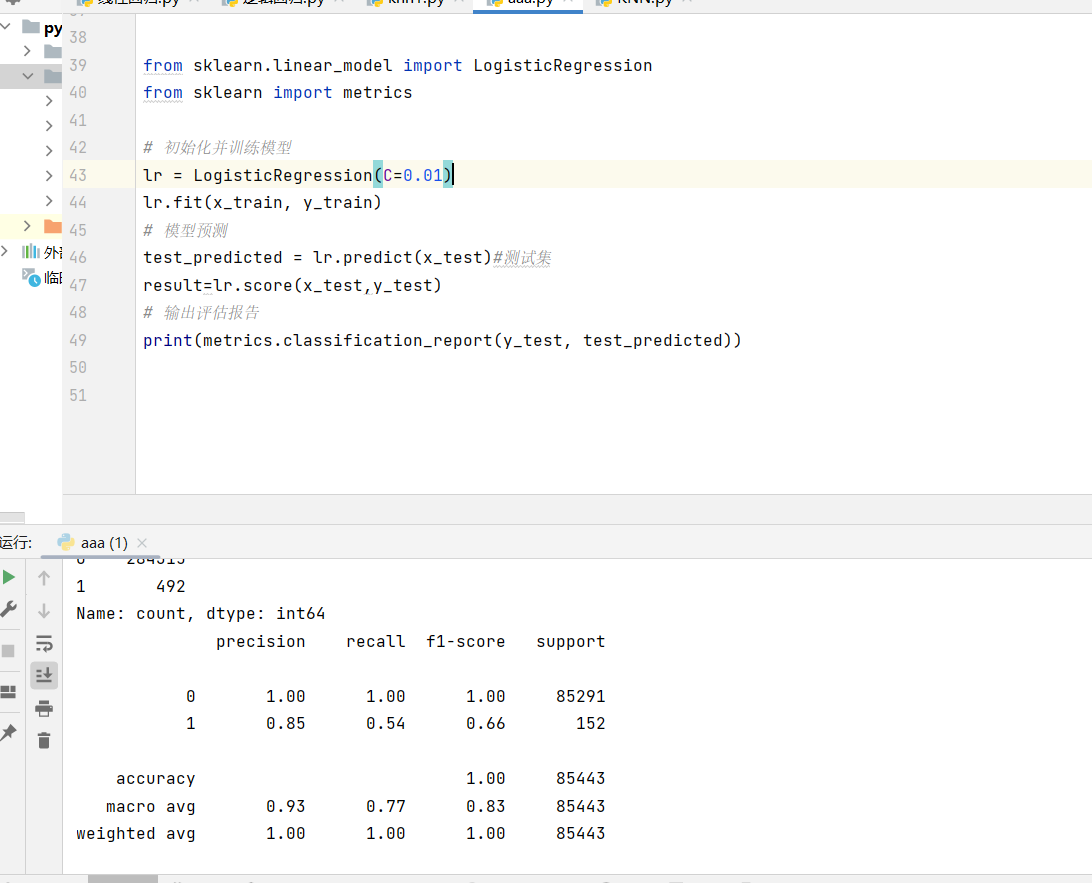

在这个场景里，我们不应该只关注准确率，因为欺诈交易（正例）的数量非常少。我们更需要关注召回率（Recall），它代表了模型能从所有真实欺诈中识别出多少，这直接关系到银行的资金安全。

五、逻辑回归的优缺点

优点

• 简单高效：计算成本低，训练和预测速度都很快。

• 可解释性强：每个特征的系数\theta_i直接反映了该特征对预测结果的影响方向和大小。

• 输出概率：不仅能给出分类结果，还能给出属于该类别的概率，这在很多决策场景中非常重要。

缺点

• 假设性强：假设特征和结果之间存在线性关系，对非线性问题建模能力有限。

• 对异常值敏感：异常值会严重影响模型参数的学习。

• 处理不平衡数据能力弱：在像欺诈检测这样的不平衡数据场景下，需要额外的处理技巧。

六、总结与展望

逻辑回归虽然简单，但它是理解更复杂模型的基石。它背后的思想------用Sigmoid函数将线性预测转化为概率输出，以及用极大似然估计进行参数学习------在很多高级算法中都能找到影子。

掌握了逻辑回归，你就拥有了打开机器学习大门的第一把钥匙。下一步，你可以尝试用它解决更多问题，或者探索如何用特征工程来提升它的性能，甚至可以将它作为基准模型，与更复杂的模型（如随机森林、XGBoost）进行对比。