题目描述
在一个神秘的森林里，住着一个小精灵名叫小蓝。有一天，他偶然发现了一个隐藏在树洞里的宝藏，里面装满了闪烁着美丽光芒的宝石。这些宝石都有着不同的颜色和形状，但最引人注目的是它们各自独特的 "闪亮度" 属性。每颗宝石都有一个与生俱来的特殊能力，可以发出不同强度的闪光。小蓝共找到了 n 枚宝石，第 i 枚宝石的 "闪亮度" 属性值为 Hi，小蓝将会从这 n 枚宝石中选出三枚进行组合，组合之后的精美程度 S 可以用以下公式来衡量：
S=HaHbHc⋅【LCM(Ha,Hb,Hc)/（LCM(Ha,Hb)⋅LCM(Ha,Hc)LCM(Hb,Hc)）】
其中 LCM 表示的是最小公倍数函数。
小蓝想要使得三枚宝石组合后的精美程度 S 尽可能的高，请你帮他找出精美程度最高的方案。如果存在多个方案 S 值相同，优先选择按照 H 值升序排列后字典序最小的方案。
输入格式
第一行一个整数 n 表示宝石个数。
第二行有 n 个整数 H1,H2,...Hn 表示每个宝石的闪亮度。
输出格式
输出一行包含三个整数表示满足条件的三枚宝石的 "闪亮度"。
cs
输入
5
1 2 3 4 9
输出
1 2 3
说明/提示
数据规模与约定
对 30% 的数据，n≤100，Hi≤10^3。
对 60% 的数据，n≤2×10^3。
对全部的测试数据，保证 3≤n≤10^5,1≤Hi≤10^5。
cs
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N 100005//根据题目要求的最大n
int cnt[N]; // 统计每个约数出现的次数，用于记录某个数作为约数出现了多少次
// 比较函数，用于qsort排序
int compare(const void *a, const void *b) {
return (*(int*)a - *(int*)b); // 从小到大排序
}
int main() {
int n;//宝石个数
int x = 1;//最终要找的最大公约数，初始化为1
int c = 0;//计数器，用于输出3个数
scanf("%d", &n);
//h：动态分配数组存储所有宝石闪亮度
int *h = (int*)malloc((n + 1) * sizeof(int));
// 初始化cnt数组
for (int i = 0; i < N; i++) {
cnt[i] = 0;
}
// 读入数据并统计每个数的约数
for (int i = 1; i <= n; i++) {
scanf("%d", &h[i]);
int num = h[i];
// 统计约数
for (int j = 1; j * j <= num; j++) {
if (num % j == 0) {
cnt[j]++; // j是约数
if (j * j != num) {
cnt[num / j]++; // num/j也是约数
}
}
}
}
// 找到出现至少3次的最大约数
for (int i = N - 5; i >= 1; i--) {
if (cnt[i] >= 3) {
x = i; // 这个约数就是最大可能的GCD
break;
}
}
// 对数组排序
qsort(h + 1, n, sizeof(int), compare);
// 输出前3个能被x整除的数
for (int i = 1; i <= n; i++) {
if (h[i] % x == 0) {
printf("%d ", h[i]);
c++;
if (c == 3) {
break;
}
}
}
free(h);
return 0;
}这种有公式的题目，而且公式的所求还不是我们要求的数的时候，有可能只是通过这个公式求一个关系，根据这个关系求所需值
一.整体思路
这段代码的核心思想是：
-
通过约数统计找到三个数可能的最大公约数(最大公约数要尽可能大)
-
选择能被这个最大公约数整除的三个最小数(这三个数要尽可能小)
-
输出这三个数
为什么是这样的思路呢？
根据公式
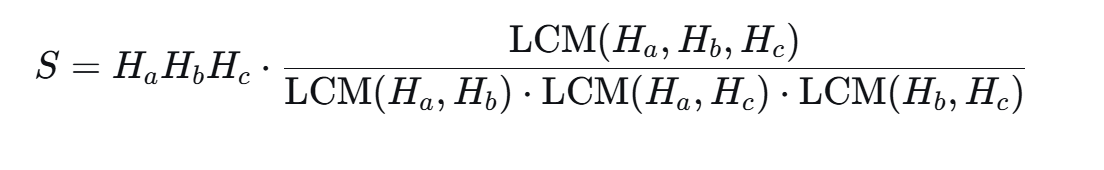
进行公式化简推导，通过化简得到的公式正反比关系，来找到应该怎么寻找最大的s.
设：(在之前最大公约数和最小公倍数题目中解释了为什么x,y,z互质？以及为什么要这么假设)
-
d=GCD(Ha,Hb,Hc)（最大公约数）
-
Ha=d⋅x, Hb=d⋅y, Hc=d⋅z
-
且 GCD(x,y,z)=1（x, y, z互质）
则：
- LCM(Ha,Hb)=d⋅LCM(x,y)
- LCM(Ha,Hc)=d⋅LCM(x,z)
- LCM(Hb,Hc)=d⋅LCM(y,z)
- LCM(Ha,Hb,Hc)=d⋅LCM(x,y,z)
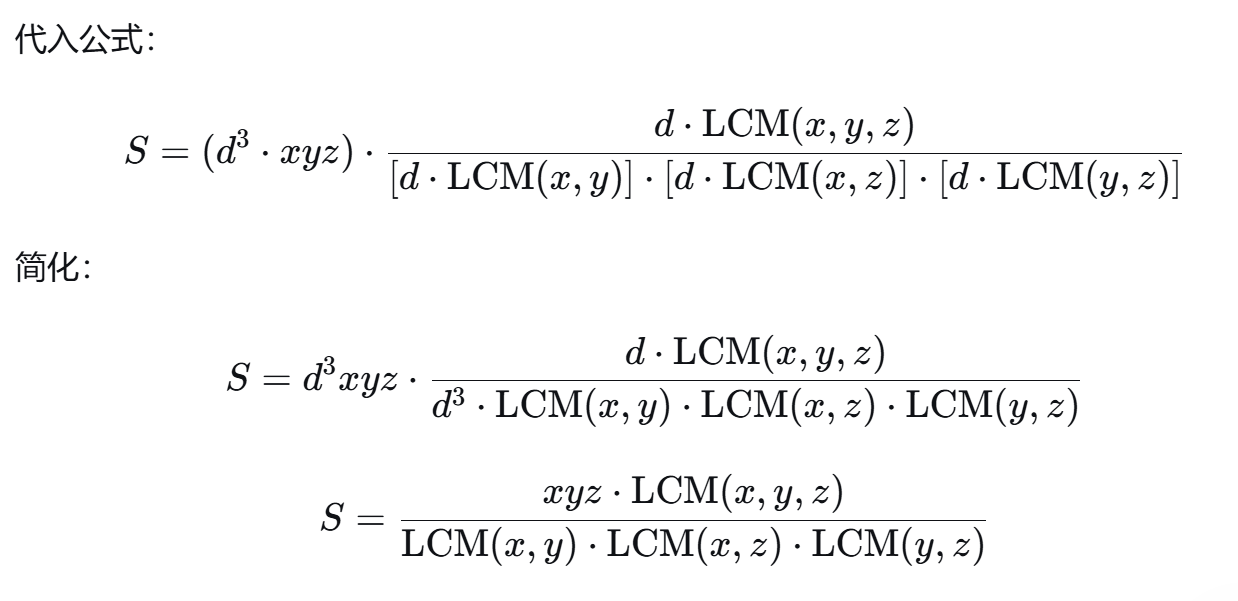
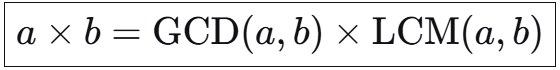根据这个公式，带入到上述公式中可以得到最后关于gcd的关系式。
最后得出结论：S=GCD(X,Y)*GCD(X,Z)*GCD(Y,Z)
所以根据推导得到的公式，发现S与x,y,z之间的关系，因为x, y, z 是 Ha,Hb,Hc 分别除以它们的最大公约数 d 后得到的数，所以可以把d同时乘上，实际上得到的是s与Ha,Hb,Hc之间的关系，只需要得到关系即可，不需要通过这个公式求任何数。得到的关系是只要三个数两两之间的最小公倍数最大，即s最大。又因为题目要求如果很多数的最小公倍数都是这个最大的最小公倍数，就要取最小的三个数。
为什么会出现上述根据假设推导的四个公式？
推导一下：
已知 Ha=d⋅x, Hb=d⋅y
设 g=GCD(x,y)，那么：
- GCD(Ha,Hb)=GCD(d⋅x,d⋅y)=d⋅g
计算：
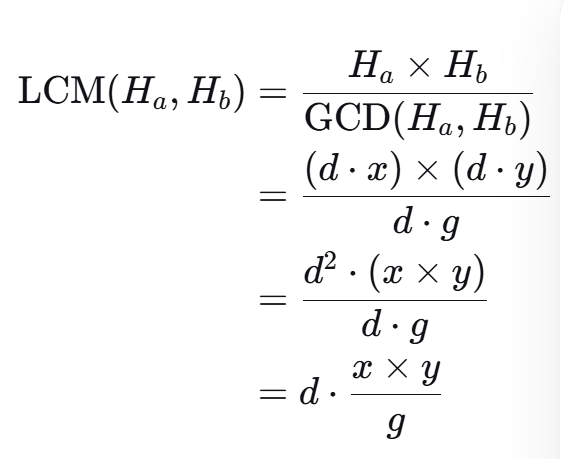
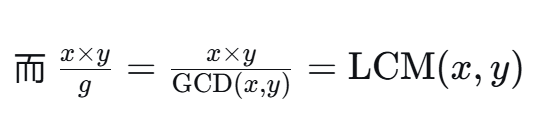
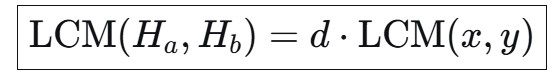
由上图可以类推得到上述三个式子
三个数的最小公倍数：
LCM(A,B,C)=LCM(LCM(A,B),C)
设：
-
Lxy=LCM(x,y)Lxy=LCM(x,y)
-
LHaHb=LCM(Ha,Hb)=d⋅Lxy（由步骤1）
计算：
LCM(Ha,Hb,Hc)=LCM(LHaHb,Hc)=LCM(d⋅Lxy,d⋅z)
这就是上述公式的推导过程。
二.详细解析上述代码：
1.动态内存分配
int *h = (int*)malloc((n + 1) * sizeof(int));//使用malloc后一定要有对应的free，需要手动释放-
(n + 1) * sizeof(int)：计算需要分配的总字节数-
n + 1：需要分配的元素个数 -
sizeof(int)：每个int占用的字节数（通常是4字节）
-
为什么要n+1？
1.后面代码使用：
for (int i = 1; i <= n; i++) {
scanf("%d", &h[i]);
}//从1开始
对比：
-
0-based索引 ：
h[0]到h[n-1]，共n个元素 -
1-based索引 ：
h[1]到h[n]，共n个元素
所以需要分配 n+1 个位置：
-
h[0]位置不使用或作为哨兵 -
h[1]到h[n]存储n个数据
2，防止数组越界
cs
固定数组大小和动态分配数组区别：
1.固定数组大小
#define MAX_N 100000
int h[MAX_N + 1]; // 多分配一个
for (int i = 1; i <= n; i++) {
scanf("%d", &h[i]);
}
2.动态分配数组（分配n个，使用0~based索引）
int *h = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; i++) {
scanf("%d", &h[i]);
}-
malloc((n + 1) * sizeof(int))：向系统申请内存-
malloc：内存分配函数 -
参数：要分配的字节总数
-
返回：指向分配内存起始地址的void指针
-
-
(int*)：类型转换-
将
malloc返回的void*转换为int* -
这样才能用
h[i]这样的数组语法
-
-
int *h = ...：声明指针并初始化-
声明一个整型指针
h -
让它指向刚分配的内存
-
三.四种主要内存分配方式
1.静态分配
cs
#define MAX_N 100000
int arr[MAX_N]; // 全局数组，程序开始就分配
int main() {
static int static_arr[1000]; // 静态局部变量
}特点：
-
编译时确定大小
-
生命周期为整个程序运行期间
-
在数据区（全局/静态区）
有static是静态局部变量：只初始化一次，保持上一次的值
没有static是普通局部变量：每次函数调用都重新初始化，不保持上一次的值，函数返回时自动释放
cs
必须使用static的情况
// 1. 需要计数器保持状态
int get_unique_id() {
static int counter = 0; // 必须static，这样保证下一次调用的时候不会变成初始化的0，而是保存原来的值，不被释放。
return counter++;
}
// 2. 递归中需要共享但不想用全局变量
void dfs() {
static int visited[100][100]; // 所有递归调用共享。结果共享，而不是在其他函数中没有数值存储
// ...
}但几乎不加static，除非特殊要求。
2.栈分配（局部变量）
cs
int main() {
int arr[1000]; // 栈上分配
int n = 100;
int arr2[n]; // 变长数组（VLA），C99
}特点：
-
自动分配和释放
-
大小受栈空间限制（通常1-8MB）
-
速度快
3.堆分配（动态内存）
cs
int *arr = malloc(100000 * sizeof(int)); // 堆上分配
free(arr); // 必须手动释放特点：
-
运行时确定大小
-
需要手动管理
-
空间大，但速度较慢
4.只读常量区
cs
char *str = "Hello"; // 字符串常量开始解答什么时候需要使用动态分配数组？
1.数据大小在运行时才确定
cs
int main() {
int n;
scanf("%d", &n); // 运行时才知道n
// 只能用动态分配
int *arr = malloc(n * sizeof(int));
// 或者 int arr[n];（VLA，但可能栈溢出）
}2.需要大量内存（超过栈限制）但是访问速度慢
cs
int main() {
// int arr[1000000]; // 4MB，可能栈溢出！
int *arr = malloc(1000000 * sizeof(int)); // 堆上，安全
free(arr);
}2.总体思路
首先明确要找的是三个数，这三个数的最大公约数是所有公约数中最大的那个，而这三个数是能被这个最大公约数整除的三个最小的数。
1.步骤一：统计每个数的所有约数
cs
for (int i = 1; i <= n; i++) {
scanf("%d", &h[i]);
int num = h[i];
for (int j = 1; j * j <= num; j++) {
if (num % j == 0) {
cnt[j]++; // j是约数
if (j * j != num) {
cnt[num / j]++; // num/j也是约数
}
}
}
}-
如果
j能整除num，那么：-
j是num的约数，cnt[j]++ -
num/j也是num的约数，cnt[num/j]++ -
注意：当
j*j == num时，只计数一次，避免重复
-
示例 ：num = 12
-
j=1: 12%1=0 →cnt[1]++,cnt[12]++ -
j=2: 12%2=0 →cnt[2]++,cnt[6]++ -
j=3: 12%3=0 →cnt[3]++,cnt[4]++ -
j=4: 4*4>12，循环结束
上述代码找出了num的所有约数。
2.步骤二：找到出现至少3次的最大约数
cs
for (int i = N - 5; i >= 1; i--) {
if (cnt[i] >= 3) {
x = i;
break;
}
}因为要找的这个约数是最大的，所以从最大的开始遍历，只要出现至少3次的约数，就立即结束循环，这个肯定是最大的约数。
3.步骤三：排序并输出结果
cs
// 对数组排序（从小到大）
qsort(h + 1, n, sizeof(int), compare);
// 输出前3个能被x整除的数
for (int i = 1; i <= n; i++) {
if (h[i] % x == 0) {
printf("%d ", h[i]);
c++;
if (c == 3) break;
}
}qsort(h + 1, n, sizeof(int), compare);//C语言标准库中的快速排序函数调用h是指针数组，h+1表示指向h[1]的地址，也就是从h[1]开始排序，跳过h[0].
n表示要排序的元素个数
compare表示比较函数
因为要找的是最大公倍数是x的最小的三个数，所以从1开始进行遍历，只要找到三个最小的数即可结束循环。
四.我自己写的错误的代码：三重循环
cs
#include <stdio.h>
int gcd(int a,int b){
while(b!=0){
int temp=a%b;
a=b;
b=temp;
}
return a;
}
int lcm(int a,int b){
return a/gcd(a,b)*b;
}
int main()
{
int n;
scanf("%d",&n);
int i,j;
int a[100000];
for(i=0;i<n;i++){
scanf("%d",&a[i]);
}
int max=0;
int k;
int b,c,d;
for(i=0;i<n;i++){
for(j=i+1;j<n;j++){
for(k=j+1;k<n;k++){
int m=lcm(a[i],a[j]);
int n=lcm(a[i],a[k]);
int q=lcm(a[j],a[k]);
int o=lcm(a[i]*a[j],a[k]);
int p=o/(m*n*q);
int s=a[i]*a[j]*a[k]*p;
if(s>max){
max=s;
b=i;
c=j;
d=k;
}
}
}
}
printf("%d %d %d",b,c,d);
return 0;
}