文章目录
- [1. 前言](#1. 前言)
- [2. Coursework1](#2. Coursework1)
-
- [2.1 向后传播中 sigmoid 函数里最重要的角色是什么](#2.1 向后传播中 sigmoid 函数里最重要的角色是什么)
- [2.2 什么是 momentum](#2.2 什么是 momentum)
- [2.3 什么是 ReLU](#2.3 什么是 ReLU)
- [2.4 训练集、评估集和测试集之间的对比](#2.4 训练集、评估集和测试集之间的对比)
- [2.5 MLP 和 CNN 的优缺点以及对比](#2.5 MLP 和 CNN 的优缺点以及对比)
- [3. Coursework2](#3. Coursework2)
-
- [3.1 竞争学习的 dead unit 是什么](#3.1 竞争学习的 dead unit 是什么)
- [3.2 LSTM 是什么](#3.2 LSTM 是什么)
- [3.3 RBF](#3.3 RBF)
-
- [3.3.1 RBF函数的基本属性](#3.3.1 RBF函数的基本属性)
- [3.3.2 RBF网络的结构](#3.3.2 RBF网络的结构)
- [3.3.3 RBF怎么确定中心](#3.3.3 RBF怎么确定中心)
- [3.4 有关 Pt.7 的问题](#3.4 有关 Pt.7 的问题)
-
- [3.4.1 时间序列的例子](#3.4.1 时间序列的例子)
- [3.4.2 Elman 网络的结构](#3.4.2 Elman 网络的结构)
- [3.4.3 CEC 的定义](#3.4.3 CEC 的定义)
- [3.5 用神经网络分辨电池](#3.5 用神经网络分辨电池)
-
- [3.5.1 方案](#3.5.1 方案)
- [3.5.2 如何在Matlab里实现(提出一个函数就行)](#3.5.2 如何在Matlab里实现(提出一个函数就行))
1. 前言
首先需要强调的是每年 Coursework 要求不一样,这里分享的是我那一年的 Coursework 情况,并不代表未来也会是这样。大家可以把这篇当作对于自己 INT301 知识的一个回顾,通过这里的问题梳理关键知识点。我会在后面的问题中给出参考答案的同时附带提及它出现在哪里方便能够快速查缺补漏。由于题目是我事后会议的可能有所出入,比如这里的2.1就有所问题,希望大家不要太介意。
整体上来看题目大部分是送分题,会直接考简单的概念,有一些需要你有一定的理解才能打出来,比如对比问题,所以整体 Coursework难度不大,大家不要紧张。
2. Coursework1
2.1 向后传播中 sigmoid 函数里最重要的角色是什么
知识点在 Pt.3 。
首先 sigmoid 函数的定义为 s i g m o i d ( x ) = 1 1 + e − x sigmoid(x) = \frac{1}{1 + e^{-x}} sigmoid(x)=1+e−x1,其导数是 s i g m o i d ′ ( x ) = s i g m o i d ( x ) ∗ ( 1 − s i g m o i d ( x ) ) sigmoid'(x) = sigmoid(x) * (1 - sigmoid(x)) sigmoid′(x)=sigmoid(x)∗(1−sigmoid(x)),因此不需要再额外算指数,非常高效。其的第一个优点是计算简单。
其次是它在向后传递中的作用是用于把误差信号往前一层一层地传。
但是其也存在问题,这就是这节提到的梯度消失问题。sigmoid 的导数决定了误差能传多少回去,但是多层相乘后,梯度会迅速变得极小,前面的层几乎学不到东西。
2.2 什么是 momentum
知识点在 Pt.4。
momentum(动量)是优化算法里一个用来"让梯度更新更稳、更快"的机制。
因此权重更新公式为 Δ w ( t ) = − η ∂ E e ∂ w ( t ) + α Δ w ( t − 1 ) \Delta w(t) = -\eta \frac{\partial E_e}{\partial w(t)} + \alpha \Delta w(t-1) Δw(t)=−η∂w(t)∂Ee+αΔw(t−1)。
其中, Δ w ( t ) Δw(t) Δw(t)是当前权重变化量, η η η是学习率, ∂ E e ∂ w ( t ) \frac{\partial E_e}{\partial w(t)} ∂w(t)∂Ee是损失函数对权重的偏导数(梯度), α α α是动量系数,用于控制前一次权重变化在当前更新中的影响, Δ w ( t − 1 ) Δw(t−1) Δw(t−1)是前一次的权重变化量。
如果 α = 0 α=0 α=0,权重更新完全由梯度下降决定,这就是普通的反向传播。
如果 α = 1 α=1 α=1,梯度下降被完全忽略,权重更新仅基于之前的动量,这可能导致模型无法有效学习。
通常, α α α的值在 0.6 到 0.9 之间。这个范围内的值可以在保持梯度下降的影响的同时,利用动量加速收敛。
2.3 什么是 ReLU
这里在 INT301 没用详细介绍,但是在 INT305 中我们对几种激活函数都有详细的介绍。
首先 ReLU 函数的定义是 R e L U ( x ) = m a x ( 0 , x ) ReLU(x) = max(0, x) ReLU(x)=max(0,x)。
因此其导数在 x > 0 x>0 x>0时是 1 1 1,否则为 0 0 0。
图像如下。
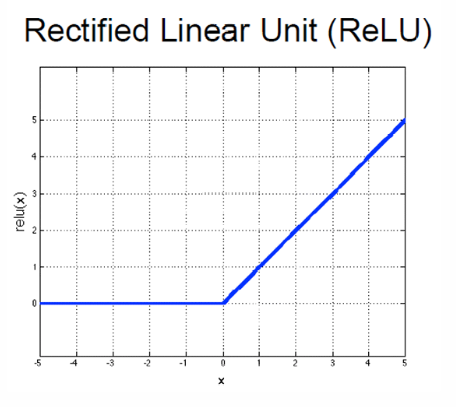
它简单,计算效率高,有助于缓解梯度消失问题,但可能导致"死亡ReLU"问题(即神经元永久失活)。
2.4 训练集、评估集和测试集之间的对比
这里也可以参考INT303里的讲解相关链接。
下面的表格进行了一个大致的对比。
| 数据集 | 是否更新参数 | 是否用于调参 | 是否多次使用 | 作用 |
|---|---|---|---|---|
| 训练集 | 是 | 否 | 多次 | 学习 |
| 评估集 | 否 | 是 | 多次 | 调参 |
| 测试集 | 否 | 否 | 一次 | 最终评估 |
所以训练集用于训练模型参数,验证集用于调整模型和超参数,测试集用于最终评估模型性能。一般他们的比例是8:1:1。
2.5 MLP 和 CNN 的优缺点以及对比
这个就是 Coursework1 中考的较深的了。并不是直接的知识点回答而是涉及到了两个知识点的对比。
相关的知识点可以翻看 MLP 和 CNN 的相关介绍,无论是这门课的还是别的课的,可能 CNN 看 INT305 之类的会更好。
首先简单的对比表如下。
| 维度 | MLP | CNN |
|---|---|---|
| 连接方式 | 全连接 | 局部连接 |
| 参数量 | 很大 | 较小 |
| 空间信息 | 不保留 | 保留 |
| 权重共享 | 否 | 是 |
| 平移不变性 | 无 | 有 |
| 图像任务 | 效果差 | 效果好 |
| 结构复杂度 | 简单 | 较复杂 |
我们这里可以稍微介绍一下 MLP 是由两个全连接层组成,每个神经元连接所有输入,其不关心空间位置。
CNN 是由卷积层、池化层、全连接层组成,其的特点有局部连接(local receptive field)、权重共享(shared weights)、保留空间结构。
因此 MLP 的优点:
- 结构简单,容易理解和实现
- 适合结构化 / 表格数据
- 对输入形式要求低(拉直即可)
缺点:
- 参数量巨大
- 完全忽略空间信息
- 对图像、语音等高维数据效果差
- 容易过拟合
CNN 的优点:
- 参数大幅减少
- 自动提取局部特征
- 平移不变性强
- 图像/语音任务效果极佳
缺点:
- 结构复杂,设计成本高
- 对非空间结构数据不友好
- 需要较多计算资源(GPU)
我们还可以提到它们的核心假设不一样。
MLP 的假设所有输入特征同等重要、独立。
而 CNN 假设局部相关性强。
我们最后还可以比较它们的应用:
MLP 经常用于表格数据、简单的回归/分类问题、小规模特征工程问题。
CNN 用于图像分类/检测、语音信号、视频和医学影像。
3. Coursework2
3.1 竞争学习的 dead unit 是什么
dead unit出现在 Pt.8。
dead unit 是指在竞争学习中,从来没有"赢过竞争",因此权重几乎不再更新的神经元。
3.2 LSTM 是什么
LSTM 出现在 Pt.7。
这里说的 LSTM 知识点其实不够清晰且有冲突,可以参考 INT305 中的介绍(INT305 中的 LSTM)。
LSTM(Long Short-Term Memory)是一种特殊的 RNN,通过门控机制来选择性地记住或遗忘信息,用于建模长期依赖。
LSTM 通过 cell state(细胞状态 c t c_t ct)以更新信息,这其中还包括:
- Forget Gate(遗忘门): f t = s i g m o i d ( W f [ h ( t − 1 ) , x t ] + b f ) f_t = sigmoid(W_f [h_{(t-1)}, x_t] + b_f) ft=sigmoid(Wf[h(t−1),xt]+bf)
决定旧记忆 c ( t − 1 ) c_{(t-1)} c(t−1)保留多少。 - Input Gate(输入门): i t = s i g m o i d ( W i [ h ( t − 1 ) , x t ] + b i ) i_t = sigmoid(W_i [h_{(t-1)}, x_t] + b_i) it=sigmoid(Wi[h(t−1),xt]+bi)
c t = t a n h ( W c [ h ( t − 1 ) , x t ] + b c ) c_t = tanh(W_c [h_{(t-1)}, x_t] + b_c) ct=tanh(Wc[h(t−1),xt]+bc)
决定写入什么新信息。 - Output Gate(输出门): o t = s i g m o i d ( W o [ h ( t − 1 ) , x t ] + b o ) o_t = sigmoid(W_o [h_{(t-1)}, x_t] + b_o) ot=sigmoid(Wo[h(t−1),xt]+bo)
决定对外输出多少记忆。
记忆状态与隐藏状态更新的公式如下:
c t = f t ∗ c ( t − 1 ) + i t ∗ c t c_t = f_t * c_{(t-1)} + i_t * ~c_t ct=ft∗c(t−1)+it∗ ct
h t = o t ∗ t a n h ( c t ) h_t = o_t * tanh(c_t) ht=ot∗tanh(ct)
LSTM 是通过门控机制,控制"记什么、忘什么、输出什么",从而解决 RNN 长期依赖问题的模型。
3.3 RBF
RBF的知识点在 Pt.6。
3.3.1 RBF函数的基本属性
RBF(Radial Basis Function)是一类只依赖于"输入到某个中心点的距离"的函数。
一般形式: p h i ( x ) = p h i ( ∣ ∣ x − c ∣ ∣ ) phi(x) = phi(|| x - c ||) phi(x)=phi(∣∣x−c∣∣)
其中:
- x:输入向量
- c:中心(center)
最常见的 RBF 函数是高斯函数。
p h i ( x ) = e x p ( − ∣ ∣ x − c ∣ ∣ 2 / ( 2 ∗ s i g m a 2 ) ) phi(x) = exp( - ||x - c||^2 / (2 * sigma^2) ) phi(x)=exp(−∣∣x−c∣∣2/(2∗sigma2))
这是 RBF 神经网络中最常用的形式。
RBF 的基本属性如下:
- 径向对称性(Radial symmetry)
phi(x) 只和距离有关,与方向无关。 - 局部响应(Locality)
离中心近 → 输出大
离中心远 → 输出迅速衰减 - 非线性
RBF 是非线性函数,因此模型可以拟合复杂的非线性映射。 - 平滑性(Smoothness)
RBF 通常连续且可微。 - 单峰性(Unimodal)
在中心点 c c c处取最大值,且只有这一个峰。
3.3.2 RBF网络的结构
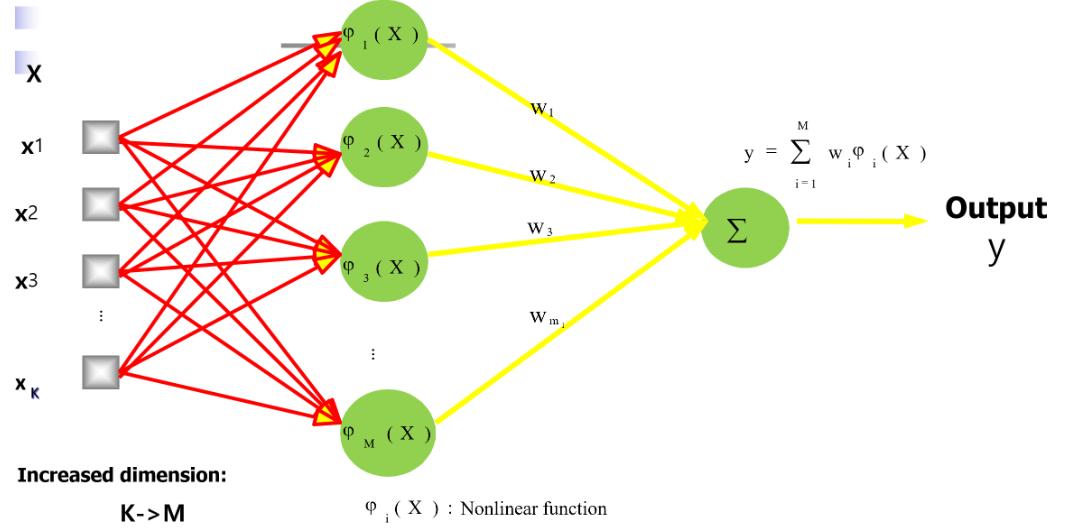
RBF 网络是一种三层前馈神经网络,包含输入层、RBF 隐层、 输出层。
- 输入层仅作信息传递,不进行任何非线性变换。
- 隐藏层由若干个 RBF 神经元组成,每个神经元对应一个中心 c i c_i ci
每个隐层神经元计算:
p h i i ( x ) = p h i ( ∣ ∣ x − c i ∣ ∣ ) phi_i(x) = phi(|| x - c_i ||) phii(x)=phi(∣∣x−ci∣∣)
最常见(高斯):
p h i i ( x ) = e x p ( − ∣ ∣ x − c i ∣ ∣ 2 / ( 2 ∗ s i g m a i 2 ) ) phi_i(x) = exp( - ||x - c_i||^2 / (2 * sigma_i^2) ) phii(x)=exp(−∣∣x−ci∣∣2/(2∗sigmai2)) - 输出层通常是线性组合,不使用激活函数,输出为:
y = s u m i ( w i ∗ p h i i ( x ) ) + b y = sum_i ( w_i * phi_i(x) ) + b y=sumi(wi∗phii(x))+b
3.3.3 RBF怎么确定中心
这门课教了两种方式:随机选择和k-均值聚类(K-means Clustering)。
3.4 有关 Pt.7 的问题
知识点:Pt.7。
3.4.1 时间序列的例子
例如:
- 股票价格(Stock prices):股票价格随时间变化,可以形成时间序列数据。
- 温度读数(Temperature readings):温度数据通常在固定的时间间隔(如每小时)记录,形成时间序列。
3.4.2 Elman 网络的结构
Elman 网络是一种 简单循环神经网络(Simple RNN)。
Elman网络包含以下几个部分:
- 输入层(Input):
输入层接收外部输入信号 x x x。 - 隐藏层(State/Hidden):
隐藏层处理输入信号,并生成内部状态 z z z。
隐藏层的输出不仅用于生成最终的输出,还被复制到上下文层(Context Layer)。 - 上下文层(Context Layer):
上下文层存储隐藏层的输出,作为网络的短期记忆。
上下文层的输出被反馈到隐藏层,形成循环连接。 - 输出层(Output):
输出层生成最终的输出 y y y,基于隐藏层的当前状态和上下文层的状态。
3.4.3 CEC 的定义
我认为这里还是考的是前面 LSTM 中的 CEC(恒定误差载体)。
它是一个特殊的单元状态 c t c_t ct,可以在时间步之间恒定地保留误差信息,使梯度不会因为长时间传播而消失(解决梯度消失问题)。
3.5 用神经网络分辨电池
现在有10个电池,其中有1个是赝品,赝品在重量/电压上有问题,现在我们需要想一个神经网络的方案去分辨电池。
3.5.1 方案
这道题较难,但是其实考的还是神经网络的知识点,我们需要说清楚输入和输出是什么。
参考答案如下:
由于赝品在重量和电压上存在异常,可将电池的重量和电压作为输入特征,利用神经网络学习正常电池的特征分布。通过比较各电池的重构误差或偏离程度,异常最大的电池判定为赝品。
3.5.2 如何在Matlab里实现(提出一个函数就行)
feedforwardnet(简单神经网络)或者trainAutoencoder(训练自编码器)都可以。