Python数据结构（十）：冒泡排序详解

本文是Python数据结构系列的第十篇，我们将深入探讨基本排序算法中的冒泡排序。排序是计算机科学中的基础问题，理解排序算法对于培养算法思维、优化程序性能至关重要。冒泡排序作为最直观的排序算法之一，是学习排序算法的良好起点。

一、排序算法概述

在计算机科学中，排序算法是一种将一串数据依照特定顺序进行排列的算法。排序算法的应用非常广泛，从简单的数据整理到复杂的数据库查询优化，都离不开排序操作。

排序的重要性：

数据组织：使数据更易于理解和分析
提高查找效率：许多查找算法（如二分查找）要求数据有序
数据分析基础：统计、聚合等操作通常需要排序后的数据
算法基础：排序是许多高级算法的基础组件

排序算法的分类：

基本排序算法：时间复杂度通常为O(n²)
- 冒泡排序（Bubble Sort）
- 选择排序（Selection Sort）
- 插入排序（Insertion Sort）
高级排序算法：时间复杂度通常为O(n log n)
- 快速排序（Quick Sort）
- 归并排序（Merge Sort）
- 堆排序（Heap Sort）

二、冒泡排序的基本概念

冒泡排序（Bubble Sort）是一种简单直观的排序算法。它重复地遍历要排序的数列，一次比较两个相邻元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。

2.1 冒泡排序的名称由来

这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端（升序排列时），就像水中的气泡一样逐渐上浮到水面，因此得名"冒泡排序"。

2.2 冒泡排序的基本思想

冒泡排序的基本思想是通过相邻元素之间的比较和交换，使较大的元素逐渐从前往后移动（升序排列时），就像气泡一样逐渐上浮。

冒泡排序的直观理解：

想象一下水中的气泡，越大的气泡上浮得越快。在排序过程中，较大的元素就像大气泡一样，通过一次次的比较和交换，逐渐"浮"到数组的末尾。

三、冒泡排序的算法原理

3.1 算法步骤

冒泡排序的算法步骤可以详细描述如下：

比较相邻元素：从数组的第一个元素开始，比较相邻的两个元素
交换位置：如果第一个元素比第二个大（升序排序），就交换它们的位置
遍历数组：对每一对相邻元素重复步骤1-2，从开始第一对到结尾最后一对
重复过程：针对所有元素重复以上步骤，除了最后一个已经排序好的元素
持续进行：重复整个过程，直到没有任何一对数字需要比较

3.2 排序过程演示

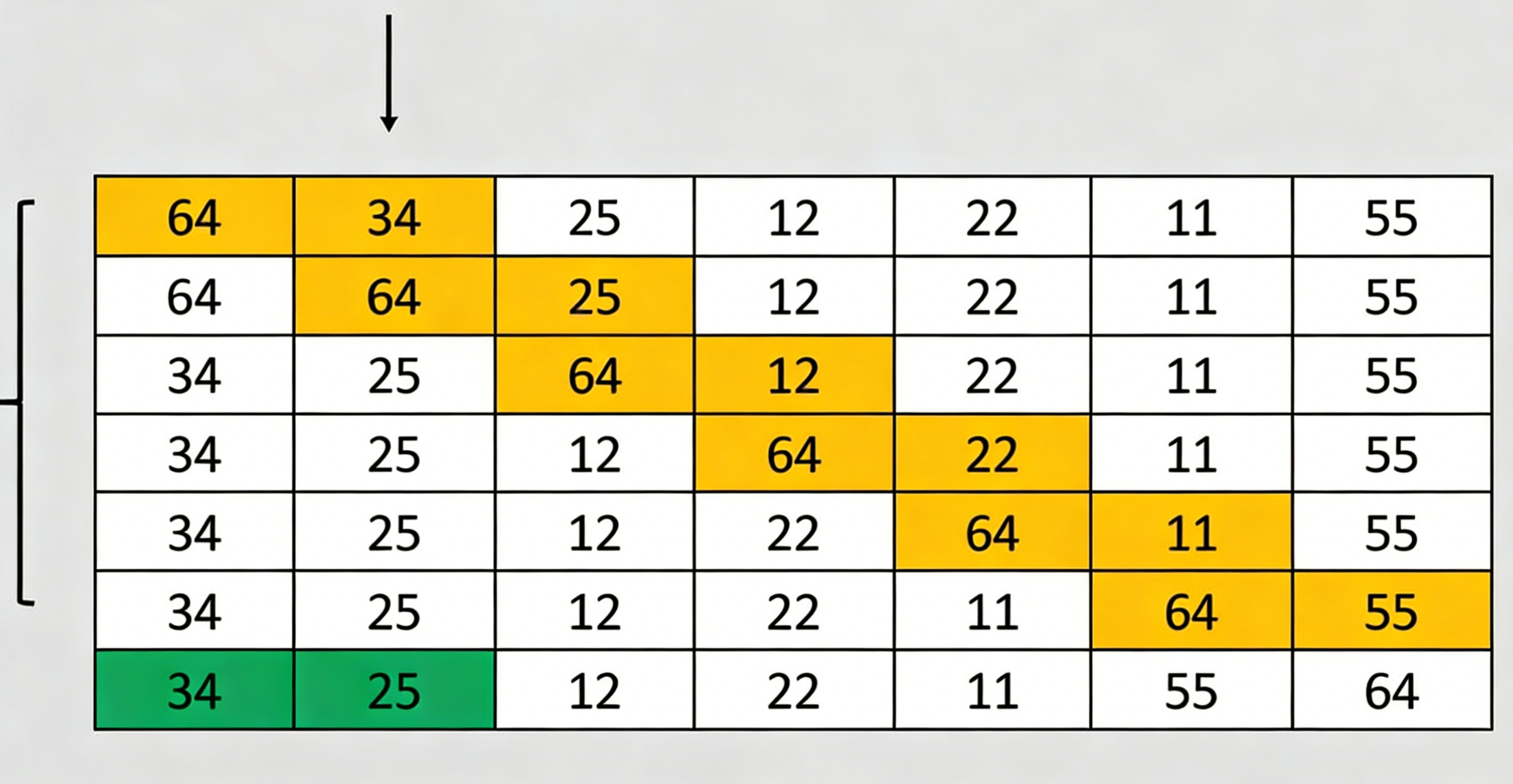
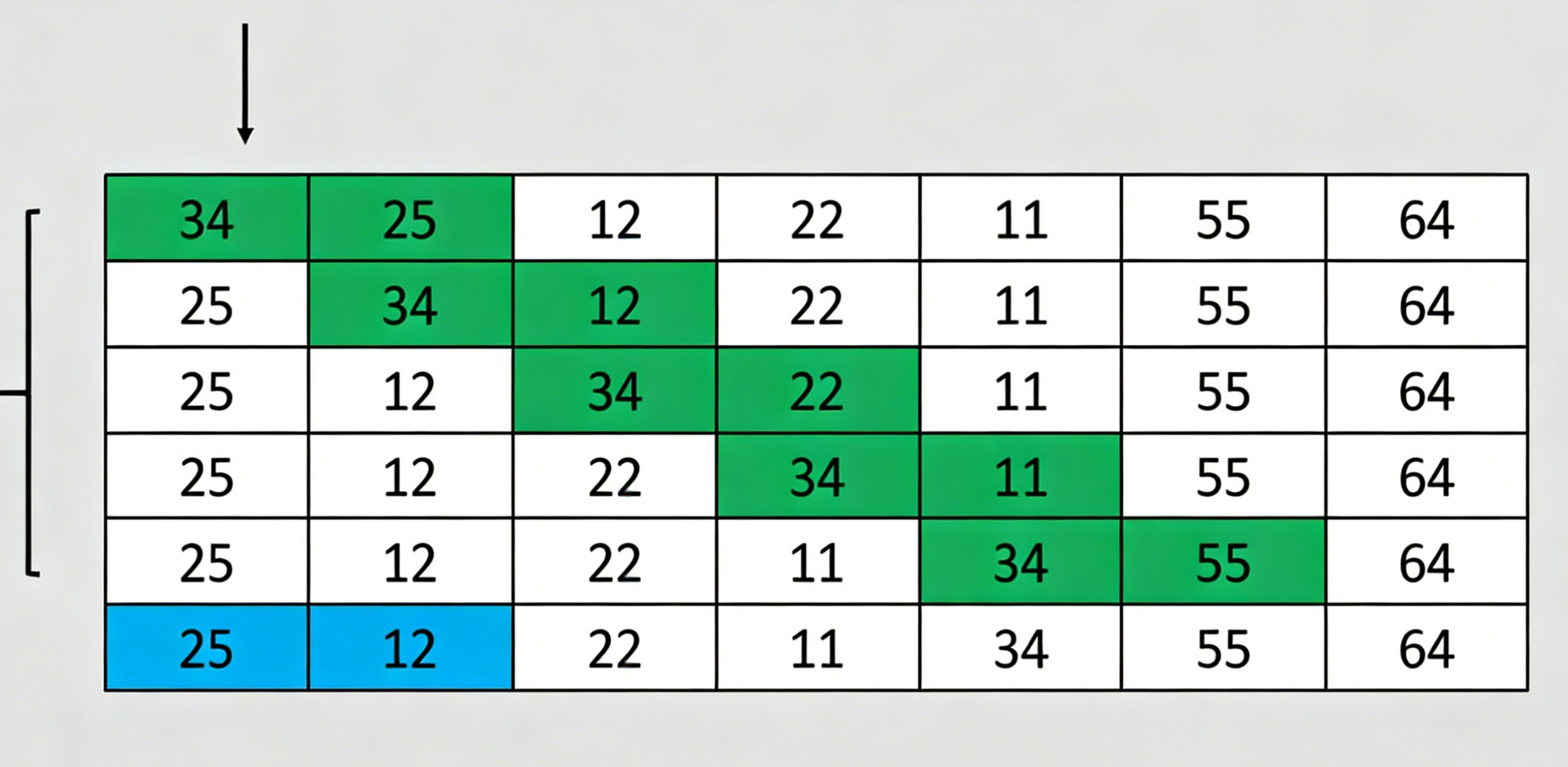
以下是一个具体的排序过程示例：

初始数组： [64, 34, 25, 12, 22, 11, 55]

第一轮排序：

比较64和34：64>34，交换 → [34, 64, 25, 12, 22, 11, 55]
比较64和25：64>25，交换 → [34, 25, 64, 12, 22, 11, 55]
比较64和12：64>12，交换 → [34, 25, 12, 64, 22, 11, 55]
比较64和22：64>22，交换 → [34, 25, 12, 22, 64, 11, 55]
比较64和11：64>11，交换 → [34, 25, 12, 22, 11, 64, 55]
比较64和55：64>55，交换 → [34, 25, 12, 22, 11, 55, 64]

第一轮结果： [34, 25, 12, 22, 11, 55, 64]（最大的元素64已就位）

第二轮排序：

比较34和25：34>25，交换 → [25, 34, 12, 22, 11, 55, 64]
比较34和12：34>12，交换 → [25, 12, 34, 22, 11, 55, 64]
比较34和22：34>22，交换 → [25, 12, 22, 34, 11, 55, 64]
比较34和11：34>11，交换 → [25, 12, 22, 11, 34, 55, 64]
比较34和55：34<55，不交换 → [25, 12, 22, 11, 34, 55, 64]

第二轮结果： [25, 12, 22, 11, 34, 55, 64]（第二大的元素55已就位）

继续这个过程直到数组完全排序...

四、Python实现冒泡排序

4.1 基础实现

python 复制代码

def bubble_sort(arr):
    """
    冒泡排序基础实现
    :param arr: 待排序的列表
    :return: 排序后的列表
    """
    # 获取数组长度
    n = len(arr)
    
    # 外层循环控制排序轮数
    for i in range(n - 1):
        # 内层循环进行相邻元素比较和交换
        for j in range(0, n - i - 1):
            # 如果前一个元素大于后一个元素，则交换它们
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    
    return arr

# 测试冒泡排序
arr = [64, 34, 25, 12, 22, 11, 55]
sorted_arr = bubble_sort(arr.copy())  # 使用副本，不修改原数组
print(f'原始数组: {arr}')
print(f'冒泡排序后: {sorted_arr}')

4.2 实现细节

外层循环 (i循环)

python 复制代码

for i in range(n - 1):

控制排序的轮数
对于长度为n的数组，需要进行n-1轮排序
每轮排序将一个元素放到正确的位置

内层循环 (j循环)

python 复制代码

for j in range(0, n - i - 1):

进行相邻元素的比较和交换
n - i - 1 表示每轮需要比较的元素对数
随着排序进行，已排序的部分不再参与比较

元素比较和交换

python 复制代码

if arr[j] > arr[j + 1]:
    arr[j], arr[j + 1] = arr[j + 1], arr[j]

比较相邻的两个元素
如果顺序错误则交换位置
Python的元组赋值使得交换操作简洁高效

4.3 排序过程可视化

为了更好理解冒泡排序的过程，我们可以添加打印语句来显示每一轮的排序结果：

python 复制代码

def bubble_sort_verbose(arr):
    """
    带详细输出的冒泡排序
    """
    n = len(arr)
    print(f"初始数组: {arr}")
    print(f"数组长度: {n}")
    print("-" * 40)
    
    for i in range(n - 1):
        print(f"第 {i + 1} 轮排序:")
        print(f"  需要比较 {n - i - 1} 对元素")
        
        for j in range(0, n - i - 1):
            print(f"    比较 arr[{j}]={arr[j]} 和 arr[{j+1}]={arr[j+1]}", end="")
            
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                print(f" → 交换 → {arr}")
            else:
                print(f" → 不交换")
        
        print(f"  第 {i + 1} 轮结果: {arr}")
        print("-" * 40)
    
    print(f"最终排序结果: {arr}")
    return arr

# 测试
arr = [64, 34, 25, 12, 22]
bubble_sort_verbose(arr.copy())

五、冒泡排序的时间复杂度分析

5.1 时间复杂度计算

最好情况（数组已排序）

需要n-1次比较
0次交换
时间复杂度：O(n)

最坏情况（数组完全逆序）

比较次数：第1轮n-1次，第2轮n-2次，...，第n-1轮1次
总比较次数：(n-1) + (n-2) + ... + 1 = n(n-1)/2
交换次数与比较次数相同
时间复杂度：O(n²)

平均情况

比较次数：大约n(n-1)/4次
交换次数：大约n(n-1)/4次
时间复杂度：O(n²)

5.2 空间复杂度

冒泡排序是原地排序算法
只需要常数级别的额外空间（用于临时交换）
空间复杂度：O(1)

5.3 时间复杂度总结

情况	比较次数	交换次数	时间复杂度	空间复杂度
最好	n-1	0	O(n)	O(1)
最坏	n(n-1)/2	n(n-1)/2	O(n²)	O(1)
平均	≈n(n-1)/4	≈n(n-1)/4	O(n²)	O(1)

六、冒泡排序的特点

6.1 优点

简单易懂：算法思想直观，容易理解和实现
原地排序：只需要常数级别的额外内存空间
稳定排序：相等元素的相对位置不会改变
适应性：对于已经部分排序的数组，性能较好

6.2 缺点

效率低下：时间复杂度为O(n²)，不适合大规模数据
交换频繁：即使元素已经有序，也可能进行不必要的比较
不实用：在实际应用中很少使用，主要作为教学示例

6.3 适用场景

教学目的：作为排序算法的入门教学
小规模数据：数据量很小（n < 100）时可以使用
几乎有序的数据：当数据已经基本有序时，性能尚可
稳定性要求高：需要稳定排序且数据量不大时

七、冒泡排序与其他排序算法的比较

7.1 与选择排序比较

特性	冒泡排序	选择排序
比较次数	O(n²)	O(n²)
交换次数	O(n²)	O(n)
稳定性	稳定	不稳定
适应性	对部分有序数据有适应性	无适应性
实现难度	简单	简单

7.2 与插入排序比较

特性	冒泡排序	插入排序
比较次数	O(n²)	O(n²)
交换次数	O(n²)	O(n²)
稳定性	稳定	稳定
适应性	对部分有序数据有适应性	对部分有序数据适应性更强
实际性能	通常比插入排序慢	通常比冒泡排序快

总结

冒泡排序是最基础、最直观的排序算法之一，虽然在实际应用中效率不高，但它在算法教学和编程基础训练中具有重要价值。

核心要点回顾：

基本思想：通过相邻元素的比较和交换，使较大元素逐渐"浮"到数组末端
算法复杂度：时间复杂度O(n²)，空间复杂度O(1)
稳定性：冒泡排序是稳定排序算法
实现简单：代码直观，易于理解和实现
教学价值：培养算法思维和编程基础的重要工具

学习建议：

理解原理：不仅要会写代码，更要理解算法的工作原理
手动模拟：在纸上手动模拟排序过程，加深理解
分析复杂度：学会计算和分析算法的时间复杂度和空间复杂度
比较学习：与其他排序算法比较，理解各自优缺点

在实际编程中，虽然很少直接使用冒泡排序，但理解它的原理对于学习更复杂的排序算法和培养算法思维都有重要意义。

在下一篇中，我们将探讨选择排序，这是另一种基本排序算法。选择排序通过每次选择最小（或最大）元素放到正确位置来实现排序，与冒泡排序有不同的特点和适用场景。

注意：本文是Python数据结构系列的第十篇，重点讲解冒泡排序的基本概念和实现。在实际编程中，对于排序需求，通常建议使用Python内置的排序函数或更高效的排序算法，但理解冒泡排序的原理对于培养算法基础和解决特定问题仍有重要价值。