可视化奇异值分解

在前面几篇文章中我们已经写下了一系列方程，这些方程从数学上定义了奇异值分解 (SVD) 的各个分量以及它们与输入矩阵 M 的关系。现在，让我们通过一些可视化，使这些导出的分量更加具象化。

图 1：方阵 M 的奇异值分解的 U 、 S 和 V 的可视化，其中 m=n

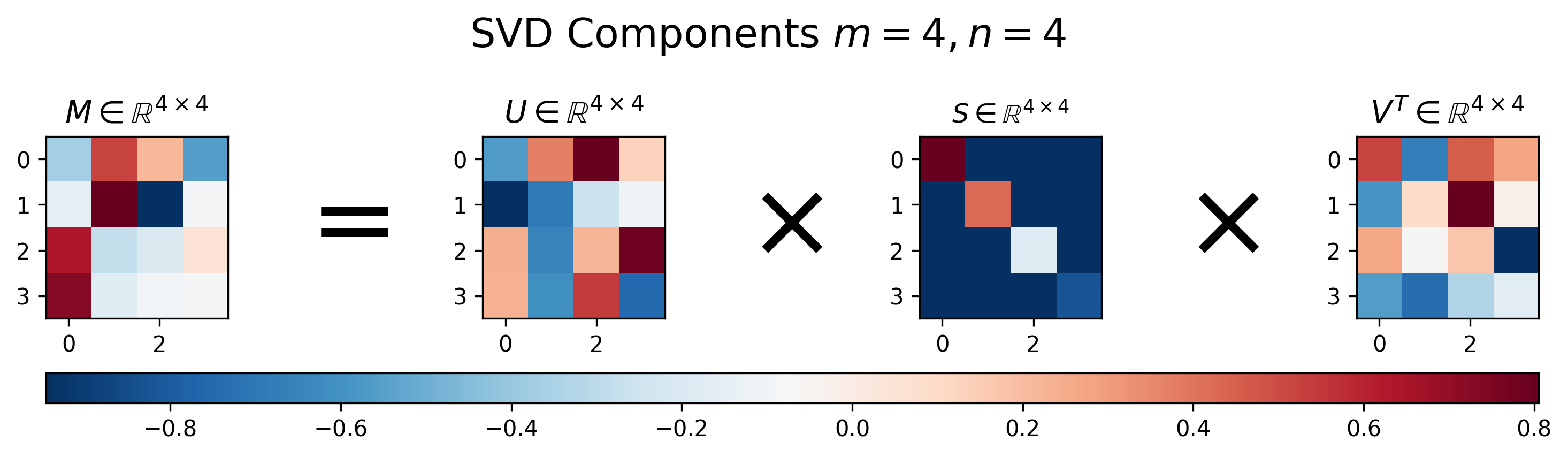
图 1：方阵 SVD 的"标准形态"（4×4 的例子）

这张图里有 4 个同样大小的热力图，从左到右可以理解为：

① 左一：原始矩阵 A

颜色红/蓝代表正负与大小，这就是你要分解的"混合变换"。

② 左二：U（左奇异向量矩阵）

U 的列向量是一组 正交单位基。

它的本质作用：

在输出空间里定义"最舒服的坐标轴"（一组正交方向）
你可以把它当成：把坐标系旋转到某个新方向

性质：

③ 左三：Σ（奇异值矩阵，只有对角线亮）

你会看到大部分格子都接近 0（深蓝），只有 对角线上有几个明显的亮块。

这就是 SVD 最"灵魂"的部分：

Σ 只做一件事：沿着某些轴做伸缩（拉伸/压缩）
对角线元素就是 奇异值

性质：

④ 右一：（右奇异向量的转置）

V 的列向量也是一组 正交单位基，但它属于"输入空间"。

它的作用：

在输入空间里先把向量换一套坐标系（旋转/镜像）
你可以理解为：把输入方向对齐到"最容易被拉伸的方向"

性质：

✅ 图 1 的一句话总结：

A(任意复杂)=U(输出旋转) Σ(轴向缩放) (输入旋转)

图 2：高矩阵 M 的奇异值分解的 U 、 S 和 V 的可视化，其中 m>n 。

图 2：矩形矩阵的 SVD（"不是方阵也能拆！"）

这张图的关键点是：中间那个 Σ 变成"长方形对角阵"。

你会看到一个高高的深蓝矩阵，里面斜对角有几块亮色方块------这就是：

比如 m>n（高矩阵）时：

Σ 最多只有 n 个奇异值
也就是说最多只有 min⁡(m,n) 个"有效拉伸方向"

所以矩形矩阵的 SVD 依然成立：

✅ 图 2 的一句话总结 ：
矩阵不必是方阵，SVD 仍然能把它拆成"旋转 + 拉伸 + 旋转"，只不过拉伸那一步的 Σ 是长方形。

图 3：宽矩阵 M 的奇异值分解的 U 、 S 和 V 的可视化，其中 m<n 。

图 3：SVD 的"秩"与"信息量"------为什么只亮了几格？

你会注意到：第三张图里有一个 Σ（或类似形态）只亮了很少几个对角块，这在暗示一个超重要事实：

很多矩阵虽然看起来很乱，但真正"有用的结构"只集中在前几个奇异值上。

SVD 有一个等价表达式特别关键：

这句话很炸裂，它说：

每一项都是一个 秩 1 矩阵
是"一个方向 × 另一个方向"的外积
决定这一项的"贡献强弱"

所以你在热力图里看到的效果就是：

第一项（σ1）贡献最大
后面的项越来越小
小到可以忽略，就像图里"几乎没颜色"

✅ 图 3 的一句话总结：

A 可以看成很多个"秩 1 图案"的叠加，而真正重要的往往只有前几个。

图 4，奇异向量构成正交基

左列显示了对随机矩阵 [m×n]=[10×5] 进行奇异值分解 (SVD) 后得到的 U 和矩阵。中间列绘制了沿每个矩阵的奇异向量（列）计算的 L2 范数；所有奇异向量的范数均为 1。右列显示了每个矩阵与其自身的内积；该内积为单位矩阵，表明奇异向量的正交性。

L2 范数（读作 "L-two 范数"）最直观的理解就是：

一个向量的"长度"（欧几里得距离）

也叫 欧几里得范数 / Euclidean norm。

1）向量的 L2 范数定义

对向量

它的 L2 范数是：

例子（2 维）

这就是熟悉的 3-4-5 直角三角形。

2）为什么叫 "L2"？

因为它来自一个更通用的范数家族：

当 p=2 时，就是 L2。

3）几何意义（非常重要）

在 2D 平面中：

表示所有距离原点为 r 的点

→ 形成一个圆
在 3D 中

→ 形成一个球面

所以 L2 范数对应我们最熟悉的"圆形/球形距离"。

4）矩阵也有 L2 范数吗？

有，而且在机器学习里也常见：

（1）向量的 L2：长度

（2）矩阵的 "L2 范数"（谱范数 / 2-范数）

矩阵 A 的 2-范数定义是：

意思是：

把所有单位向量 x 都试一遍，

看 Ax 被拉伸得最长能到多少。

这就是矩阵对空间的"最大放大倍数"。

并且它恰好等于 最大奇异值：

5）机器学习里为什么爱用 L2？

因为它有两个"好用"特点：

光滑可导（适合梯度下降）
惩罚大数更狠（平方会放大大参数）

常见的 L2 正则化（Ridge / Weight Decay）就是：

✅一句话记住：

向量的 L2 范数 = 长度
矩阵的 L2 范数 = 最大拉伸倍数 = 最大奇异值

这张图到底在展示什么？

先读标题你就能发现关键点：

左上写着：
左下写着：

也就是说：

✅ 图 4 展示的是 U 和，并验证它们"是否真的是正交矩阵"。

属性 1：热力图本身 ------ "我确实拿到了 U 和 "

左上：U 的热力图

它就是一个 10×10 矩阵，每个格子是一项。

左下：的热力图

是一个 5×5 矩阵，每个格子是一项。

这一块只是告诉你：SVD 给出的 U、长什么样（数值分布如何）。

属性 2：中间的柱状图 ------ "每一列都是单位向量（L2 范数 = 1）"

上中：L2 Norm of U Columns

意思是：对 U 的每一列，计算

你看到每根柱子都≈1，说明：

✅ U 的每一列都是单位向量

（长度都是 1）

下中：L2 Norm of Columns

注意这里检查的是的列。

而的列，其实就是 V 的行。

但无论检查列还是行，只要是正交矩阵，都应当满足：

每列长度为 1
每行长度也为 1

所以这组柱子全≈1，说明：

✅ V（以及）也是单位正交基

属性 3：右边的热力图 ------ "互相垂直（正交） ⇒ 乘出来是单位矩阵 I"

这是最硬核的验证。

右上：

如果 U 真是正交矩阵，那么必须满足：

你看到右上那张图：

对角线全是亮黄（≈1）
其他地方几乎全深蓝（≈0）

这正是单位矩阵的样子。

✅ 所以它证明：
U 的列不仅长度为 1，而且两两垂直。

右下：

同理，如果 V 正交，就有：

你右下看到的也是：

对角线≈1
其他≈0

✅ 所以它证明：
V 也是正交矩阵。

一句话总结：这张图在验证 SVD 的哪三个"属性"？

这张图展示/验证的是：

结构属性 ：SVD 得到了、（左侧热力图）
单位长度属性：U、V 的每个基向量都是单位向量（中间柱状图全部≈1）
正交属性：

（右侧单位矩阵"黄对角线 + 蓝背景"）

从这张图推测原矩阵 A

根据图中的维度：

是
是
那么原矩阵必然是一个的矩阵（10 行 5 列）。
中间缺失的矩阵将是一个的对角矩阵，对角线上是从大到小排列的奇异值。

总结

这张图是 SVD 性质的完美验尸报告：

它直观地验证了 SVD 的数学定义：任何矩阵 A 都可以被分解为两个正交矩阵 () 和一个对角矩阵 () 的乘积。

图中的纯黄色对角线和纯深蓝色背景，就是数学中美妙的 "正交性" 的视觉体现。

图 5 以可视化的方式展示了图 4 中计算/展示的 SVD 结果的三个属性。

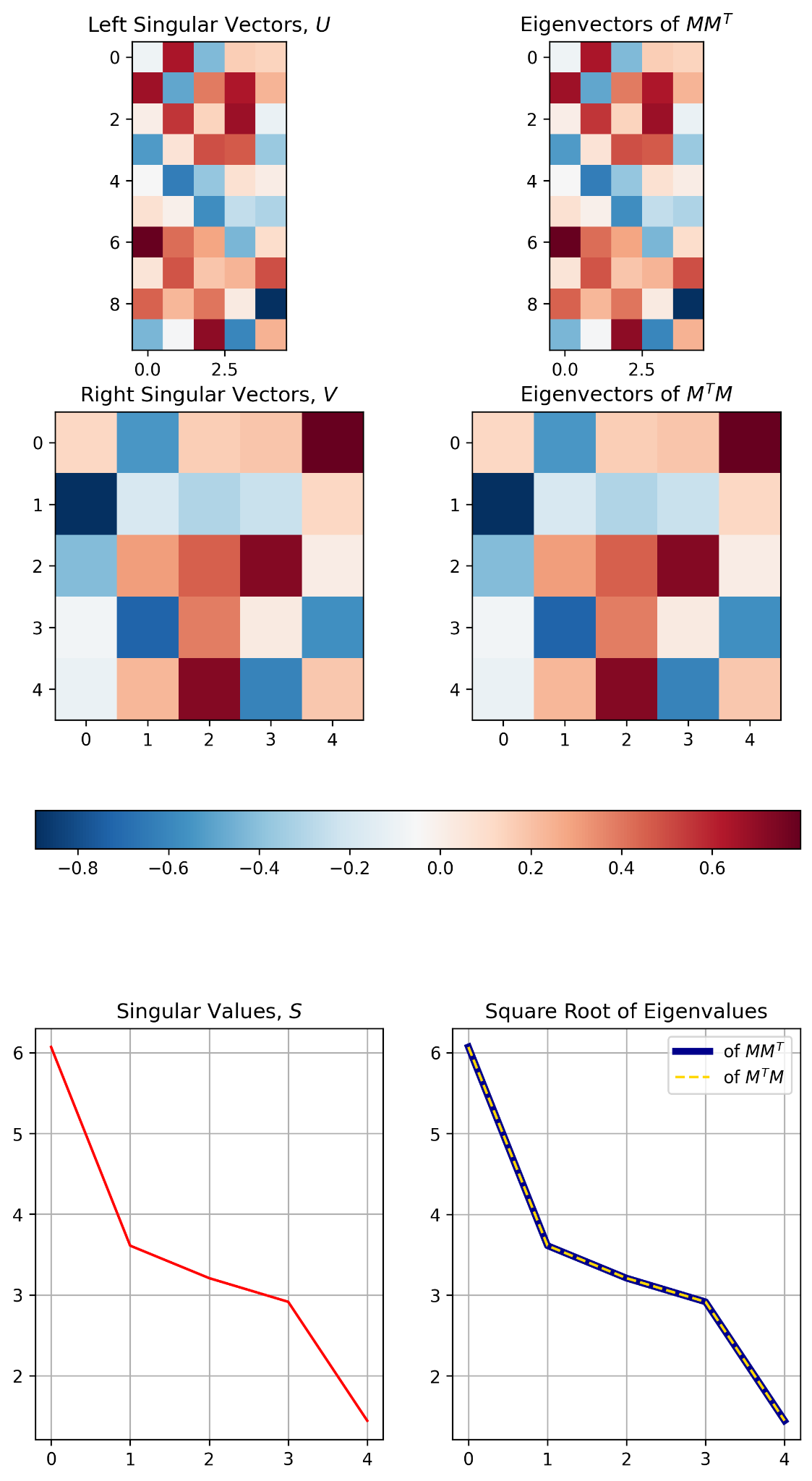
这张图其实是在用可视化 把图 4 的 SVD 结果的 3 个关键属性"钉死在眼睛里"。我按从上到下、从左到右，把它归纳成 3 点：

①（最上面两张长条热力图）SVD 可以把原矩阵"完全重构"

你看到左上、右上两张 几乎一模一样的长方形热力图：

左上：原始矩阵 M
右上：用 SVD 分解再乘回去得到的重构矩阵

它们一致，说明一个事实：

✅ SVD 不是近似方法，它首先是一个"精确分解"

只要保留全部奇异值（完整 Σ），就能 100%还原原矩阵。

②（中间两张方阵热力图）与的"非零谱"相同

中间那两张方阵热力图也是 几乎一模一样：

左中：（输出空间的 Gram/协方差型矩阵）
右中：（输入空间的 Gram/协方差型矩阵）

它们"谱意义上的等价"是 SVD 的核心桥梁：

✅ 所以结论是：

两者的 非零特征值完全相同
并且都等于

这就是为什么：

U 来自的特征向量
V 来自的特征向量
Σ 统一管理它们的"强度"（奇异值）

③（最下面两张折线图）奇异值衰减曲线 + "平方关系"被验证

底部两张图分别在讲两个重点：

左下红色折线：奇异值谱（Singular Value Spectrum）

红线明显从大到小下降，说明：

σ1 最大，代表"最主要结构"
越往后越小，代表"次要结构 / 细节 / 噪声"

✅ 这就是低秩近似为什么成立：

只用前 k 个奇异值就能抓住大部分信息：

右下蓝线 vs 黄虚线：两边特征值几乎重合

图例写着：

蓝色：eigs of
黄色虚线：eigs of

两条线几乎重合，视觉上证明了第②点：

✅ 它们的非零特征值相同

而结合 SVD 的关系就是：

一句话总归纳（这图展示的 SVD 三大属性）

可重构性 ：完整 SVD 能精确还原矩阵
双 Gram 同谱 ：与共享同一组非零特征值（= ）
能量集中：奇异值快速衰减 → 信息主要集中在前几个 → 低秩近似/压缩/降噪成立

把 SVD 原理"讲透"的一条主线

你可以把 SVD 牢牢记成下面这 5 句话（完全够你吃透它）：

1）SVD 是在描述一个线性变换如何扭曲空间

把单位圆（或单位球）经过 A 变换，会变成一个椭圆（或椭球）。

椭球的主轴方向：由 U 给出（输出空间）
椭球主轴长度 ：由给出
输入空间对齐主轴的方向：由 V 给出

2）V 给"输入最敏感的方向"，U 给"输出对应的方向"

这句是 SVD 的核心物理意义：

往方向输入一个单位向量
输出一定落在方向
长度被放大/缩小倍

3）奇异值来自特征值：SVD 其实是"把特征分解做到了任意矩阵"

所以：

是的特征向量
是的特征向量
是对应特征值

4）SVD = 旋转 + 拉伸 + 再旋转

对任意向量 x：

按步骤读就是：

：把输入坐标系旋转到"主方向坐标系"
：沿各轴拉伸/压缩
：再旋转到输出空间

5）截断 SVD 是"最优低秩近似"，也是 PCA、压缩、去噪的底层

这就是：

图片压缩（只保留主要纹理）
推荐系统矩阵补全
NLP 里的语义空间压缩
PCA 的矩阵版本

图 1～图 3 下面那条带刻度的长条 ，叫做 颜色条 / 色标（colorbar），它的作用是：

把"颜色"翻译成"数值大小"

让你知道热力图里每个格子的颜色到底对应多大、是正还是负。

1）它表示什么数？

热力图里的每一个小格子，对应矩阵里的一个元素 aija_{ij}aij。

颜色条告诉你：

蓝色 → 数值是负数（越蓝越小、越负）
白色 → 数值接近 0
红色 → 数值是正数（越红越大、越正）

所以它本质上就是：

(数值)

2）为什么中间通常是白色？

因为很多绘图默认用的是"发散色图"（diverging colormap），把 0 放在中间：

负数往一边渐变成蓝
正数往另一边渐变成红

这样你能一眼看出"符号"和"强弱"。

3）刻度代表什么？

刻度就是具体数值范围，比如可能会标：