LeetCode:路径总和 III

文章目录

[1. 题目简介](#1. 题目简介)
[2. 题目解析](#2. 题目解析)
- [2.1 暴力枚举 dfs](#2.1 暴力枚举 dfs)
- [2.2 前缀和优化](#2.2 前缀和优化)

1. 题目简介

2. 题目解析

2.1 暴力枚举 dfs

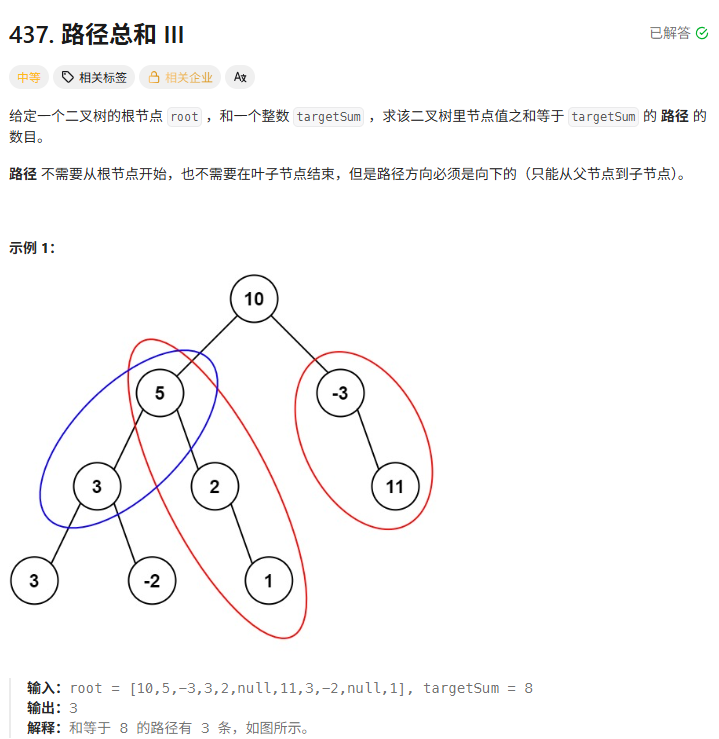
这道题目需要统计所有等于targetNum的路径总数，题中的路径要求是灵活的，不需要从根结点开始，无需在叶子结点结束，方向则是要求严格向下，从父结点到子结点。

刚开始拿到此题时，很容易想到一种暴力做法：走先序遍历逻辑，这样天然支持从根结点开始向下遍历所有结点，再使用一个变量动态记录路径和，每个结点选或不选，两种情况。 这种做法是不行的，因为会出现互相间隔的两个结点同时选中，而中间结点不选，这样的路径是非法的。

上述方法，如果每个结点都选，那么此时路径便是严格从根结点开始，不满足题目路径要求，实质这样会少统计，因为统计了所有严格从根结点开始的路径，却没有统计从其它结点开始的路径。

因此，在上述分析下，我们自然想到一种做法：从某个结点开始的所有路径可以通过遍历，轻松枚举，那么只需要对整棵树中的每个结点都暴力统计所有路径，那么自然就穷尽了所有符合题目要求的路径。

上述对于一个结点开始路径的dfs枚举，使用前序遍历，因为前序遍历顺序为根左右 ，这样到达的根结点最快结算 ，路径的延伸和枚举，也更直观，更符合直觉。

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int dfs(TreeNode* root, long long targetSum) {
        if(!root)
            return 0;
        int ret = 0;
        targetSum -= root->val;
        if(targetSum == 0)
            ret++;
        ret += dfs(root->left, targetSum);
        ret += dfs(root->right, targetSum);
        return ret;
    }
    int pathSum(TreeNode* root, int targetSum) {
        if(!root)
            return 0;
        int ret = dfs(root, targetSum);
        ret += pathSum(root->left, targetSum);
        ret += pathSum(root->right, targetSum);
        return ret;
    }
};

上述算法时间复杂度在 O(n ^ 2)，空间复杂度在 O(n)，因为每个结点都需要暴力枚举所有路径，而每个结点枚举中，最坏可能穷尽结点数接近 n 个结点(非平衡二叉树，二叉树退化为链表情况)，最坏空间复杂度同样在二叉树退化为链表时达到。

2.2 前缀和优化

在上述暴力枚举每个结点过程中，存在大量重复计算，因为父结点中路径和的一部分，本质就是其子结点或孙子结点的路径和，而这些路径和在暴力枚举中，被大量重复计算了，那么能否优化这些重复计算呢？

虽然此题是树形结构 ，但是仔细审题，发现路径严格要求自上而下，严格从父结点到子结点，同时路径的起始位置无严格要求 ，这道题就与"和为K的子数组"，本质相同，都可以通过哈希 + 前缀和方式，将 N^2 的复杂度优化到 N。

那么，根据上述思路，我们得到 dfs 本质要做什么：统计整颗二叉树中，以其中每个结点作为结束结点合法路径总数，并将合法路径树返回。而在递归中，仅需处理当前情况：维护到当前结点的前缀和，根据哈希获得以当前结点为结尾的合法路径数，维护前缀和哈希结构，然后再分别递归左右子树即可。

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<long long,int> prefix;
    int dfs(TreeNode* root, long long sum, int targetSum) {
        if(root == nullptr)
            return 0;
        sum += root->val;
        int ret = prefix[sum - targetSum];
        
        prefix[sum]++; // 维护前缀和哈希结构
        ret += dfs(root->left, sum, targetSum);
        ret += dfs(root->right, sum, targetSum);
        prefix[sum]--; // 需要理解这一步回溯,关键所在
        
        return ret;
    }
    int pathSum(TreeNode* root, int targetSum) {
        prefix.clear();
        prefix[0] = 1; // 关键的初始化
        return dfs(root, 0, targetSum);
    }
};