leetcode 2976(Floyd-Warshall 算法)

2976: 转换字符串的最小成本Ⅰ

思路：将字符转换 问题建模为图的最短路径 问题，使用 Floyd-Warshall 算法预处理所有字母对之间的最小转换成本。

1. 问题建模

• 将 26 个小写字母看作图中的 26 个节点
• 每个转换规则 original[i] -> changed[i] 看作一条有向边，权重为 cost[i]
• 目标：找到从source中每个字符到target中对应字符的++最小++转换成本

2. 初始化距离矩阵

• 创建一个 26×26 的二维数组 g，存储所有字母对之间的最小转换成本
• 对角线元素初始化为 0 （同一字符转换成本为 0）
• 其他元素初始化为一个很大的数 INF （这里用 0x3f3f3f3f）

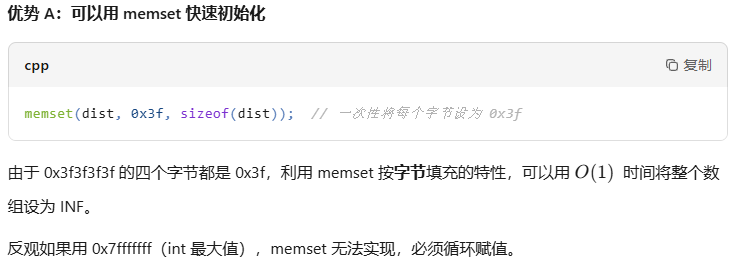
为什么选择 0x3f3f3f3f？

0x3f3f3f3f（十进制约1,061,109,999，即 10^9 级别）是算法竞赛中常用的"无穷大"值。

3. 添加直接转换边

• 遍历所有给定的转换规则
• 对于每条规则 original[i] -> changed[i]，取权重的最小值 （因为可能有重复规则）

4. Floyd-Warshall 算法

• 三重循环：k → i → j
• 对于每个中间节点 k，尝试通过 k 来缩短 i 到 j 的路径
• 核心公式：g[i][j] = min(g[i][j], g[i][k] + g[k][j])
• 算法结束后，g[a][b] 就是从字母 a 转换到字母 b 的最小成本

5. 计算总成本

• 遍历 source 和 target 的每个位置

• 如果当前字符相同，跳过 （成本为 0）

• 如果 g[source_char][target_char] == INF，说明无法转换，返回 -1

• 否则累加最小转换成本

  class Solution {
  public:
  long long minimumCost(string source, string target, vector<char>& original, vector<char>& changed, vector<int>& cost) {
  int g[26][26];
  memset(g,0x3f,sizeof(g));
  for(int i=0;i<26;i++) g[i][i]=0;
  for(int i=0;i<original.size();i++){
  int x=original[i]-'a',y=changed[i]-'a';
  g[x][y]=min(g[x][y],cost[i]);
  }
  for(int k=0;k<26;k++){
  for(int i=0;i<26;i++){
  if(g[i][k]>=0x3f3f3f3f) continue;
  for(int j=0;j<26;j++){
  g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
  }
  }
  }
  long long ans=0;
  for(int i=0;i<source.size();i++){
  int a=source[i]-'a',b=target[i]-'a';
  if(g[a][b]>=0x3f3f3f3f) return -1;
  ans+=g[a][b];
  }

        return ans;
    }

  };