【算法】LeetCode『二分查找』

🎬 个人主页 ：MSTcheng · CSDN
🌱 代码仓库 ：MSTcheng · Gitee
🔥 精选专栏 : 《C语言》
《数据结构》
《算法学习》
《C++由浅入深》

💬座右铭：路虽远行则将至，事虽难做则必成！

前言：前面的文章中我们向大家介绍了滑动窗口算法，本篇文章就来介绍一下二分查找算法。

一、二分查找算法介绍

二分查找是一种在有序数组中快速定位目标值的算法。通过每次将搜索范围减半，其时间复杂度为 O(log n)，效率远高于线性查找。

算法步骤：

初始化左右指针 left 和 right，分别指向数组起始和末尾。

计算中间索引 mid = left + (right - left) （避免整数溢出）。比较 arr[mid] 与目标值：

若 arr[mid] == target，返回 mid。
若 arr[mid] < target，调整 left = mid + 1，继续搜索右半部分。
若 arr[mid] > target，调整 right = mid - 1，继续搜索左半部分。
重复上述过程直至 left > right，若未找到则返回 -1。

由于二分算法的思路比较简单，这里直接给出具体的步骤，本篇文章讲的是最基础的二分算法，进阶的二分算法将会在后面介绍！

了解完了二分算法，下面来看题目：

二、二分查找

2.1题目展示

2.1题目示例

示例 1:

复制代码

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

复制代码

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

2.3题目解析

本题的题意非常简单，这里就不过多赘述。

2.4算法原理

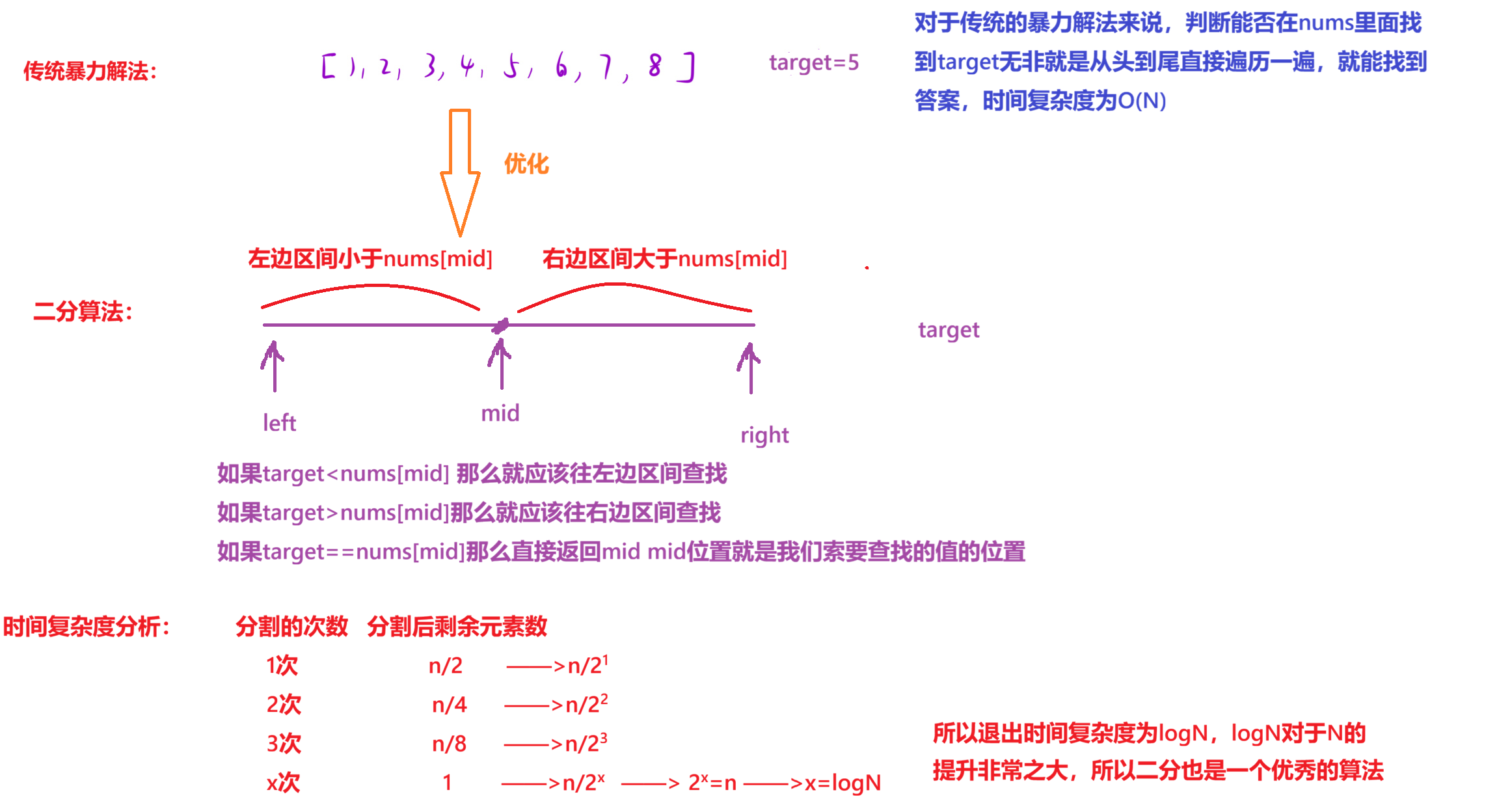
2.5代码编写

cpp 复制代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
        //定义两个指针
        int left=0,right=nums.size()-1;
        int mid=0; 
        while(left<=right)
        {
            
            if(left!=0&&right!=0)
                mid=(left+right)/2;

            if(nums[mid]<target)
            {
                //小于往右边查找
                left=mid+1;
            }    
            else if(nums[mid]>target)
            {
                //大于往左边查找
                right=mid-1;
            }
            else//(nums[mid]==target)
            {
                return mid;
            }
        }

        return -1;

    }
};

三、总结

二分查找的朴素模板：

cpp 复制代码

while (left<= right)
{
	int mid =left + (right-left) /2;
	if(......)
		left =mid+1;
	else if(......)
		right = mid-1;
	else
	return......
}

二分查找的适用条件：

复制代码

数据必须为有序数组（升序或降序）。
仅适用于可通过索引随机访问的数据结构（如数组，不适用于链表）。