《算法竞赛从入门到国奖》算法基础:搜索-多源BFS

💡Yupureki:个人主页

✨个人专栏:《C++》《算法》

🌸Yupureki🌸的简介:

[1. 矩阵距离](#1. 矩阵距离)

[2. 刺杀大使](#2. 刺杀大使)

前言

当问题中只存在一个起点时，这时的最短路问题就是单源最短路问题。而当问题中存在多个起点而不是单一起点时，这时的最短路问题就是多源最短路问题。

多源最短路的解决方案就是把这些源点汇聚在一起 ，当成一个"超级源点"。然后从这个"超级源点"开始，处理最短路问题。

初始化的时候，把所有的源点都加入到队列里面；

然后正常执行bfs的逻辑即可。

也就是初始化的时候，比普通的bfs多加入几个起点。

1. 矩阵距离

题目链接:

矩阵距离

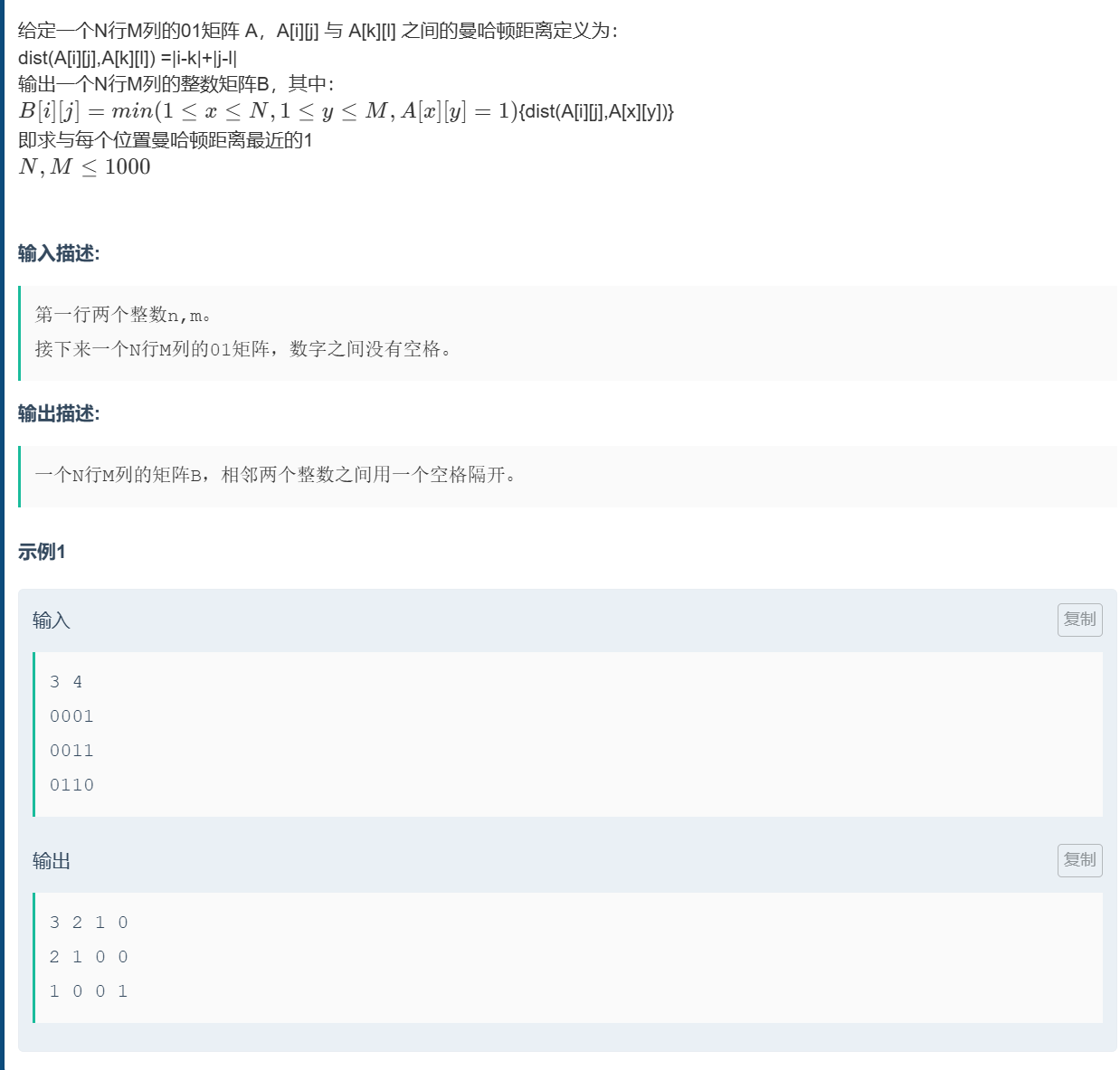
算法原理

正难则反：

如果针对某一个点，直接去找最近的1，我们需要对所有的0都来一次6fs，这个时间复杂度是接受不了的。
但是我们如果反着来想，从1开始向外扩展，每遍历到一个0就更新一下最短距离。这样仅需一次bfs，就可以把所有点距离1的最短距离更新出来。

正难则反是很重要的思想，后续还有很多题可以用到这个思想。

由于1的数量很多，我们在初始化阶段把所有1的坐标加入到队列中，然后正常bfs。

实操代码

cpp 复制代码

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int n, m;
vector<vector<int>> v;
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };

void bfs()
{
    vector<vector<int>> ret(n, vector<int>(m, 0));
    queue<pair<int, int>> q;
    v.resize(n);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            char num; cin >> num;
            v[i].push_back(num - '0');
            if (num == '1')//把所有的1都加入队列中
                q.push({ i,j });
        }
    }
    while (q.size())
    {
        auto p = q.front();
        q.pop();
        int a = p.first;
        int b = p.second;
        for (int k = 0; k < 4; k++)
        {
            int x = a + dx[k];
            int y = b + dy[k];
            if (x < 0 || x >= n || y < 0 || y >= m || v[x][y] == 1 || ret[x][y])
                continue;
            ret[x][y] = ret[a][b] + 1;
            q.push({ x,y });
        }
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cout << ret[i][j] << " ";
        }
        cout << endl;
    }
}

int main()
{
    cin >> n >> m;
    bfs();
    return 0;
}

2. 刺杀大使

题目链接:

P1902 刺杀大使 - 洛谷

算法原理

关键词:所有最大值中的最小值

这是很经典二分答案的题目说法，而我们也能发现对于所有的伤害值，一定存在一个界限x，使得

大于或等于x的伤害值一定能通过机关
小于x的伤害值一定不能通过机关

因此我们通过二分枚举答案，对于每一个二分结果，进行检查，是否能通过机关

具体如何判断通过，我们发现可以从第一行任意一个格子出发，因此我们把第一行所有的格子都加入节点，然后通过BFS判断

实操代码

cpp 复制代码

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int n, m;
vector<vector<int>> v;
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };

bool bfs(int ret)
{
    queue<pair<int, int>> q;
    vector<vector<bool>> mem(n, vector<bool>(m, false));
    for (int j = 0; j < m; j++)
    {
        q.push({ 0,j });//将第一行所有的格子都加入队列
    }
    while (q.size())
    {
        auto p = q.front();
        q.pop();
        int a = p.first;
        int b = p.second;
        if (a == n - 1)
            return true;
        for (int k = 0; k < 4; k++)
        {
            int x = a + dx[k];
            int y = b + dy[k];
            if (x < 0 || x >= n || y<0 || y >= m || mem[x][y] || v[x][y] > ret)
                continue;
            mem[x][y] = true;
            q.push({ x,y });
        }
    }
    return false;
}

int main()
{
    int left = 0;
    int right = 0;
    cin >> n >> m;
    v.resize(n);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            int num; cin >> num;
            v[i].push_back(num);
            if (num > right)
                right = num;
        }
    }
    while (left < right)//二分答案
    {
        int mid = (left + right) / 2;
        if (bfs(mid)) right = mid;
        else left = mid + 1;
    }
    cout << left;
    return 0;
}