【MCM】((N_G,N_A)) 可行域； ((C_R,c_E)) 分区图

import numpy as np
import matplotlib.pyplot as plt

# Given / assumed parameters for plotting
M = 1e8                 # tons
H = 3
Q_h = 179000            # tons/year per harbour
Q_E = H * Q_h           # total elevator nominal throughput (tons/year)
m = 125                 # tons/launch (representative within [100,150])
Tstars = [1, 2, 3]      # years
NA0 = Q_E / m           # boundary NA = Q_E/m

def plot_A(Tstar, outpath):
    req = M / (m * Tstar)  # required launches/year if only rockets (or total launches if in region I)
    
    # Prepare NA grid for boundary curve (piecewise)
    NA_vals = np.logspace(0, np.log10(req*2), 600)  # from 1 to 2*req
    boundary_NG = np.where(NA_vals < NA0, np.maximum(req - NA_vals, 1e-9), np.maximum(req - NA0, 1e-9))
    
    fig = plt.figure(figsize=(9, 6))
    ax = plt.gca()
    
    # Hybrid feasibility boundary
    ax.plot(NA_vals, boundary_NG, label=r'Hybrid boundary: $mN_G+\min(Q_E,mN_A)=M/T^*$')
    
    # Split NA = Q_E/m
    ax.axvline(NA0, linestyle='--', label=r'Split: $N_A=Q_E/m$')
    
    # Rocket-only feasibility (independent of N_A)
    ax.axhline(req, linestyle=':', label=r'Rocket-only feasible: $N_G=M/(mT^*)$')
    
    # Apex rocket requirement line (independent of N_G)
    ax.axvline(req, linestyle=':', label=r'Apex-rocket req: $N_A=M/(mT^*)$')
    
    # Capacity check annotation
    D = M / Tstar
    cap_ok = D <= Q_E
    ax.text(0.02, 0.02,
            (r'Capacity check: $M/T^*\leq Q_E$ is ' + ('TRUE' if cap_ok else 'FALSE')
             + '\n' + rf'$Q_E={Q_E:,.0f}$ tons/yr,  $M/T^*={D:,.0f}$ tons/yr'),
            transform=ax.transAxes, fontsize=10, va='bottom')
    
    ax.set_xscale('log')
    ax.set_yscale('log')
    ax.set_xlabel(r'$N_A$ (apex $\to$ Moon launches / year)')
    ax.set_ylabel(r'$N_G$ (ground $\to$ Moon launches / year)')
    ax.set_title(rf'Figure A: Feasible region in $(N_G,N_A)$ for deadline $T^*={Tstar}$ years'
                 + f'\n(Using $m={m}$ tons/launch, $Q_E=3\\times179,000$ tons/yr)')
    
    ax.set_xlim(1, req*2)
    ax.set_ylim(1, req*2)
    ax.legend(fontsize=9, loc='upper right')
    ax.grid(True, which='both', linestyle='--', linewidth=0.5)
    
    plt.tight_layout()
    plt.savefig(outpath, dpi=200)
    plt.close(fig)

# Generate A plots for T*=1,2,3
paths_A = []
for T in Tstars:
    p = f"/mnt/data/figure_A_Tstar_{T}.png"
    plot_A(T, p)
    paths_A.append(p)

# Figure B: cost partition in (C_R, c_E)
lambda_discount = 0.5  # example; user can change
slope = (1 - lambda_discount) / m  # c_E = slope * C_R

CR_max = 1e10
CR_vals = np.linspace(0, CR_max, 400)
cE_line = slope * CR_vals

fig = plt.figure(figsize=(9, 6))
ax = plt.gca()
ax.plot(CR_vals, cE_line, label=rf'Break-even: $c_E=\frac{{1-\lambda}}{{m}}C_R$  (here $\lambda={lambda_discount}$, $m={m}$)')

# Region labels
ax.text(CR_max*0.65, slope*CR_max*0.25, 'Below line:\nSE-unit-cost lower', fontsize=11)
ax.text(CR_max*0.65, slope*CR_max*0.85, 'Above line:\nRO-unit-cost lower', fontsize=11)

# Feasibility-case notes (symbolic)
notes = (
    "Feasibility depends on (N_G, N_A, T*):\n"
    "F1: both SE & RO feasible → choose by line.\n"
    "F2: only SE feasible → choose SE.\n"
    "F3: only RO feasible → choose RO.\n"
    "F4: neither pure feasible but hybrid feasible → choose Hybrid;\n"
    "    endpoint α* chosen by which side of line."
)
ax.text(0.02, 0.98, notes, transform=ax.transAxes, va='top', fontsize=9)

ax.set_xlabel(r'$C_R$ (ground $\to$ Moon cost per launch)')
ax.set_ylabel(r'$c_E$ (elevator cost per ton, surface $\to$ apex)')
ax.set_title(r'Figure B: Cost partition in $(C_R,c_E)$ (symbolic break-even line)')
ax.set_xlim(0, CR_max)
ax.set_ylim(0, slope*CR_max*1.2)
ax.grid(True, linestyle='--', linewidth=0.5)
ax.legend(loc='upper left')

plt.tight_layout()
path_B = "/mnt/data/figure_B_cost_partition.png"
plt.savefig(path_B, dpi=200)
plt.close(fig)

paths_A, path_B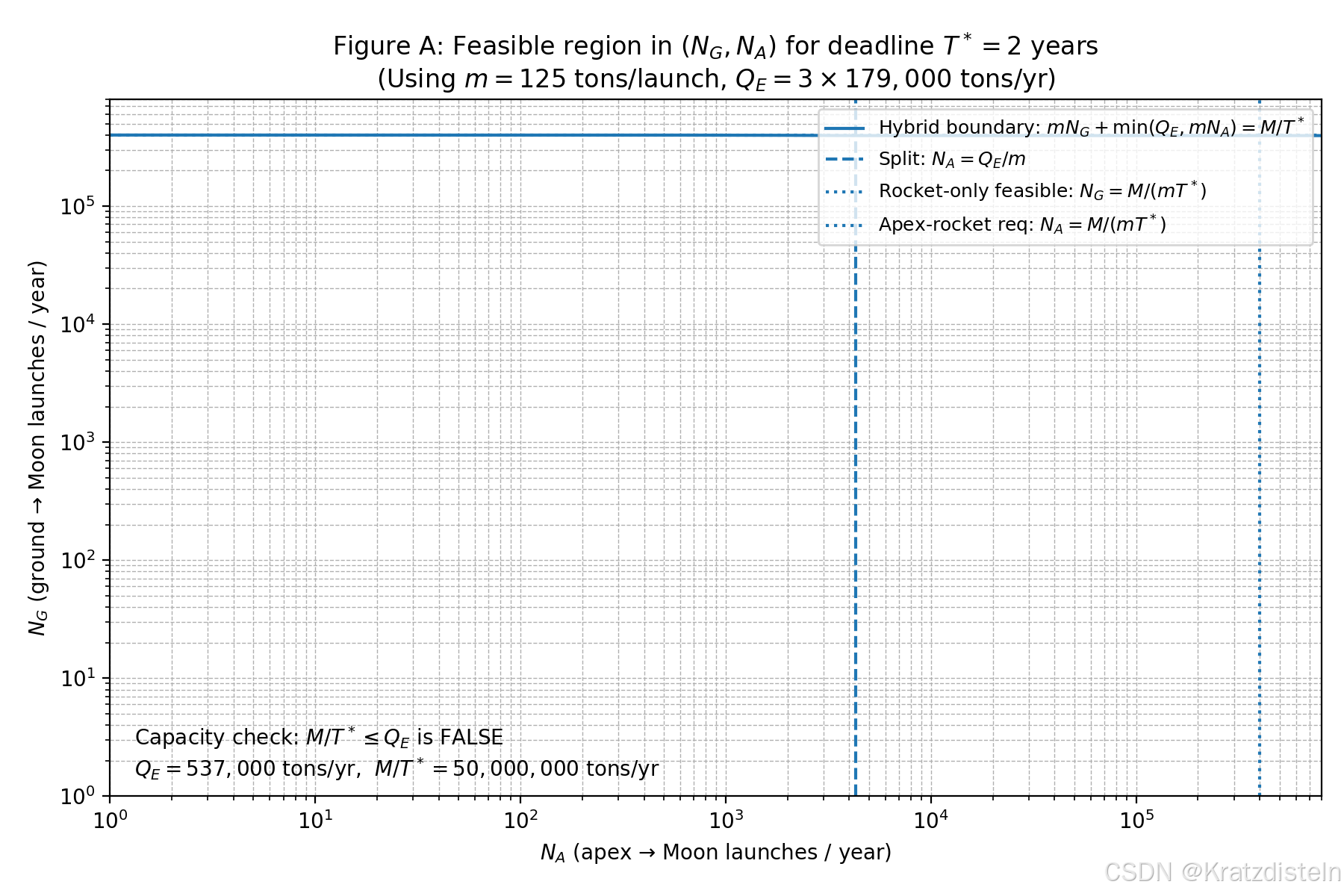

---

import numpy as np

import matplotlib.pyplot as plt

Given / assumed parameters for plotting

M = 1e8 # tons

H = 3

Q_h = 179000 # tons/year per harbour

Q_E = H * Q_h # total elevator nominal throughput (tons/year)

m = 125 # tons/launch (representative within [100,150])

Tstars = [1, 2, 3] # years

NA0 = Q_E / m # boundary NA = Q_E/m

def plot_A(Tstar, outpath):

req = M / (m * Tstar) # required launches/year if only rockets (or total launches if in region I)

# Prepare NA grid for boundary curve (piecewise)
NA_vals = np.logspace(0, np.log10(req*2), 600)  # from 1 to 2*req
boundary_NG = np.where(NA_vals < NA0, np.maximum(req - NA_vals, 1e-9), np.maximum(req - NA0, 1e-9))

fig = plt.figure(figsize=(9, 6))
ax = plt.gca()

# Hybrid feasibility boundary
ax.plot(NA_vals, boundary_NG, label=r'Hybrid boundary: $mN_G+\min(Q_E,mN_A)=M/T^*$')

# Split NA = Q_E/m
ax.axvline(NA0, linestyle='--', label=r'Split: $N_A=Q_E/m$')

# Rocket-only feasibility (independent of N_A)
ax.axhline(req, linestyle=':', label=r'Rocket-only feasible: $N_G=M/(mT^*)$')

# Apex rocket requirement line (independent of N_G)
ax.axvline(req, linestyle=':', label=r'Apex-rocket req: $N_A=M/(mT^*)$')

# Capacity check annotation
D = M / Tstar
cap_ok = D <= Q_E
ax.text(0.02, 0.02,
        (r'Capacity check: $M/T^*\leq Q_E$ is ' + ('TRUE' if cap_ok else 'FALSE')
         + '\n' + rf'$Q_E={Q_E:,.0f}$ tons/yr,  $M/T^*={D:,.0f}$ tons/yr'),
        transform=ax.transAxes, fontsize=10, va='bottom')

ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel(r'$N_A$ (apex $\to$ Moon launches / year)')
ax.set_ylabel(r'$N_G$ (ground $\to$ Moon launches / year)')
ax.set_title(rf'Figure A: Feasible region in $(N_G,N_A)$ for deadline $T^*={Tstar}$ years'
             + f'\n(Using $m={m}$ tons/launch, $Q_E=3\\times179,000$ tons/yr)')

ax.set_xlim(1, req*2)
ax.set_ylim(1, req*2)
ax.legend(fontsize=9, loc='upper right')
ax.grid(True, which='both', linestyle='--', linewidth=0.5)

plt.tight_layout()
plt.savefig(outpath, dpi=200)
plt.close(fig)

Generate A plots for T*=1,2,3

paths_A = []

for T in Tstars:

p = f"/mnt/data/figure_A_Tstar_{T}.png"

plot_A(T, p)

paths_A.append§

Figure B: cost partition in (C_R, c_E)

lambda_discount = 0.5 # example; user can change

slope = (1 - lambda_discount) / m # c_E = slope * C_R

CR_max = 1e10

CR_vals = np.linspace(0, CR_max, 400)

cE_line = slope * CR_vals

fig = plt.figure(figsize=(9, 6))

ax = plt.gca()

ax.plot(CR_vals, cE_line, label=rf'Break-even: c E = 1 − λ m C R c_E=\frac{{1-\lambda}}{{m}}C_R cE=m1−λCR (here λ = l a m b d a d i s c o u n t \lambda={lambda_discount} λ=lambdadiscount, m = m m={m} m=m)')

Region labels

ax.text(CR_max0.65, slope CR_max0.25, 'Below line:\nSE-unit-cost lower', fontsize=11)
ax.text(CR_max 0.65, slopeCR_max0.85, 'Above line:\nRO-unit-cost lower', fontsize=11)

Feasibility-case notes (symbolic)

notes = (

"Feasibility depends on (N_G, N_A, T*):\n"

"F1: both SE & RO feasible → choose by line.\n"

"F2: only SE feasible → choose SE.\n"

"F3: only RO feasible → choose RO.\n"

"F4: neither pure feasible but hybrid feasible → choose Hybrid;\n"

" endpoint α* chosen by which side of line."

)

ax.text(0.02, 0.98, notes, transform=ax.transAxes, va='top', fontsize=9)

ax.set_xlabel(r' C R C_R CR (ground → \to → Moon cost per launch)')

ax.set_ylabel(r' c E c_E cE (elevator cost per ton, surface → \to → apex)')

ax.set_title(r'Figure B: Cost partition in ( C R , c E ) (C_R,c_E) (CR,cE) (symbolic break-even line)')

ax.set_xlim(0, CR_max)

ax.set_ylim(0, slopeCR_max 1.2)

ax.grid(True, linestyle='--', linewidth=0.5)

ax.legend(loc='upper left')

plt.tight_layout()

path_B = "/mnt/data/figure_B_cost_partition.png"

plt.savefig(path_B, dpi=200)

plt.close(fig)

paths_A, path_B

已帮你把 **图A（(N_G,N_A) 可行域）**和 图B（(C_R,c_E) 成本分区）画出来了（按你之前的符号定义）。我这里用一个代表性载荷 (m=125) tons/launch（在题面 100--150 区间内）来画图；你要换成 100 或 150 我也可以立刻重画一版。

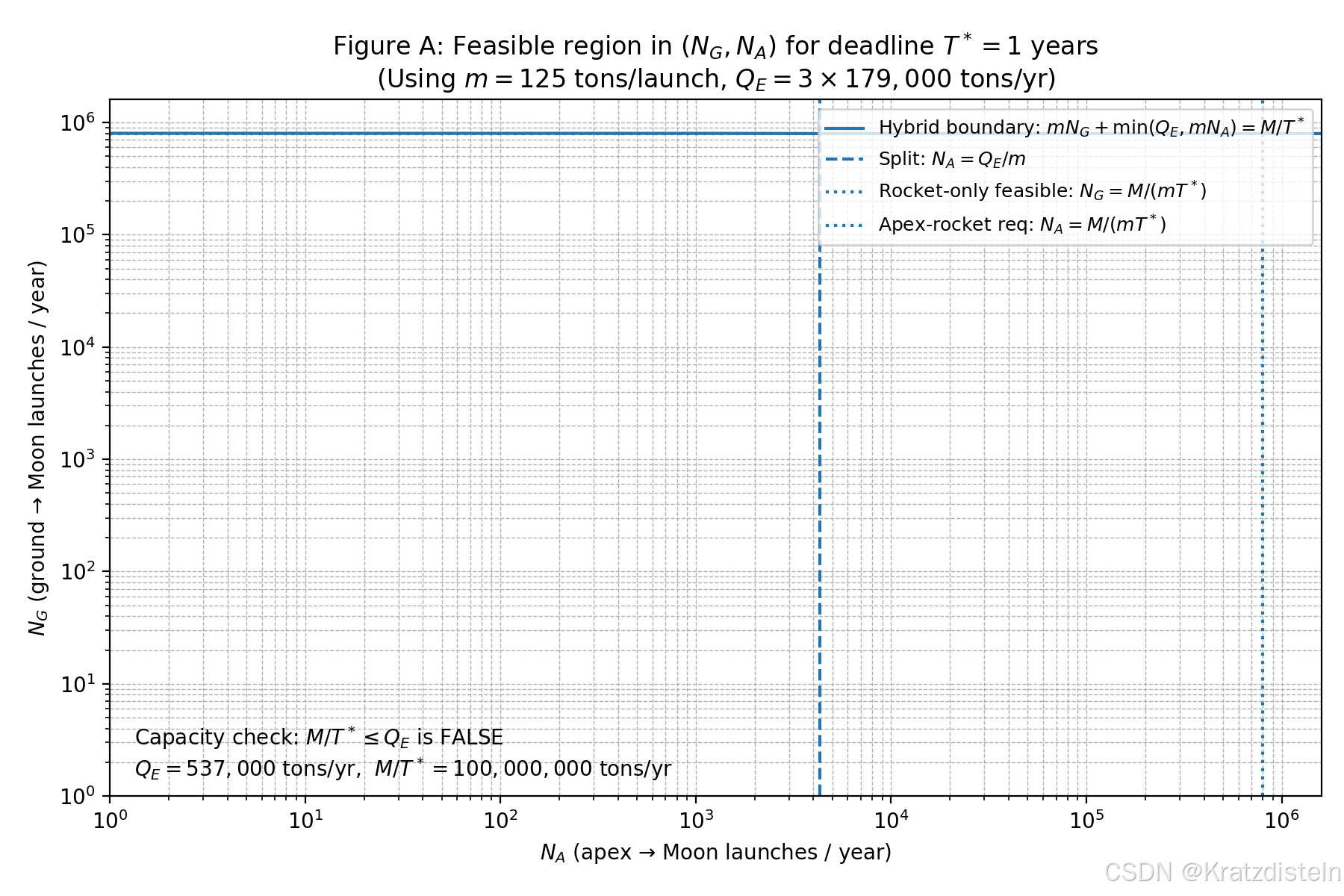
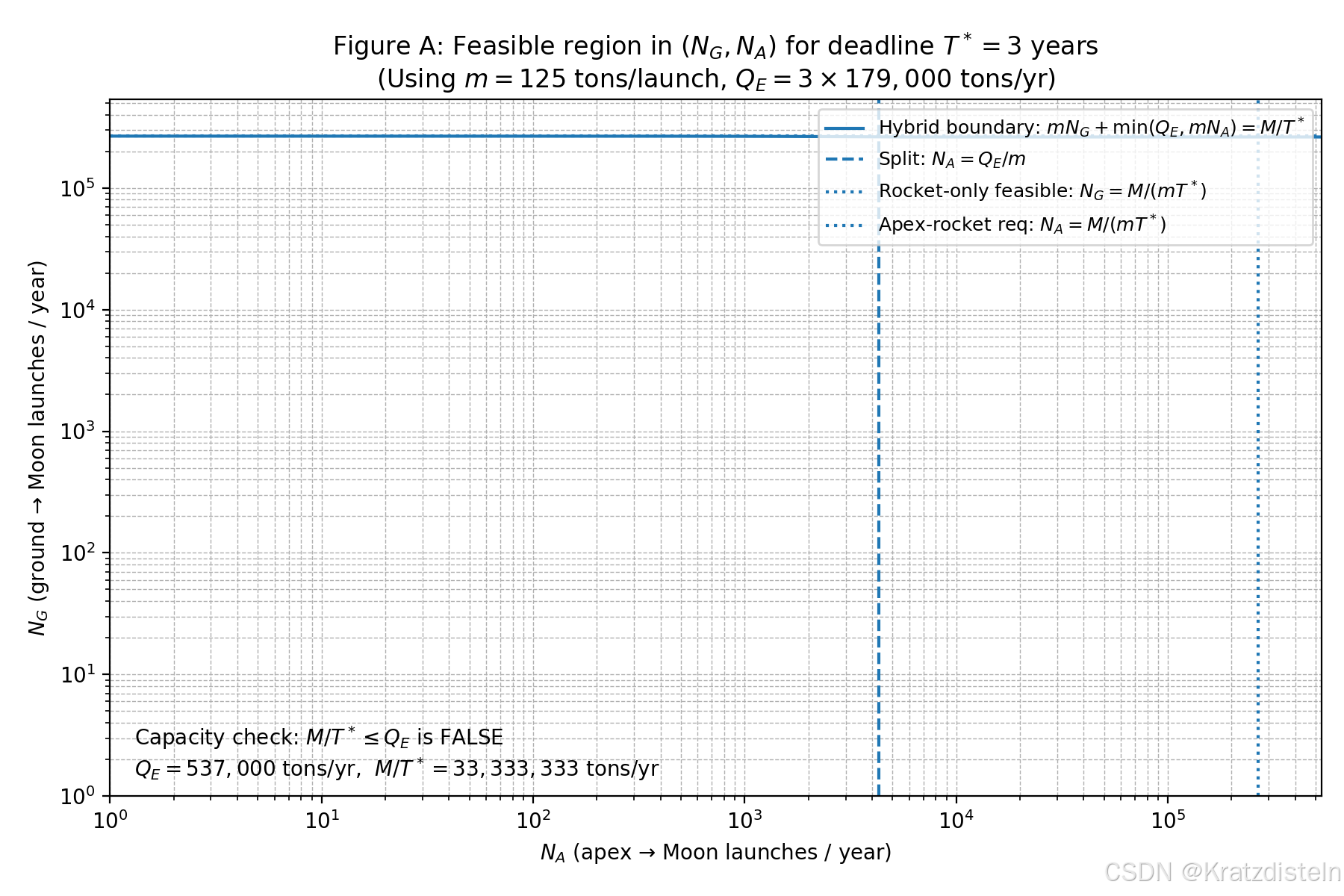
图A：((N_G,N_A)) 可行域（分别对应 (T^*=1,2,3) 年）

• 含：竖线 (N_A=Q_E/m)，混合可行边界，纯火箭阈值 (N_G=M/(mT^))，以及 apex 火箭阈值 (N_A=M/(mT^))
• 坐标用了 log-log，方便同时看清"很小的 (Q_E/m)"和"很大的 (M/(mT^*))"

下载 Figure A (T*=1)

下载 Figure A (T*=2)

下载 Figure A (T*=3)

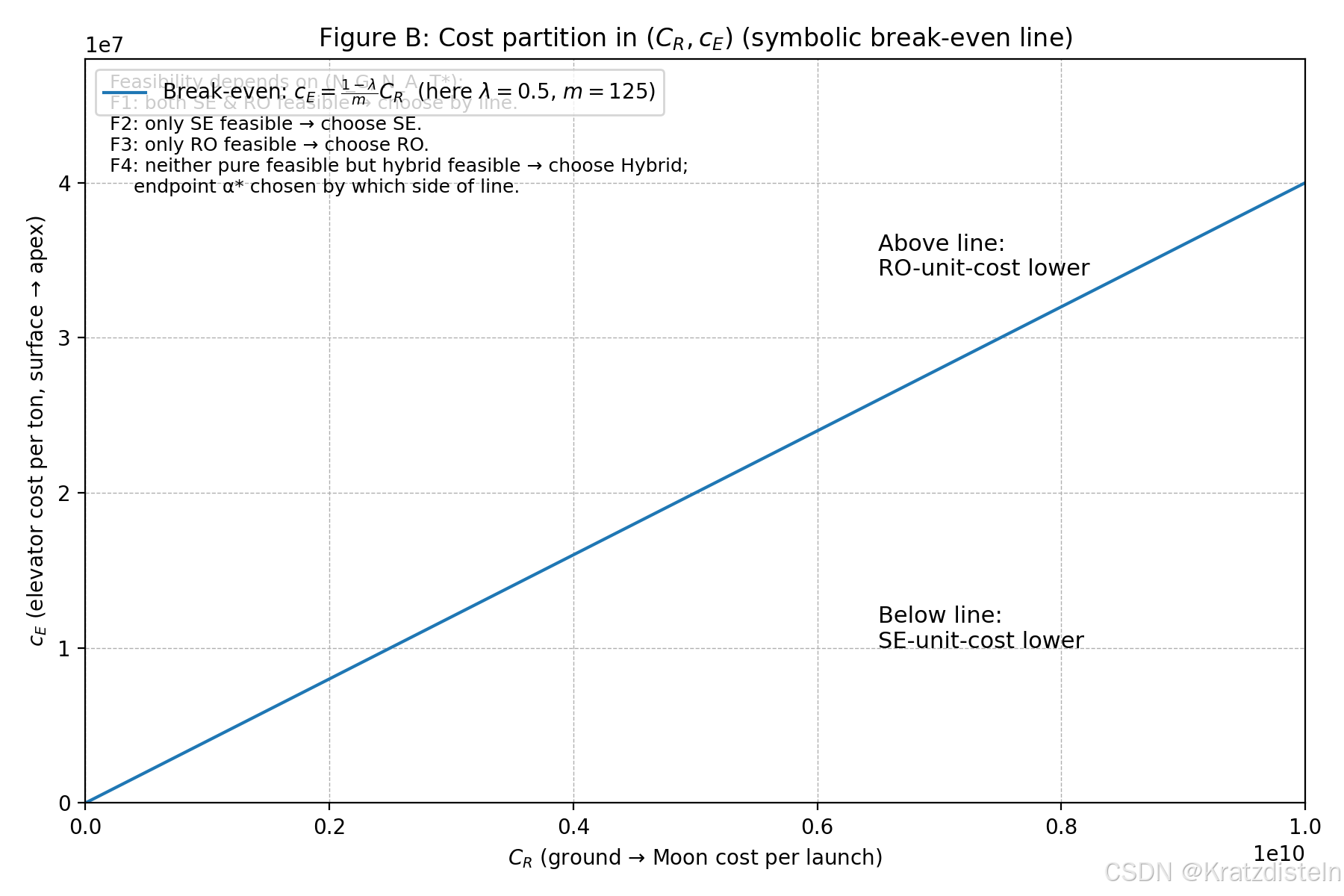
图B：((C_R,c_E)) 分区图

• 画了分割线：[
  c_E=\frac{1-\lambda}{m}C_R
  ]
• 我用示例 (\lambda=0.5)（体现"apex 用更少 fuel"）和 (m=125) 来画；线下 SE 单位成本更低，线上 RO 更低；并在图里标了 F1--F4 的可行性判定提示（最优方案最终要结合 ((N_G,N_A,T^*)) 的可行性）。

下载 Figure B