Zero-Shot Accurate mmWave Antenna Array Calibration in the Wild

文章目录

- 摘要
- [CCS 概念](#CCS 概念)
- 关键词
[1 INTRODUCTION](#1 INTRODUCTION)
[2 PRIMER](#2 PRIMER)
[3 EICAL 设计](#3 EICAL 设计)
[4 IMPLEMENTATION AND BASELINES](#4 IMPLEMENTATION AND BASELINES)
[6 RELATED WORK](#6 RELATED WORK)
[7 CONCLUSION AND FUTURE WORK](#7 CONCLUSION AND FUTURE WORK)

摘要

毫米波天线阵列校准是制造过程中必不可少但又繁琐且昂贵的过程，用于捕获相控阵中的非理想特性，从而获得用于精确且稳定的波束导向的码本。不幸的是，制造商提供的用于在给定方向集合上控制波束的预定义码本，并不支持各种毫米波通信、传感和安全应用所需的任意波束形状。

为了创建任意波束方向图，首先需要找到所使用的特定相控阵的未知校准向量（the unknown calibration vector）。在本文中，我们介绍了 EiCal ，这是一种新颖的零样本技术，它利用制造商提供的波束成形码本，以零成本（即无需额外测量，i.e., with no additional measurements）提取校准向量。

其核心思想是，可以通过对给定码本进行适当设计的特征分解来获得未知的期望校准向量。我们在一个 60 GHz 毫米波阵列上实验验证了 EiCal 在两种场景下的有效性：

使用压缩伪随机波束的角度估计（angle estimation using compressive pseudorandom beams），
以及波束和零陷的同时导向（simultaneous steering of beams and nulls）。

我们的结果也指出了制造商校准过程中潜在的简化可能。

CCS 概念

硬件 → \rightarrow → 波束成形。

关键词

校准，天线阵列，毫米波，零样本

1 INTRODUCTION

相控阵在毫米波（mmWave）通信和传感中起着至关重要的作用 [14, 15]。毫米波频段的短载波波长使得具有大量阵元的天线阵列的小型化成为可能，而射频集成电路（RFIC）的设计通过将单个射频链路连接到天线阵元来简化，其中每个阵元具有独立的幅度/相位控制。这种阵列可以形成针对不同通信和传感设置优化的各种波束方向图，包括用于在特定方向提供高增益的定向波束、用于减少干扰的零陷、以及用于压缩感知的伪随机波束。为了合成给定的波束方向图，幅度/相位控制需要知道不同阵列阵元的相对几何结构以及相对本地振荡器相位。

虽然阵列阵元的物理几何结构通常是精确已知的（例如，具有等间距阵元的线性阵列），但对于许多射频设计而言，阵元之间的相对相位往往不太可预测（例如，由于连接 RFIC 和天线的电路板中的传输线长度变化），因此需要校准。例如，制造商可能会根据在消声室中进行的大量受控测量提供一个"码本"，码本中的每个条目指定了向给定方向形成波束所需的幅度/相位控制。然而，此类码本并不会告诉我们如何创建其他类型的波束方向图，例如

在波束之外形成零陷（forming nulls in addition to beams），
或者具有可用于感知的伪随机相位的压缩波束方向图（compressive beam patterns with pseudorandom phases which can be used for sensing）。

压缩波束方向图 (Compressive Beam Patterns)：由上述伪随机相位生成的波束形状，看起来是杂乱无章的，这种方向图被称为"压缩波束"。

对于几何结构已知的天线阵列，如果天线单元之间的幅度/相位关系（在施加任何控制信号之前）保持稳定，且不存在诸如'随方向变化的互耦'等难以建模的效应，那么我们只需确定一个能够概括这些关系的单一校准向量（a single calibration vector），即可合成任意类型的波束方向图（in order to synthesize any such beam pattern）。

事实上（Indeed），缺乏此类校准信息是利用实地已部署的基础设施进行各种传感应用的主要瓶颈之一。虽然原则上（While，in principle）可以在实地利用专用的移动节点辅助校准（尽管这需要通过详尽且耗时的测量），但环境的不可控本质（例如多径效应、轻微的天线未对准）在实践中阻碍了校准参数的精确估计。

在本文中，我们要

表明可以通过特征分析从现有码本中提取准确的校准向量，而无需额外的测量 ，并在商用现货（COTS） 60 GHz 60 \text{ GHz} 60 GHz 硬件（见第 4 节）上通过实验证明，这种校准向量确实足以产生除特定方向上的简单波束成形之外的各种波束方向图。
虽然我们在特定的硬件平台上演示了我们的校准方法，但它适用于任何已知足够多波束成形码本条目的相控阵（it applies to any phased array for which a large enough number of beamforming codebook entries are known）。
我们的结果还表明，可以显著减少码本条目的数量，而不会影响我们从中提取的校准向量的质量。
图 1 描绘了我们提出的"零样本"方法（我们称之为 EiCal，which we term EiCal）与最先进技术之间的关系概览。

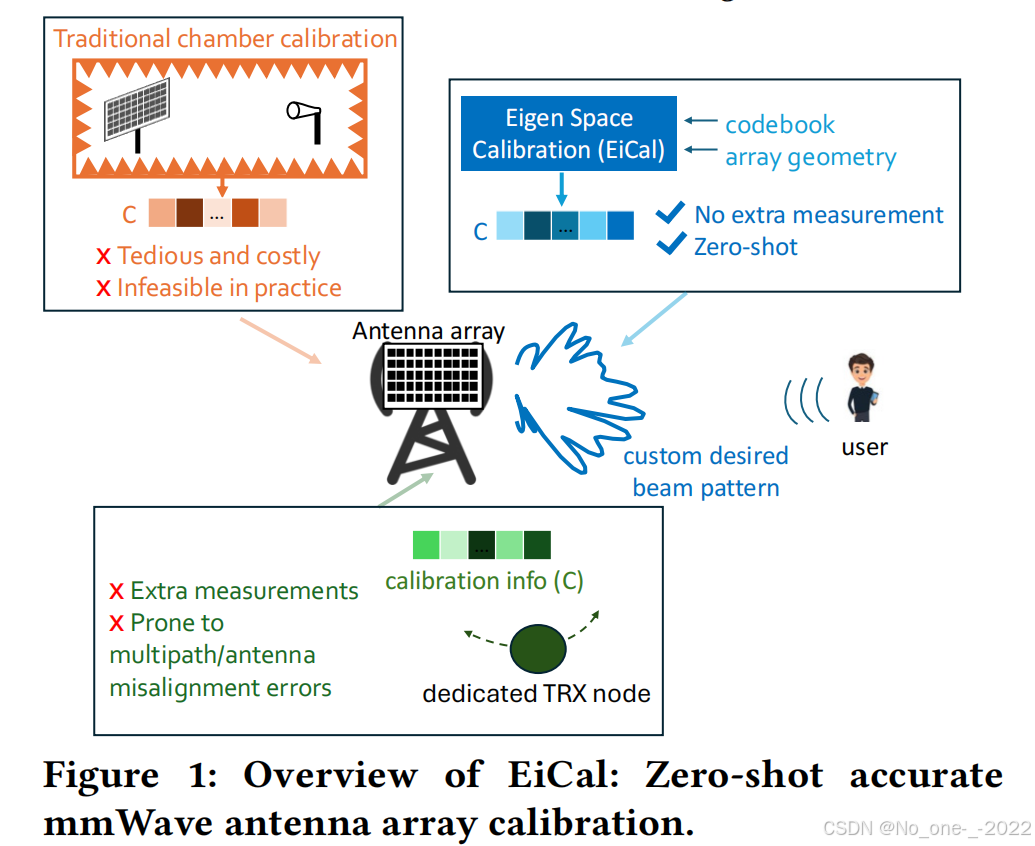
图 1 解读：EiCal 与传统校准方法的对比

这张图展示了为了让天线阵列生成自定义波束 （针对用户优化），三种获取校准信息（C）的不同途径：

传统暗室校准 (左上)

方法：在专业的微波暗室中进行精密测量。

缺点：
* 成本高、耗时 ：需要昂贵设备和漫长测试。
* 不切实际 ：无法对已经安装在户外的基站进行拆卸校准。

基于专用节点的实地校准 (下方)

方法：在户外使用专门的收发设备（如无人机）在基站附近进行测量。

缺点：
* 需要额外测量 ：费时费力。
* 精度差 ：户外环境复杂，多径效应 （反射）和天线未对准 会导致校准结果错误。

EiCal 方法 (右上 - 本文提出)

方法：纯计算方法，无需新测量。

输入：利用厂家已有的 "标准码本" + 已知的 "阵列几何结构"。

核心：通过特征空间分析直接算出来校准向量。

优势：
* 零样本 (Zero-shot) ：不需要采集任何新数据。
* 零成本 ：无需额外测量，避开了环境干扰。

总结：EiCal 克服了传统方法的昂贵和环境干扰问题，通过数学方法实现了快速、精准的校准。

我们将我们的贡献总结如下：

我们提出了 EiCal，这是一种通过对现有码本进行特征分析，以计算高效的方式获取阵列校准向量的方法，且不需要任何额外的测量。
我们通过实验证明，由 EiCal 生成的单一校准向量确实足以合成各种波束方向图，包括用于压缩角度估计和零陷形成的波束方向图。我们使用 60 GHz 60 \text{ GHz} 60 GHz Sivers 无线电 [9] 作为我们的评估平台。
我们的实验表明，对于所考虑的压缩感知和零陷形成任务，EiCal 的表现优于基准方法，例如最近提出的需要额外测量的校准技术。
我们展示了校准精度在所需的码本条目数量上很快达到平台期（the accuracy of calibration quickly plateaus in the number of codebook entries needed）。这表明（This indicates）所需的校准测量数量可以比目前提供的数量显著减少，从而可能减轻制造过程中的校准负担。

2 PRIMER

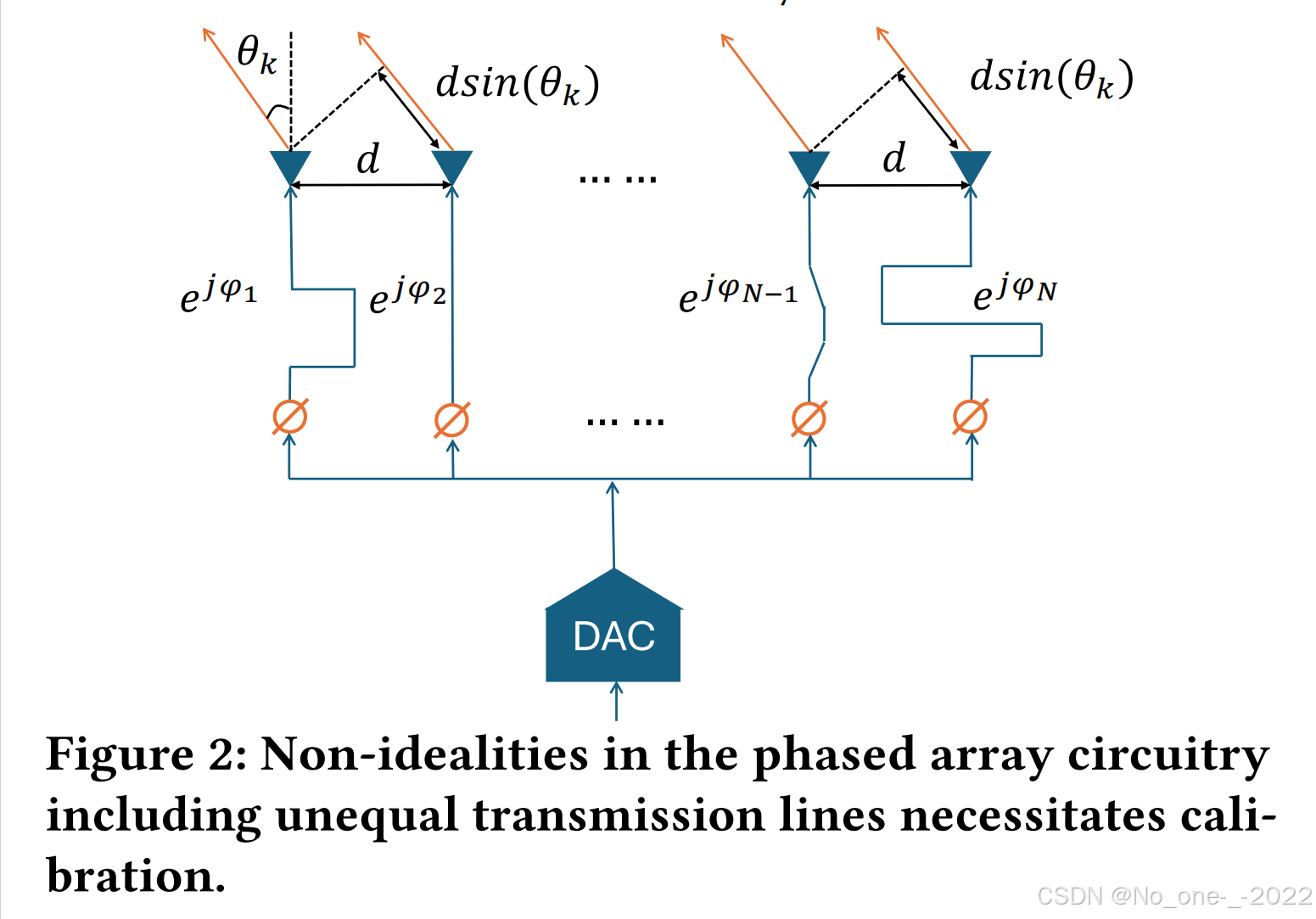
我们现在讨论我们的校准模型。虽然该方法是通用的，但我们以均匀间隔阵元的线性阵列为例进行说明，如图 2 所示。对于一个已校准的阵列，为了在角度 θ k \theta_k θk（相对于宽边）方向上产生相干相加的方向图，我们必须在相邻阵元之间施加 Ω k = 2 π d sin ⁡ ( θ k ) λ \Omega_k = \frac{2\pi d \sin(\theta_k)}{\lambda} Ωk=λ2πdsin(θk) 的相对相移。这对应于一个 N × 1 N \times 1 N×1 的 标称导向矢量

a Nominal ( Ω k ) = [ 1 e − j Ω k ... e − j ( N − 1 ) Ω k ] T , Ω k = 2 π d sin ⁡ ( θ k ) λ , (1) \mathbf{a}_{\text{Nominal}}(\Omega_k) = \left[ 1 \ e^{-j\Omega_k} \ \dots \ e^{-j(N-1)\Omega_k} \right]^T , \ \Omega_k = \frac{2\pi d \sin(\theta_k)}{\lambda} , \tag{1} aNominal(Ωk)=[1 e−jΩk ... e−j(N−1)Ωk]T, Ωk=λ2πdsin(θk),(1)

其中 N N N 是天线阵元的数量。

因此，为了将波束导向 K K K 个预定义的角度 { θ 1 , θ 2 , ... , θ K } \{\theta_1, \theta_2, \dots, \theta_K\} {θ1,θ2,...,θK}，理想校准阵列的 标称码本 （nominal codebook）由 N × K N \times K N×K 矩阵给出

A Nominal = [ a Nominal ( Ω 1 ) a Nominal ( Ω 2 ) ⋯ a Nominal ( Ω K ) ] , (2) \mathbf{A}{\text{Nominal}} = [\mathbf{a}{\text{Nominal}}(\Omega_1) \ \mathbf{a}{\text{Nominal}}(\Omega_2) \ \cdots \ \mathbf{a}{\text{Nominal}}(\Omega_K)] , \tag{2} ANominal=[aNominal(Ω1) aNominal(Ω2) ⋯ aNominal(ΩK)],(2)

然而，在实践中，制造商提供的码本与上述理论计算不同。这种差异背后的原因是多方面的：

首先，大多数实际的移相器分辨率有限，因此需要量化。
其次，电路中的缺陷（imperfections in the circuitry），例如（such as）不同天线与其对应的移相器之间的传输线长度不相等，会引入公式 ( 2 ) (2) (2) 中未考虑的额外相移。

因此，对于用于波束成形的先验未校准阵列，典型的过程是制造商通过在微波暗室中进行大量测量来确定预定义的期望导向码本的权重矢量。令 a Advertised ( Ω k ) \mathbf{a}_{\text{Advertised}}(\Omega_k) aAdvertised(Ωk) 表示通过此类测量确定的沿方向 θ k \theta_k θk 导向所需的权重矢量。对于预定义的导向方向集合 { θ 1 , θ 2 , ... , θ K } \{\theta_1, \theta_2, \dots, \theta_K\} {θ1,θ2,...,θK}，公开码本（advertised codebook）将这些导向矢量作为列包含在内：

A Advertised = [ a Advertised ( Ω 1 ) a Advertised ( Ω 2 ) ⋯ a Advertised ( Ω K ) ] (3) \mathbf{A}{\text{Advertised}} = [\mathbf{a}{\text{Advertised}}(\Omega_1) \ \mathbf{a}{\text{Advertised}}(\Omega_2) \ \cdots \ \mathbf{a}{\text{Advertised}}(\Omega_K)] \tag{3} AAdvertised=[aAdvertised(Ω1) aAdvertised(Ω2) ⋯ aAdvertised(ΩK)](3)

然后，这会与客户共享并嵌入到天线前端的控制单元中。如果我们要合成仅在量化方向集合中的定向波束（synthesizing directional beams in a quantized set of directions），这样的码本提供了一种完全通用的方法来对阵列硬件中的非理想特性进行建模，不仅包括阵列阵元间幅度和相位参考的变化，还包括更复杂的效应，如阵元间的互耦，这实际上可能取决于到达/离开的方向 [1]。然而，公开码本并没有提供合成更丰富的波束方向图所需的信息，例如压缩感知（compressive sensing）或零陷形成（null formation）所需的波束方向图。

我们的校准方法基于这样一个假设：对于我们使用的商用现货（COTS）硬件中采用的简单线性阵列，我们可以忽略互耦等效应，并且主要的非理想特性（dominant non-idealities）是阵元间幅度和相位参考的变化，以及公开码本中权重的量化所带来的不准确性。这一假设得到了我们实验结果的验证，结果表明我们的方法准确地复现了公开码本的条目，并实现了准确的压缩感知和零陷形成。在该模型下，校准可以通过找到一个单一的 N N N 阵元校准矢量 C ∈ C N × 1 \mathbf{C} \in \mathbb{C}^{N \times 1} C∈CN×1 来完成，其中用于在第 k k k 个方向上进行波束成形的公开权重向量（the advertised weight vector），与对应的标称权重向量（the corresponding nominal weight vector）之间，存在如下关系

a Advertised ( Ω k ) = Q ( α k C ⊙ a Nominal ( Ω k ) ) , k = 1 , . . . , K (4) \mathbf{a}{\text{Advertised}}(\Omega_k) = Q(\alpha_k \mathbf{C} \odot \mathbf{a}{\text{Nominal}}(\Omega_k)) , \ k=1, ..., K \tag{4} aAdvertised(Ωk)=Q(αkC⊙aNominal(Ωk)), k=1,...,K(4)

其中

⊙ \odot ⊙ 表示逐元素乘积，
α k \alpha_k αk 表示可以随不同波束方向变化的任意复标量，
Q ( ⋅ ) Q(\cdot) Q(⋅) 是对其输入的相位进行量化的量化函数。例如，商用的 60 GHz 60 \text{ GHz} 60 GHz 阵列具有 6 位移相器 [9]。

在下一节中，我们提供了一种计算高效的方法，用于在给定公开码本 A Advertised \mathbf{A}_{\text{Advertised}} AAdvertised 的情况下估计校准矢量 C \mathbf{C} C。一旦完成这一步，为了合成期望的波束方向图，我们使用理想化阵列模型获得标称权重矢量，然后使用校准矢量对其进行调整。当然，最终的波束方向图是这个合成的波束方向图与单个阵元的辐射方向图的乘积。

最终方向图 = 单个天线的方向图 × 阵列合成方向图 \text{最终方向图} = \text{单个天线的方向图} \times \text{阵列合成方向图} 最终方向图=单个天线的方向图×阵列合成方向图

The final beam pattern is, of course, a product of the synthesized beam pattern with the radiation pattern for a single element.

3 EICAL 设计

在本节中，我们推导 EiCal，这是一种零样本、无测量的策略，用于提取校准向量。根据第 2 节中定义的 A Advertised \mathbf{A}{\text{Advertised}} AAdvertised 和 A Nominal \mathbf{A}{\text{Nominal}} ANominal 矩阵的第 k k k 列，可以由公式 (4) 得到如下关系：

a Advertised ( Ω k ) = α k C ⊙ a Nominal ( Ω k ) + n k , k = 1 , . . . , K (5) \mathbf{a}{\text{Advertised}}(\Omega_k) = \alpha_k \mathbf{C} \odot \mathbf{a}{\text{Nominal}}(\Omega_k) + \mathbf{n}_k, \ k = 1, ..., K \tag{5} aAdvertised(Ωk)=αkC⊙aNominal(Ωk)+nk, k=1,...,K(5)

其中 n k \mathbf{n}_k nk 是一个 N × 1 N \times 1 N×1 的噪声向量，用于对量化噪声和任何其他模型失配进行建模。因此，我们可以通过从公开的阵列响应中"剔除"标称阵列响应，来恢复 K K K 个带有噪声和缩放的校准向量副本，如下所示：

a Advertised ( Ω k ) ⊙ a Nominal ∗ ( Ω k ) = α k C + n ~ k , k = 1 , . . . , K (6) \mathbf{a}{\text{Advertised}}(\Omega_k) \odot \mathbf{a}{\text{Nominal}}^*(\Omega_k) = \alpha_k \mathbf{C} + \tilde{\mathbf{n}}_k, \ k = 1, ..., K \tag{6} aAdvertised(Ωk)⊙aNominal∗(Ωk)=αkC+n~k, k=1,...,K(6)

其中 n ~ k = n k ⊙ a Nominal ∗ ( Ω k ) \tilde{\mathbf{n}}_k = \mathbf{n}k \odot \mathbf{a}{\text{Nominal}}^*(\Omega_k) n~k=nk⊙aNominal∗(Ωk) 是变换后的噪声向量。

在 (6) 中获得的 K K K 个带有噪声和缩放的校准向量副本，很容易看出是由公开码本与标称码本的复共轭进行逐元素相乘所获得的矩阵的列：

P = A Advertised ⊙ A Nominal ∗ = ( α 1 C . . . . α K C ) + N ~ (7) \mathbf{P} = \mathbf{A}{\text{Advertised}} \odot \mathbf{A}{\text{Nominal}}^* = (\alpha_1 \mathbf{C} .... \alpha_K \mathbf{C}) + \tilde{\mathbf{N}} \tag{7} P=AAdvertised⊙ANominal∗=(α1C....αKC)+N~(7)

其中噪声矩阵 N ~ \tilde{\mathbf{N}} N~ 包含变换后的噪声向量 n ~ k , k = 1 , . . . , K \tilde{\mathbf{n}}_k, k = 1, ..., K n~k,k=1,...,K 作为列。

忽略 (7) 中的噪声项， P \mathbf{P} P 中的列都是同一向量 C \mathbf{C} C 的倍数，对应于一个秩为 1 的矩阵。因此，我们可以通过有噪声矩阵 P \mathbf{P} P 的秩 1 近似来获得 C \mathbf{C} C 的估计值。矩阵的最佳秩 1 近似是 P \mathbf{P} P 的奇异值分解 (SVD) 中的最大"本征模" [5] 。 N × K N \times K N×K 矩阵 P \mathbf{P} P 的 SVD 形式为（takes the form）：

P = U diag { σ 1 , . . . , σ m } V H = ∑ i = 1 m σ i u i v i H (8) \mathbf{P} = \mathbf{U} \text{diag}\{\sigma_1, ..., \sigma_m\} \mathbf{V}^H = \sum_{i=1}^m \sigma_i \mathbf{u}_i \mathbf{v}_i^H \tag{8} P=Udiag{σ1,...,σm}VH=i=1∑mσiuiviH(8)

其中 m = min ⁡ ( N , K ) m = \min(N, K) m=min(N,K)， σ i ≥ 0 \sigma_i \geq 0 σi≥0 是按降序排列的奇异值， U \mathbf{U} U 是包含左奇异向量 { u i , i = 1 , . . . , m } \{\mathbf{u}_i, i=1, ..., m\} {ui,i=1,...,m} 作为列的 N × m N \times m N×m 正交矩阵， V \mathbf{V} V 是包含右奇异向量 { v i , i = 1 , . . . , m } \{\mathbf{v}_i, i=1, ..., m\} {vi,i=1,...,m} 作为列的 K × m K \times m K×m 正交矩阵，其中 x H \mathbf{x}^H xH 表示向量或矩阵 x \mathbf{x} x 的复共轭转置。 P \mathbf{P} P 的最佳秩 1 近似已知为 [5]

P ^ = σ 1 u 1 v 1 H (9) \widehat{\mathbf{P}} = \sigma_1 \mathbf{u}_1 \mathbf{v}_1^H \tag{9} P =σ1u1v1H(9)

与 (7) 比较并忽略噪声，我们看到 u 1 \mathbf{u}_1 u1 应该与 C \mathbf{C} C 成比例，而 v 1 H \mathbf{v}_1^H v1H 应该与 ( α 1 , . . . , α K ) (\alpha_1, ..., \alpha_K) (α1,...,αK) 成比例。注意到（Noting that）比例常数对于校准和波束成形并不重要，因此我们可以将校准向量估计为第一个左奇异向量：

C ^ = u 1 (10) \widehat{\mathbf{C}} = \mathbf{u}_1 \tag{10} C =u1(10)

一旦估计出校准向量，就可以通过使用理论阵列模型首先找到相应的标称权重向量 ( w des,nom ) (\mathbf{w}_{\text{des,nom}}) (wdes,nom)，然后逐元素应用校准向量来生成任意期望的波束方向图，如下所示：

w des,cal = C ^ ⊙ w des,nom (11) \mathbf{w}{\text{des,cal}} = \widehat{\mathbf{C}} \odot \mathbf{w}{\text{des,nom}} \tag{11} wdes,cal=C ⊙wdes,nom(11)

如此获得的权重向量将根据相控阵控制的硬件实现进行进一步量化。

我们将在第 5 节中展示，即使仅使用原始公开码本中的少量波束，EiCal 的校准过程也是准确的。校准质量随着更高分辨率的移相器（产生更小的量化噪声）而提高。最后，我们要强调的是，与需要新测量的传统校准方法相比，EiCal 不需要额外的实验来提取校准向量。相反，它完全依赖于已知的码本（即使它包含很少的波束）以及基于天线和传播理论计算出的权重向量。因此，EiCal 提供了一种便捷的方法，可以为各种通信、传感和安全场景生成精确的任意形状的波束方向图。

4 IMPLEMENTATION AND BASELINES

我们通过使用商用现货毫米波阵列来验证和评估 EiCal 的校准精度。具体来说，我们使用的是 Sivers EVK06002 板 [9]，这是一款具有 16 × 4 16 \times 4 16×4 天线的 60 GHz 60 \text{ GHz} 60 GHz 毫米波无线电。制造商为每个阵列提供了一个包含 63 个权重向量的码本，这些向量可用于创建 63 个不同的定向波束，主瓣在方位角方向上跨越 -45 到 45 度，步长约为 1.5 度。移相器具有 6 位相位分辨率，两个阵列阵元之间的距离略小于 λ 2 \frac{\lambda}{2} 2λ，这表明一旦已知其几何结构，EiCal 就有能力推广到任何相控阵。

Automated Radiation Mapping Setup。为了评估目的，我们测量了几个自定义波束的辐射方向图，并将其与校准后的仿真方向图进行了比较。

我们的测量设置如图 3a 所示。在右侧，展示了发射号角天线，它直接面向 Sivers 无线电。号角天线由信号发生器馈电。在接收（RX）侧，我们将 Sivers 无线电安装在旋转台上，详情见图 3b。旋转台从 -90 度旋转到 90 度，步长为 2 度。接收端直接连接到频谱分析仪。在所有实验中，中心频率均为 60.48 GHz 60.48 \text{ GHz} 60.48 GHz。我们在发射端（TX）和接收端（RX）周围放置了吸波材料（未显示），以消除任何潜在的多径。在这些实验中，我们评估了接收相控阵上的校准精度，但同样的方法也适用于发射阵列。

Calibration Baselines：我们将 EiCal 与以下基准进行了比较：

(a) 无校准向量。此基准不使用任何校准向量来生成波束方向图。
(b) Nulli-Fi [7]。该基准通过进行多次测量来找到校准向量，使得每轮中除了两个天线外，其余所有天线都关闭。在每一轮中，改变两个开启天线之间的相对相位，并记录接收到的信号幅度。显然，当两个天线变为同相时，幅度将最大化，而为实现这一点所施加的额外相移推断出了所需的相位校准。通过重复相同的过程多轮（By repeating the same procedure multiple rounds），可以获得（one can obtain）所有天线的相对相移并形成校准向量。事实上，该方案的主要缺点是它需要在受控设置中进行详尽的测量。

Testing EiCal in Forming Desired Radiation Patterns：我们评估了 EiCal 在实际设置中精确生成自定义期望波束方向图的性能：

(i) 压缩波束成形。压缩波束成形涉及伪随机天线权重向量的选择（产生看起来随机的辐射方向图），并已被证明是毫米波网络中快速路径发现和到达角估计的有效方法 [8]。然而，压缩感知的角度估计精度取决于天线校准。因此，我们使用图 3c 所示的设置进行实验。测量是在一个具有 3 m 3 \text{ m} 3 m 收发距离的大型开放空间中进行的。两个 Sivers 无线电分别充当发射机（Tx）和接收机（Rx），它们分别使用全向波束和压缩感知波束。Tx 无线电连接到任意波形发生器（arbitrary waveform generator，AWG），Rx 无线电连接到示波器。
(ii) 零陷导向。零陷导向在非预期用户（或干扰源）的方向上产生零陷，同时将主瓣导向目标用户的方向。它已被证明在多用户网络中对最小化干扰和最大化信号与噪声及干扰比（SINR）非常有用 [2]。然而，零陷导向的精度依赖于天线阵列校准。因此，我们通过调查 EiCal 在零陷性能中的作用来评估其性能。

模拟波束操控在包括无线通信、传感和安全在内的几个领域的过往文献中得到了充分探索。现有的工作要么

依赖制造商提供的码本以创建预定义的波束方向图 [11]，
要么操控码本以创建有限数量的新波束方向图（例如，双瓣波束）[12]，
或者进行详尽的校准以按需生成任意方向图 [6]。

现有的阵列校准工作包括暴力测量，例如改变两个天线的相位 [7]、将阵列设置为波束导向模式 [10]、或者测量反转每个阵元的相位对幅度和相位的影响 [13]。不幸的是，此类方案既耗时又难以扩展。更重要的是，它们不适用于校准已经部署在野外的阵列，因为进行受控测量（例如，没有多径且精确对准）并不简单。我们实现了这样一种最近的方法 [7] 作为基准，并表明 EiCal 的性能优于它。

与这些先前的工作相比，EiCal 是准确的、零样本（zero-shot）的且无需实验的。EiCal 仅将阵列的几何结构和制造商提供的定向码本作为输入。我们在各种任务（包括压缩感知和零陷导向）中的广泛仿真和实验演示表明，EiCal 在保持轻量级和可扩展性（while being lightweight and scalable）的同时实现了准确的性能。

7 CONCLUSION AND FUTURE WORK

本文提出了 EiCal ，这是一种精确的零样本校准方案，它仅利用阵列几何结构的知识和制造商公开的定向码本，通过特征分析来获得精确的校准向量，而 无需额外的测量。
我们在商用现货 60 GHz 60 \text{ GHz} 60 GHz 阵列上对 EiCal 进行了实验评估，表明我们的校准向量能够精确生成除指定方向上的基本波束成形之外的各种波束方向图，包括用于定位应用的伪随机压缩波束，以及用于干扰管理的零陷导向。
我们的发现还表明，我们可以大幅减少码本中的条目数量，而不会损害从中提取出的校准向量的质量，从而可能减轻制造过程中的校准负担。
未来的工作可以探索将此方法扩展到其他相控阵几何结构和硬件配置。此外，将这种校准方法与自适应波束成形技术相结合，可以在动态通信环境中提供更大的灵活性和性能。