【PQ分解法潮流计算(matlab版)】

程序名称##

PQ分解法潮流计算(matlab版)

算法说明

PQ分解法，也称为快速解耦潮流法，是牛顿-拉夫逊法潮流计算的一种极重要的改进和简化算法。它的核心思想是利用电力系统特有的物理特性，对牛顿法的修正方程进行合理近似和解耦，从而大幅减少计算量和内存需求，提高计算速度。
1.核心思想及条件分析

有功功率主要与节点电压相角有关：当两条母线之间的电压相角差发生变化时，其传输的有功功率会发生显著变化。

无功功率主要与节点电压幅值有关：当母线电压的幅值发生变化时，其产生的无功功率会发生显著变化。

高压电网的"特性"：线路的电阻远小于电抗，因此有：支路两端电压相角差通常很小。各节点电压幅值与其额定值相差不大，可近似认为 ≈ 1.0 p.u.。

基于以上假设，可以将牛顿法中描述（有功不平衡-相角变化）和（无功不平衡-电压幅值变化）之间关系的雅可比矩阵常数化和解耦。
2.从牛顿法到PQ分解法的推导

牛顿法的修正方程为：

ΔPΔQ\]=\[HN JL\]\[Δθ ΔV/V\] \\begin{bmatrix} \\Delta P \\newline \\Delta Q \\end{bmatrix} = \\begin{bmatrix} H \& N \\newline\\ J \& L \\end{bmatrix} \\begin{bmatrix} \\Delta \\theta \\ \\newline \\Delta V / V \\end{bmatrix} \[ΔPΔQ\]=\[H JNL\]\[Δθ ΔV/V

步骤1：解耦

在高压电网中认为有功变化对电压幅值不敏感，无功变化对相角不敏感。方程变为：

ΔP=HΔθ\]\[ΔQ=L(ΔVV)\] \[ \\Delta P = H\\Delta \\theta \] \\newline\[ \\Delta Q = L \\left( \\frac{\\Delta V}{V} \\right) \] \[ΔP=HΔθ\]\[ΔQ=L(VΔV)

步骤2：常数化

进一步利用高压网络特性对 H 和 L 进行简化：

对于 H 矩阵：忽略对地支路和变压器非标准变比的影响，并假设 ≈ 1，可推导出 H 矩阵的元素等于节点导纳矩阵的虚部（电纳）的负值。

对于 L 矩阵：做类似简化，发现 L 矩阵的元素也近似等于节点导纳矩阵的虚部。

于是得到两个独立的常数方程：

ΔP=−B′Δθ\]\[ΔQ=−B′′(ΔVV)\] \[ \\Delta P = -B' \\Delta \\theta \] \\newline\[ \\Delta Q = -B''\\left( \\frac{\\Delta V}{V} \\right)\] \[ΔP=−B′Δθ\]\[ΔQ=−B′′(VΔV)

B' 和 B'' 都是常数矩阵，由系统导纳矩阵的虚部构成。

通常，在建立 B' 时，忽略所有与有功功率相关的元件影响；在建立 B'' 时，忽略变压器非标准变比和线路充电电容的影响。

3.算法流程

数据准备与初始化：输入网络参数、节点数据，设置平衡节点和PQ、PV节点。将除了平衡节点外的所有电压幅值初始化为1.0 p.u.，相角初始化为0。

形成常数矩阵：根据网络拓扑和参数，形成并三角分解（LU分解）常数矩阵 B' 和 B''。这一步只需做一次。

迭代计算（解耦交替求解）：

a) P-θ 迭代：

用当前电压值计算各节点的有功功率不平衡量。

求解方程，得到电压相角修正量。

更新各节点的电压相角。

b) Q-V 迭代：

用更新后的相角值计算各PQ节点的无功功率不平衡量。

求解方程，得到电压幅值修正量。

更新各PQ节点的电压幅值。

收敛判断：检查所有节点的和是否都小于给定的收敛精度ε。如果满足，则迭代结束，计算平衡节点功率和线路功率；否则，返回步骤3进行下一次迭代。

程序功能(对象)

适用于任意大小的纯交流电网,支持节点和支路的增删；
适用于接入多个风电、光伏等分布式电源；
子函数包含：节点导纳矩阵计算，雅克比矩阵计算(n-1+m维)，B'、B''矩阵计算；
程序输出：各个节点电压相角、支路首末端潮流及损耗、发电机功率、最大迭代收敛次数；
误差分析：输出形式对标matpower内runpf()函数，误差<10^-3；

程序函数说明

主程序：Test_PQ_PowerFlow
输入算例子程序：截图包含的所有case文件
节点导纳子程序：createYbus文件
雅克比矩阵子程序：Jacobi文件

程序计算步骤及流程图

参数初始化，读取网络参数，在此标幺化

ac_data = case30;
ac_baseMVA = ac_data.baseMVA;
ac_bus = ac_data.bus;
ac_branch = ac_data.branch;
ac_gen = ac_data.gen; %电网数据
ac_dg = ac_data.dg; %%电网数据
形成节点导纳矩阵n*n维

Ybus = createYbus(ac_baseMVA, ac_bus, ac_branch);
构建B' 和 B'' 都是常数矩阵

temp_branch = ac_branch;
temp_branch(:, 5) = zeros(nl, 1); %%忽略接地支路电纳
temp_branch(:, 3) = zeros(nl, 1); %%忽略支路电阻
Bp = imag( createYbus(ac_baseMVA, ac_bus, ac_branch));
%Bp = imag( makeYbus(ac_baseMVA, temp_bus, temp_branch) );%%交流子系统的Bp
Bp = Bp([pq; pv], [pq; pv]); %%剔除平衡节点将pq放置矩阵前列(n-1)(n-1)
%Bpp = imag( makeYbus(ac_baseMVA, ac_bus, ac_branch) ); %%交流子系统的Bpp
Bpp = imag( createYbus(ac_baseMVA, ac_bus, ac_branch));
Bpp = Bpp(pq,pq); %B1，PQ节点mm维矩阵计算

初始化有功迭代次数、无功迭代次数以及全局迭代次数

kac = 0;
Kp = 1;
Kq = 1;

计算有功功率偏差，判断是否收敛，收敛则Kp = 0否则为1

复制代码

  dP = Pacs - real(Uacs.*conj(Ybus*Uacs));   %Psi - Ui*sum(conj(Yij*Uj))
   if max(abs(dP([pq; pv]))) <= 1e-5   %有功收敛判据
       Kp  = 0;
       if  Kq  == 0
           break  
       end
   else
      dPi_dUi = (dP([pq; pv])./Uac_m([pq; pv]));
      UD1 = diag(Uac_m([pq; pv]));
      dUac_a = inv(-UD1*Bp*UD1)*dP([pq; pv])*180/pi; %弧度转角度计算
      Uac_a([pq; pv]) = Uac_a([pq; pv]) + dUac_a; %相角修正
      Kq =1;
   end

计算无功功率偏差，判断是否收敛，收敛则Kq= 0否则为1

复制代码

  dQ =Qacs - imag(Uacs.*conj(Ybus*Uacs));    
  if max(abs(dQ(pq))) <= 1e-5  %无功收敛判据
       Kq  = 0;
       if  Kp  == 0
           break  
       end
  else
      dUac_m = -inv(Bpp)*(dQ(pq)./Uac_m(pq));  %PQ节点电压幅值变化巨大
      Uac_m(pq) = Uac_m(pq) + dUac_m;  %PQ节点幅值修正
       Kp  = 1;
  end

有功相角无功电压幅值修正方程

复制代码

    dUac_a = inv(-UD1*Bp*UD1)*dP([pq; pv])*180/pi; %弧度转角度计算
     dUac_m = -inv(Bpp)*(dQ(pq)./Uac_m(pq));  %PQ节点电压幅值变化

输出节点电压和支路功率
(Bus_V第二列为电压幅值,第三列为电压相角； S_branch第三列为Pij，S_branch第四列为Pji，S_branch第五列为支路ij损耗)

复制代码

 Ui = Bus_V(:, 2) .* exp(1j * (Bus_V(:, 3)*pi/180));
 S_branch(i , 3) = Ui(from)*conj(Ui(from))*conj(yi0(from, to))+Ui(from)*(conj(Ui(from))-conj(Ui(to)))*conj(-Ybus(from, to));
 S_branch(i , 4) =Ui(to)*conj(Ui(to))*conj(yi0(to, from))+Ui(to)*(conj(Ui(to))-conj(Ui(from)))*conj(-Ybus(to, from));
 S_branch(i , 5) = real(S_branch(i , 3)+ S_branch(i , 4));

计算流程图如下图所示

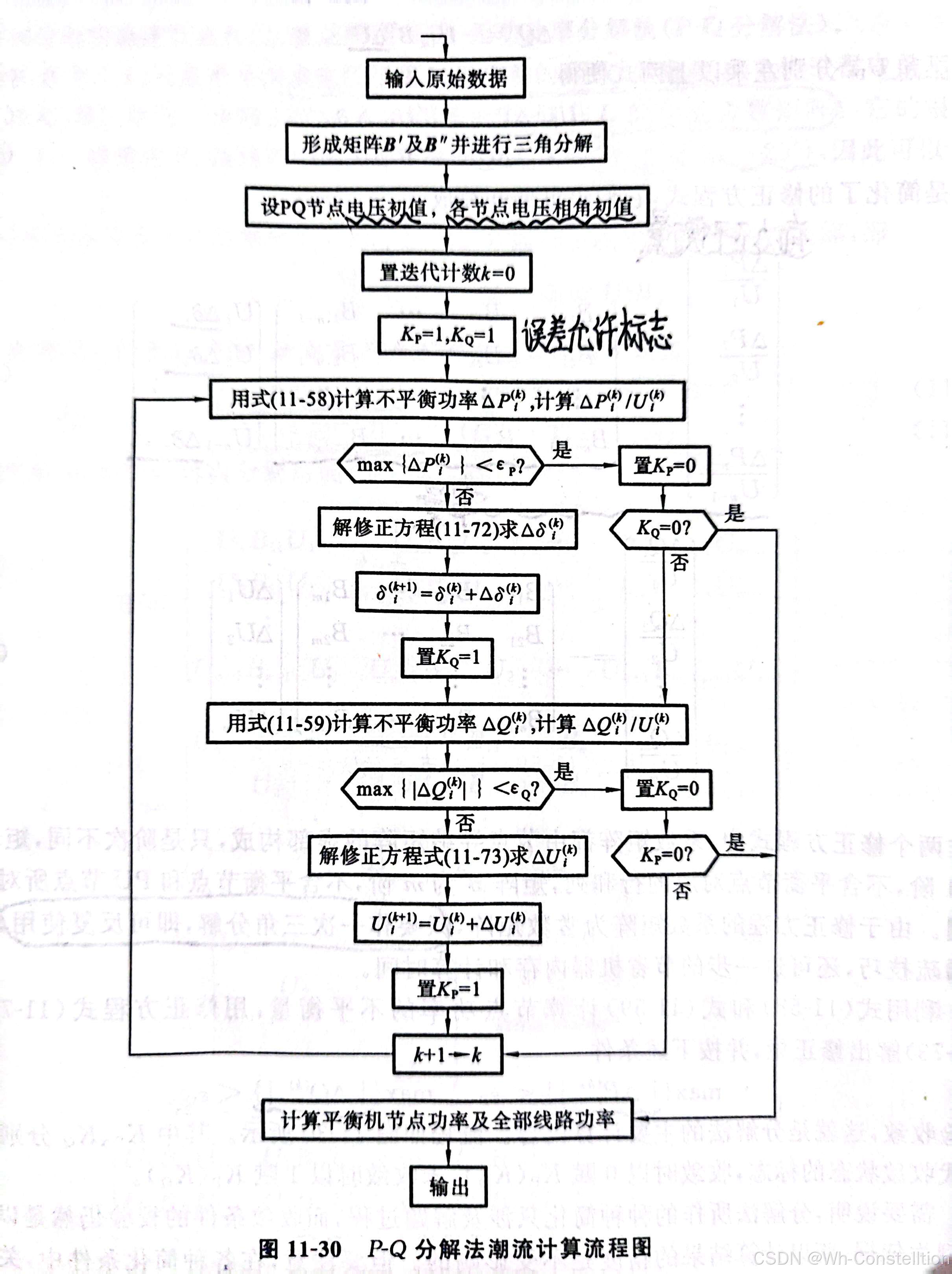
基于牛顿拉夫逊法电能损耗计算流程图

程序误差分析

，matlab版计算结果与matpower计算结果对比(结果一致)，误差主要存在于收敛精度判断

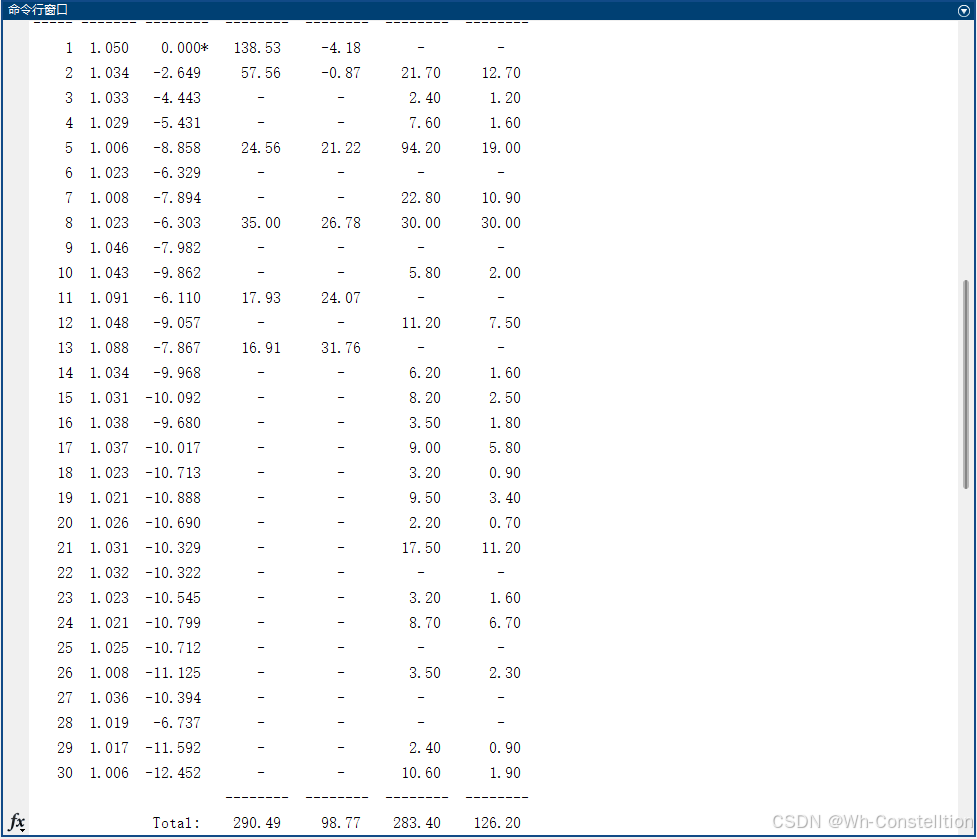
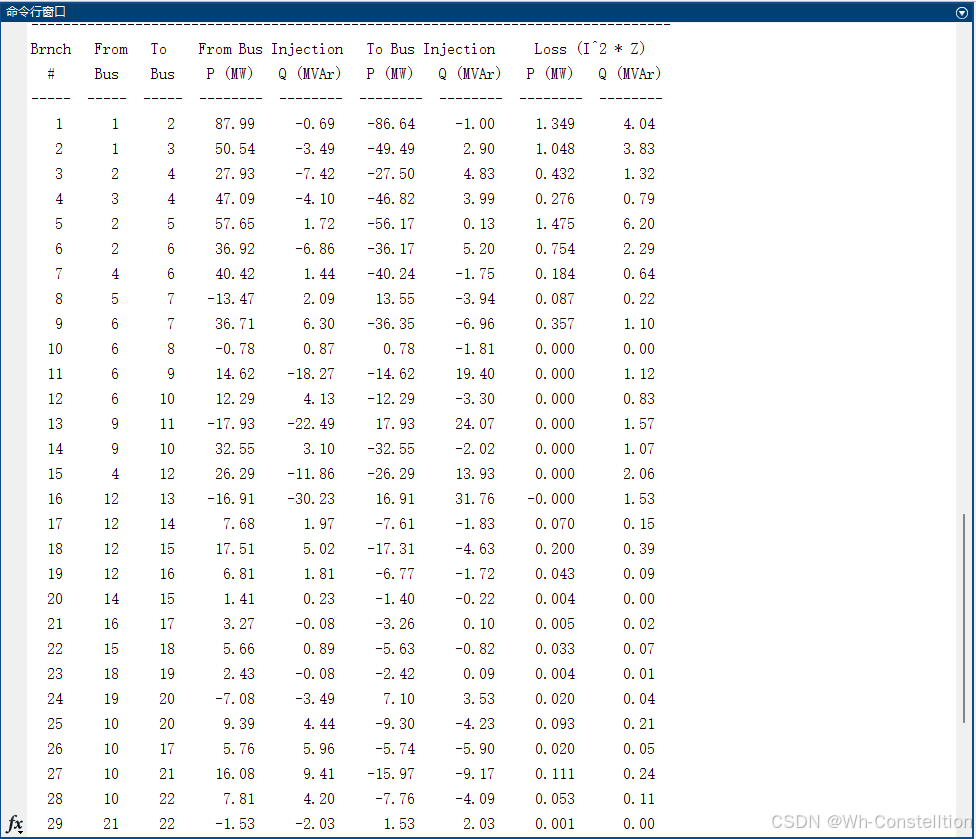
以下是程序求解的节点电压幅值相角和支路功率，可以看出偏差<10^-5，甚至更小，不过这个算法思路只能用于高压，低压不行。
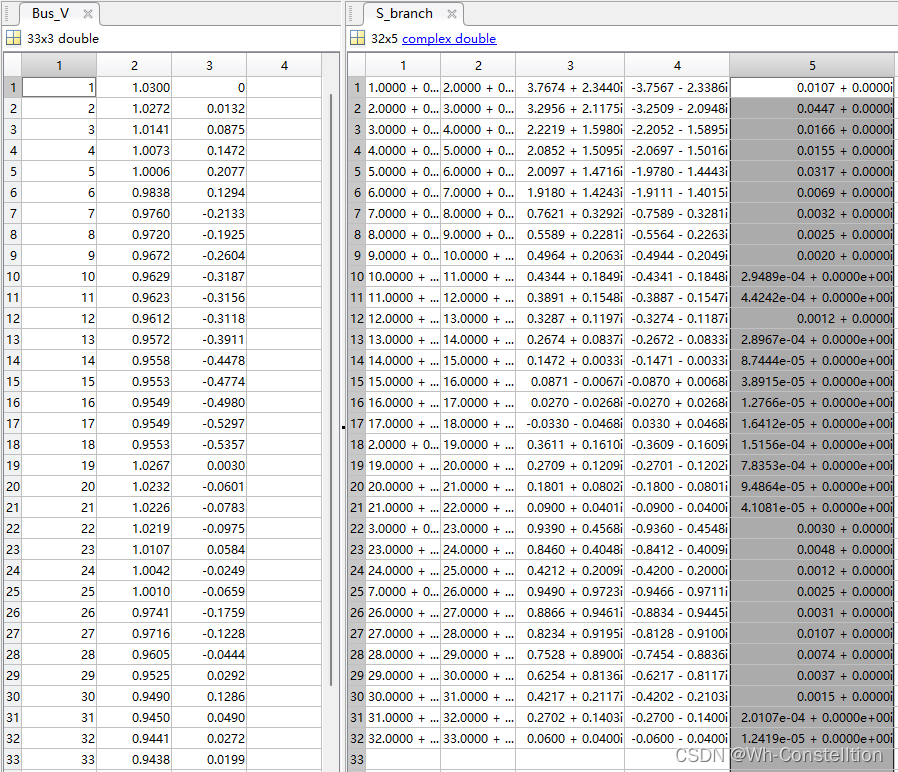
程序输出各发电机的输出功率、各条支路的首末端功率、以及各条支路的损耗情况

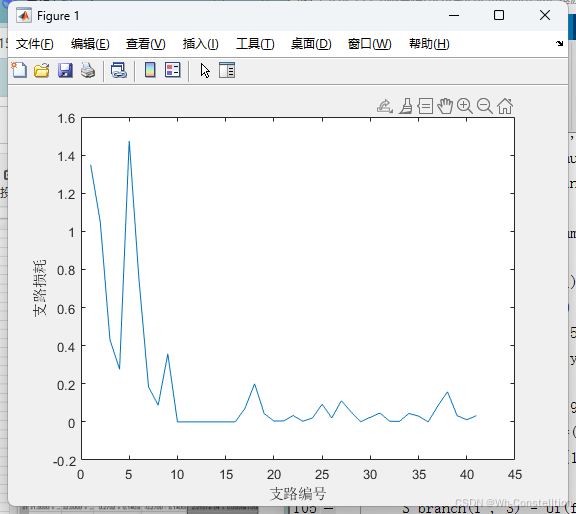
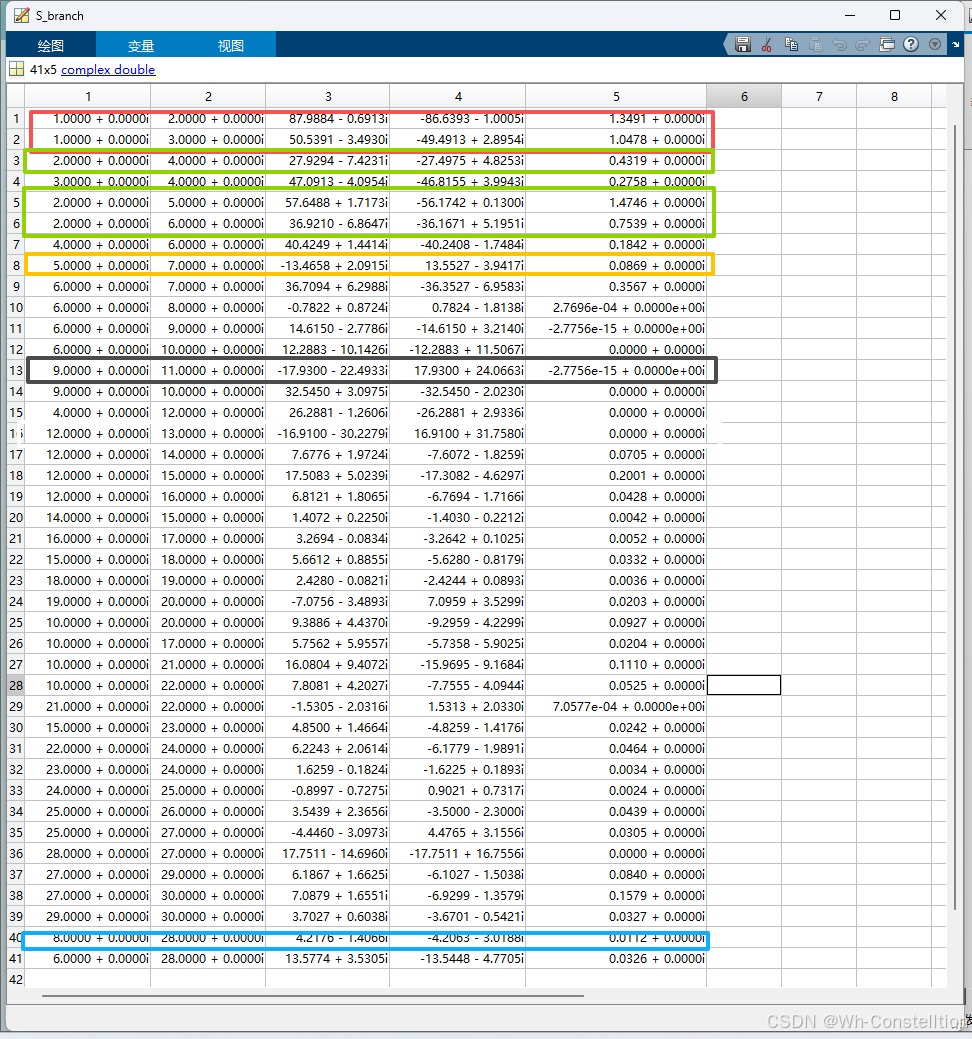
程序获取

需要完整版程序的，通用性程序请私信"深入"探讨V lemonyoungman 提供程序答疑

想要python版的也可以联系