《C语言》操作符详解

敲皮裤的代码2026-02-01 8:25

1 操作符的分类

  • 算术操作符：+ 、- 、* 、 / 、%
  • 移位操作符：<< >>
  • 位操作符：& | ^
  • 赋值操作符：= 、+= 、-= 、*= 、/= 、%= 、<<= 、>>= 、&= 、|= 、^=
  • 单目操作符：! 、++ 、-- 、& 、* 、+ 、- 、~ 、sizeof 、(类型)
  • 关系操作符：> 、 >= 、< 、<= 、== 、!=
  • 逻辑操作符：&& 、||
  • 条件操作符：? :
  • 逗号表达式：,
  • 下标引用：
  • 函数调用：( )
  • 结构成员访问：. 、 ->

上述的操作符，我们已经介绍过算术操作符、赋值操作符、逻辑操作符、条件操作符和部分的单目操作符，今天继续介绍一部分，操作符中有一些操作符和二进制有关系，我们先铺垫一下二进制和进制转换的知识。

2 二进制和进制转换

其实我们经常能听到2进制、8进制、16进制这样的讲法，那是什么意思呢？其实2进制、8进制、10进制、16进制是数值的不同表示形式而已。

比如：数值15的各种进制的表示形式：

cpp 复制代码 
15的2进制：1111
15的8进制：17
15的10进制：15
15的16进制：F

我们重点介绍一下二进制：

首先我们还是得从10进制讲起，其实10进制是我们生活中经常使用的，我们已经形成了很多常识：

  • 10进制中满10进1
  • 10进制的数字每一位都是0~9的数字组成

其实二进制也是一样的

  • 2进制中满2进1
  • 2进制的数字每一位都是0~1的数字组成

那么 1101 就是二进制的数字了。

2.1 2进制转10进制

其实10进制的123表示的值是一百二十三，为什么是这个值呢？其实10进制的每一位都是有权重的，10进制的数字从右向左是个位、十位、百位......，分别每一位的权重是 ，，...

如下图：

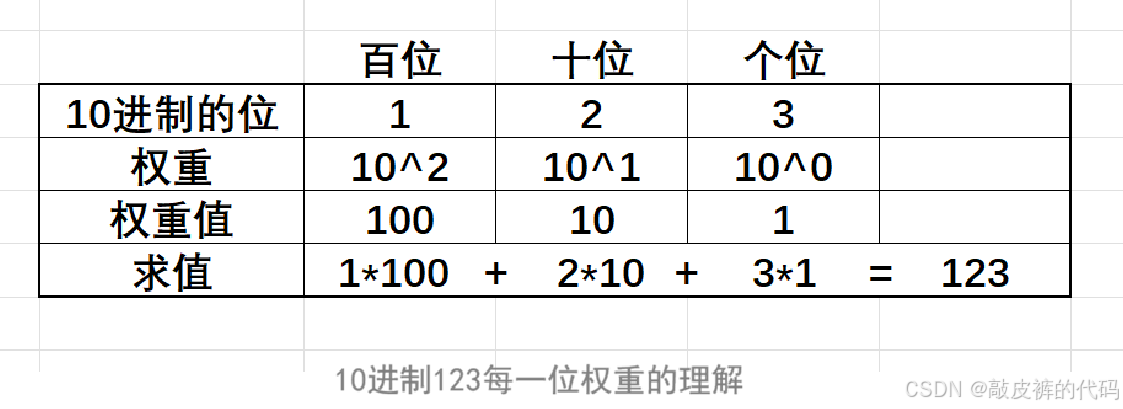
2进制和10进制是类似的，只不过2进制的每一位的权重，从右向左是：，，...

如果是2进制的1101，该怎么理解呢？

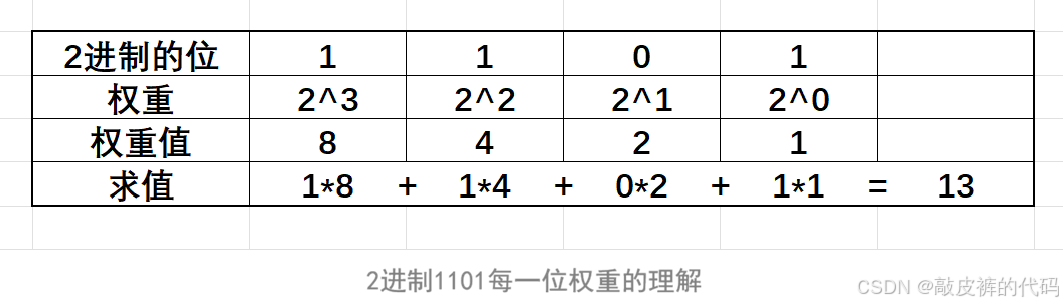
2.1.1 10进制转2进制数字

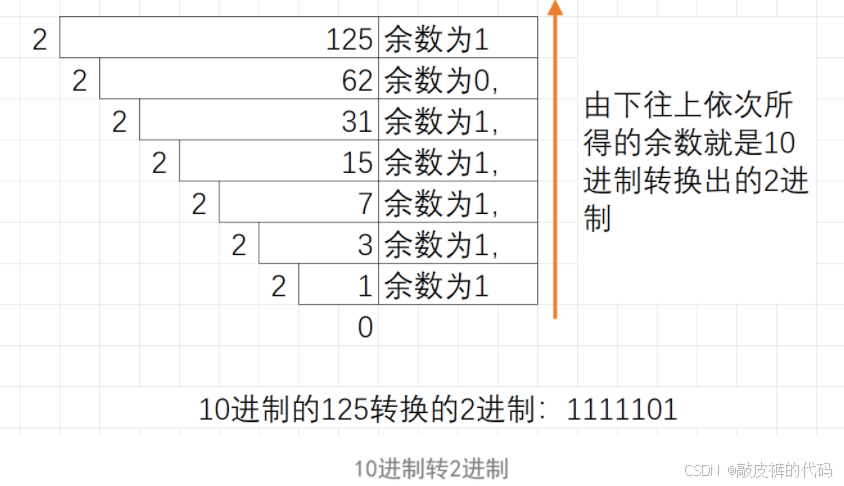
2.2 2进制转8进制和16进制

2.2.1 2进制转8进制

8进制的数字每一位是0~7的数字，各自写成2进制，最多有3个2二进制位就足够了，比如7的二进制是111，所以在2进制转8进制的时候，从2进制序列中右边低位开始向左每3个2进制位会换算一个8进制位，剩余不够3个2进制位的直接换算。

如：2进制的01101011，换成8进制：0153，0开头的数字，会被当作8进制。

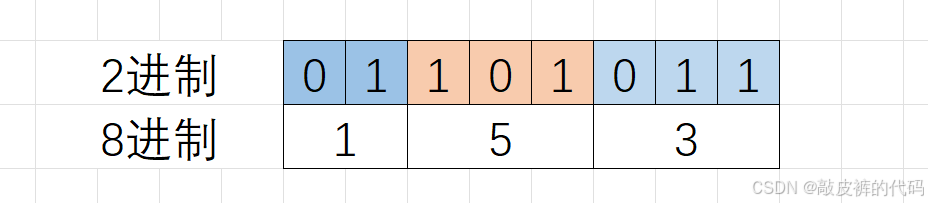
2.2.2 2进制转16进制

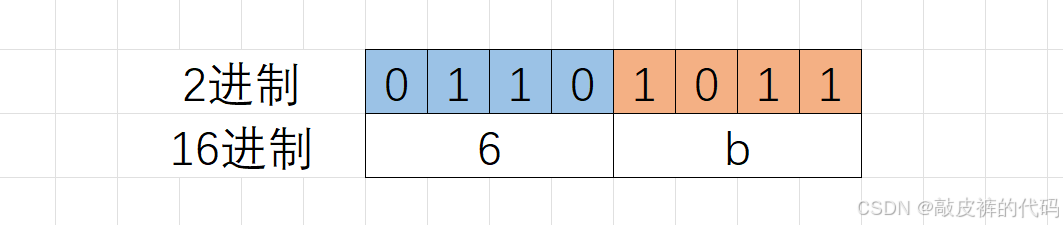
16进制的数字每一位是0~9，a~f的数字，各自写成2进制，最多有4个2进制位就足够了，比如 f 的二进制是1111，所以在2进制转16进制数的时候，从2进制序列中右边低位开始向左每4个2进制位会换算一个16进制位，剩余不够4个二进制位的直接换算。

如：2进制的01101011，换成16进制：0x6b，16进制表示的时候前面加0x。

3 原码、反码、补码

整数的2进制表示方法有三种，即原码、反码和补码。

有符号整数的三种表示方法均有符号位和数值位两部分，2进制序列中，最高位的1位是被当作符号位，剩余的都是数值位。

符号位都是用0表示"正"，用1表示"负"。

正整数的原、反、补码都相同。

负整数的三种表示方法各不相同。

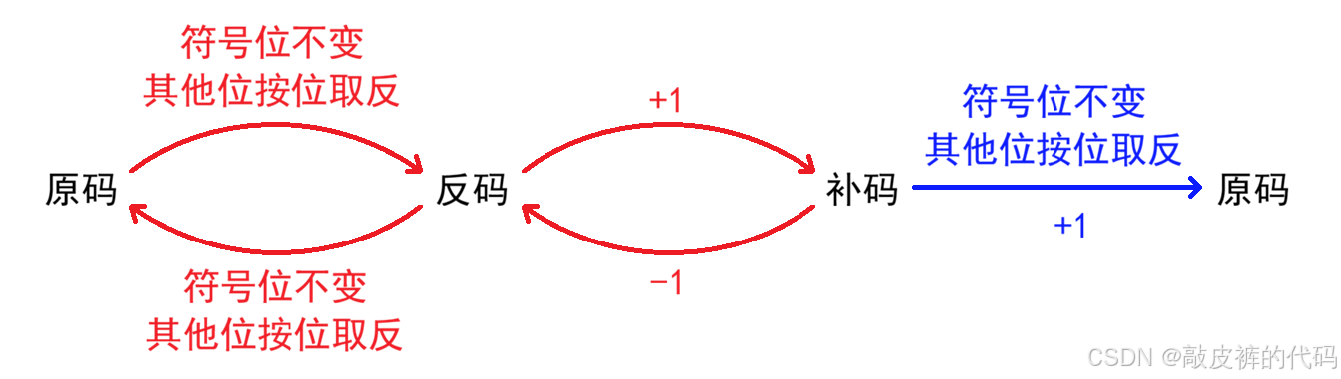
原码：直接将数值按照正负数的形式翻译成二进制得到的就是原码。

反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。

补码：反码+1就得到补码。

补码得到原码也是可以使用：取反（数值位），+1的操作。

cpp 复制代码 
int num1 = 10;    //signed int num1 = 10;
//10是存放在整型变量num1中，占4个字节 == 32bit位
00000000000000000000000000001010 - 原码
00000000000000000000000000001010 - 反码
00000000000000000000000000001010 - 补码

int num2 = -10;    //signed int num2 = -10;
//-10是存放在整型变量num2中，占4个字节 == 32bit位
10000000000000000000000000001010 - 原码
11111111111111111111111111110101 - 反码
11111111111111111111111111110110 - 补码

对于整型来说：数据存放内存中其实存放的是补码。

为什么呢？

在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理**（CPU只有加法器）**，此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

cpp 复制代码 
1-1
1+(-1)
使用原码计算
00000000000000000000000000000001 ---> 1的原码
10000000000000000000000000000001 ---> -1的原码
相加之后
10000000000000000000000000000010 ---> -2    计算结果显然不对

使用补码计算
10000000000000000000000000000001 ---> -1的原码
11111111111111111111111111111110 ---> -1的反码
11111111111111111111111111111111 ---> -1的补码
00000000000000000000000000000001 ---> 1的补码
相加之后
100000000000000000000000000000000 多出来一位 我们将它舍弃掉
00000000000000000000000000000000 ---> 0

4 移位操作符

<< 左移操作符

**>>**右移操作符

注：移位操作符的操作数只能是整数！

4.1 左移操作符

移位规则：左边丢弃，右边补0

cpp 复制代码 
#include<stdio.h>

int main()
{
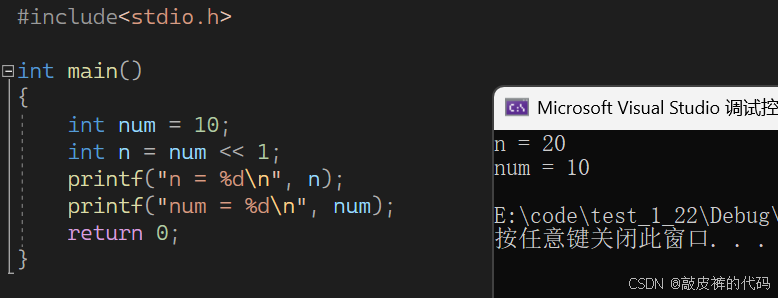
    int num = 10;
    int n = num << 1;
    printf("n = %d\n", n);
    printf("num = %d\n", num);
    return 0;
}

运行结果：

4.2 右移操作符

移位规则：首先右移运算分为两种：

  1. 逻辑右移：左边用0填充，右边丢弃
  2. 算术右移：左边用原该值的符号位填充，右边丢弃

右移到底是算术右移还是逻辑右移？这取决于编译器的实现，大部分的编译器上是算术右移。

cpp 复制代码 
#include<stdio.h>

int main()
{
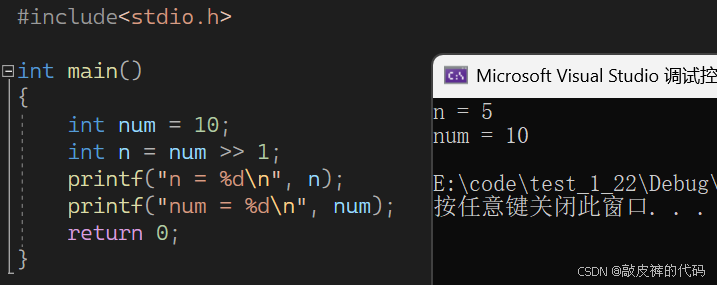
    int num = 10;
    int n = num >> 1;
    printf("n = %d\n", n);
    printf("num = %d\n", num);
    return 0;
}

运行结果：

警告⚠：对于移位运算符，不要移动负数位，这个是标准未定义的。

例如：

cpp 复制代码 
int num = 10;
num >> -1;    //error

5 位操作符：&、|、^、~

cpp 复制代码 
&    //按位与
|    //按位或
^    //按位异或
~    //按位取反

注：它们的操作数必须是整数！

5.1 位操作符详解

5.1.1 按位与 &

按位与 & 的计算规则：对应的二进制位进行与运算，只要有0就是0，两个同时为1才是1。

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 3;
    int b = -5;
    int c = a & b;

    //00000000000000000000000000000011 -- 3的补码
    //10000000000000000000000000000101 -- -5的原码
    //11111111111111111111111111111010 -- -5的反码
    //11111111111111111111111111111011 -- -5的补码
    //00000000000000000000000000000011 -- 3的补码
    //只要有0就是0，两个同时为1才是1，得出
    //00000000000000000000000000000011 -- 3的补码
    printf("c = %d\n", c);

    return 0;
}

输出结果：

5.1.2 按位或 |

按位或 | 的计算规则：对应的二进制位进行或运算，只要有1就是1，两个同时为0才是0。

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 3;
    int b = -5;
    int c = a | b;

    //00000000000000000000000000000011 -- 3的补码
    //10000000000000000000000000000101 -- -5的原码
    //11111111111111111111111111111010 -- -5的反码
    //11111111111111111111111111111011 -- -5的补码
    //00000000000000000000000000000011 -- 3的补码
    //只要有1就是1，两个同时为0才是0，得出
    //11111111111111111111111111111011 -- -5的补码
    printf("c = %d\n", c);

    return 0;
}

输出结果：

5.1.3 按位异或 ^

按位异或 ^ 的计算规则：对应的二进制位进行异或运算，相同就是0，相异就是1。

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 3;
    int b = -5;
    int c = a ^ b;

    //00000000000000000000000000000011 -- 3的补码
    //10000000000000000000000000000101 -- -5的原码
    //11111111111111111111111111111010 -- -5的反码
    //11111111111111111111111111111011 -- -5的补码
    //00000000000000000000000000000011 -- 3的补码
    //相同为0，相异为1，得出
    //11111111111111111111111111111000 -- 补码
    //10000000000000000000000000000111 -- 反码
    //10000000000000000000000000001000 -- 原码 -8
    printf("c = %d\n", c);

    return 0;
}

输出结果：

5.1.4 按位取反 ~

按位取反 ~ ，顾名思义就是把1变成0，把0变成1。

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 1;
    int b = ~a;

    //00000000000000000000000000000001 -- 1的补码
    //把0变成1，把1变成0，得到
    //11111111111111111111111111111110 -- 补码
    //10000000000000000000000000000001 -- 取反
    //10000000000000000000000000000010 -- +1  即
    //10000000000000000000000000000010 -- 原码 -2

    printf("%d\n", b);

    return 0;
}

输出结果：

5.2 一道变态的面试题

题目：不能创建临时变量（第三个变量），实现两个整数的交换。

5.2.1 方法1

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 3;
    int b = 5;
    printf("a = %d b = %d\n", a, b);
    //交换a和b的值
    a = a + b;
    b = a - b;
    a = a - b;
    
    printf("a = %d b = %d\n", a, b);
    return 0;
}

这种写法的缺陷是：a和b如果非常大，求和后的结果超过了整型的最大值，那么就出现问题了。

5.2.2 方法2

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 3;
    int b = 5;
    printf("a = %d b = %d\n", a, b);
    //交换a和b的值
    a = a ^ b;
    b = a ^ b;    
    a = a ^ b;
    
    printf("a = %d b = %d\n", a, b);
    return 0;
}

这里我们用到了异或操作符的特点：

  • a^a = 0
  • 0^a = a
cpp 复制代码 
a = a ^ b;
b = a ^ b;    //a^b^b = a
a = a ^ b;    //a^b^a = b
//这样就实现了交换

这种方法就算a和b非常大，也不会出现溢出的情况。但是在以后软件开发的过程中，一般会直接选用创建临时变量来交换值的办法，因为创建临时变量的代码可读性比较高，也比较容易想到，运行效率也比异或的办法高；异或的这种办法还只仅限于用在交换整数，如果换成交换浮点数就不行了。

5.3 练习1

练习1：编写代码实现：求一个整数存储在内存中的二进制中1的个数。

5.3.1 方法1

方法1：我们采用对这个整数不断 %2 和 /2 来求出存储在内存中的二进制中1的个数，因为我们从 2.1.1 中知道在10进制转2进制数字的时候就是对一个数除以二，得到一个余数，继续除以二，再得到一个余数，最后将余数从下往上排列就是该数字的二进制形式。

通过这个思路我们就可以得到如下代码：

cpp 复制代码 
#include<stdio.h>

int count_one_bit(int num)
{
    int count = 0;
    while (num)
    {
        if (num % 2 == 1)
        {
            count++;
        }
        num = num / 2;
    }
    return count;
}

int main()
{
    int num = 0;
    scanf("%d", &num);
    int n = count_one_bit(num);
    printf("%d\n", n);
    return 0;
}

思考一下：这段代码是否存在问题呢？
显然，这段代码虽然能够求一个正整数存储在内存中的二进制中1的个数，负整数是无法达到计算的目的的，如何改进呢？我们只需要把函数的形参类型改成无符号整型就可以了，假如我们输入 -1 ，-1的二进制在内存中存储的是11111111111111111111111111111111（补码），如果将它转换为无符号整数，那么它的最高位的符号位就变成了数值位，数值上它就变成了4294967295，再对这个数不断 %2 和 /2 也就可以求出该数存储在内存中的二进制中1的个数，从而达到求出负整数存储在内存中的二进制中1的个数。

改后代码：

cpp 复制代码 
#include<stdio.h>

int count_one_bit(unsigned int num)    //无符号整型
{
    int count = 0;
    while (num)
    {
        if (num % 2 == 1)
        {
            count++;
        }
        num = num / 2;
    }
    return count;
}

int main()
{
    int num = 0;
    scanf("%d", &num);
    int n = count_one_bit(num);
    printf("%d\n", n);
    return 0;
}

5.3.2 方法2

方法2：我们首先我们要知道：

  • 对任意一个数a按位与1，如果等于1，就说明a的二进制位中最低位是1
  • 对任意一个数a按位与1，如果等于0，就说明a的二进制位中最低位是0
cpp 复制代码 
int a = 15;
//00000000000000000000000000001111 -- 15的补码
//00000000000000000000000000000001 -- 1的补码
//对它们进行按位与操作，只要有0就是0，两个同时为1才是1
a & 1 == 1;
a & 1 == 0;

我们一直通过 &1 判断这个数的最低位是否为1，然后再对这个数 >>1 （右移1位），就可以判断最低位的上一位是否为1，判断最高位是否为1，只需要右移31位就可以了。在这段代码中，我们是对内存中存储的二进制位进行操作的，所以不需要考虑正负数的问题。

参考代码：

cpp 复制代码 
#include<stdio.h>

int count_one_bit(int a)
{
    int count = 0;
    int i = 0;
    for (i = 0; i < 32; i++)
    {
        if (((a >> i) & 1) == 1)    //右移i位，判断是否为1
        {
            count++;
        }
    }
    return count;
}

int main()
{
    int a = 0;
    scanf("%d", &a);
    int n = count_one_bit(a);
    printf("%d\n", n);
    return 0;
}

思考一下：还能不能更加优化？这里必须循环32次。接下来有请方法3！！

5.3.3 方法3

方法3：核心就是 n = n & (n-1) ，这个表达式可以把n的二进制中最右边的1去掉。这种办法比较难想到。

cpp 复制代码 
n = 15
1111 - n ①
1110 - n-1
n = n & (n - 1)
1110 - n ②
1101 - n-1
n = n & (n - 1)
1100 - n ③
1011 - n-1
n = n & (n - 1)
1000 - n ④
0111 - n-1
n = n & (n - 1)
0000 - n ⑤

所以我们可以看这个表达式执行几次之后n变成0了，那么n的二进制中就有几个1。

参考代码：

cpp 复制代码 
#include<stdio.h>

int count_one_bit(int n)
{
    int count = 0;
    while (n)
    {
        n = n & (n - 1);
        count++;
    }
    return count;
}

int main()
{
    int num = 0;
    scanf("%d", &num);
    int n = count_one_bit(num);
    printf("%d\n", n);
    return 0;
}
5.3.3.1 知识迁移

练习：判断一个数是否是2的次方数

cpp 复制代码 
000001 - 1  - 2的零次方
000010 - 2  - 2的一次方
000100 - 4  - 2的二次方
001000 - 8  - 2的三次方
010000 - 16 - 2的四次方
100000 - 32 - 2的五次方
...

由此我们不难发现，2的次方数的2进制序列里面只有一个位是1，那我们就看可以利用方法3中的表达式来实现判断。

参考代码：

cpp 复制代码 
#include<stdio.h>

int main()
{
    int n = 0;
    scanf("%d", &n);
    if ((n & (n - 1)) == 0)
    {
        printf("Yes\n");
    }
    else
    {
        printf("No\n");
    }
    return 0;
}

5.4 练习2

练习2：二进制位置0或者置1

编写代码将13二进制序列的第5位修改为1，然后再改回0

cpp 复制代码 
13的2进制序列： 00000000000000000000000000001101
将第5位置为1后：00000000000000000000000000011101
将第5位再置为0：00000000000000000000000000001101

参考代码：

cpp 复制代码 
#include<stdio.h>

int main()
{
    int a = 13;
    a = a | (1<<4);
    printf("a = %d\n", a);
    a = a & ~(1<<4);
    printf("a = %d\n", a);
    return 0;
}

6 单目操作符

单目操作符有这些：! 、++ 、-- 、& 、* 、+ 、- 、~ 、sizeof 、(类型)

单目操作符的特点是只有一个操作数，在单目操作符中只有 & 和 * 没有介绍，这两个操作符，我们放在指针部分介绍。

《C语言》数据类型和变量_16位有符号数65530是负多少-CSDN博客

7 逗号表达式

cpp 复制代码 
exp1, exp2, exp3, ...expN

逗号表达式，就是用都要隔开的多个表达式。

逗号表达式，从左向右依次执行。整个表达式的结果是最后一个表达式的结果。

cpp 复制代码 
//代码1
int a = 1;
int b = 2;
int c = (a > b, a = b + 2, a, b = a + 1);    //逗号表达式
//c是多少？
//答案是13

//代码2
if(a = b + 1, c = a / 2, d > 0)
//if判断条件是d>0，前面的表达式并不改变d的值，但还是要运算
//假如c=a/2改成d=a/2就会影响判断条件了

//代码3
a = get_val();
count_val(a);
while(a > 0)
{
    //...
    a = get_val();
    count_val(a);
}

//如果用都好表达式，可以改写成：
while(a = get_val(), count_val(a), a > 0)
{
    //...
}

8 下标访问 、函数调用( )

8.1 下标引用操作符

操作数：一个数组名 + 一个索引值（下标）

cpp 复制代码 
int arr[10];    //创建数组
arr[9] = 10;    //使用下标操作符

的两个操作数是arr和9。

8.2 函数调用操作符

接受一个或者多个操作数：第一个操作数是函数名，剩余的操作数就是传递给函数的参数。所以函数调用操作符至少有一个操作数（函数名）。

cpp 复制代码 
#include<stdio.h>

int Add(int x, int y)
{
    return x + y;
}

int main()
{
    int x = 0;
    int y = 0;
    scanf("%d%d", &x, &y);    //()函数调用操作符
    int z = Add(x, y);    //()函数调用操作符
    printf("%d\n", z);    //()函数调用操作符
    return 0;
}

9 结构成员访问操作符

9.1 结构体

C语言已经提供了内置类型，如：char、short、int、long、float、double等，但是只有这些内置类型还是不够的，假设我们想描述一个学生，描述一本书，这时单一的内置类型是不行的。描述一个学生需要名字、年龄、学号、身高、体重等；描述一本书需要作者、出版社、定价等。C语言为了解决这个问题，增加了结构体这种自定义的数据类型，让程序员可以自己创造适合的类型。

结构是一些值的集合，这些值称为成员变量。结构的每个成员可以是不同类型的变量，如：标量、数组、指针，甚至是其他结构体。

9.1.1 结构的声明

cpp 复制代码 
struct tag
{
    member-list;
}variable-list;
  • tag：结构体的标签名，自己命名，大致用于描述什么。
  • member-list：成员列表，可以有1个或者多个成员。
  • variable-list：变量列表。

描述一个学生：

cpp 复制代码 
struct Stu
{
    char name[20];    //名字
    int age;    //年龄
    float score;    //成绩
};    //分号不能丢

9.1.2 结构体变量的定义和初始化

cpp 复制代码 
//代码1：变量的定义
struct Point
{
    int x;
    int y;
}p1;    //声明类型的同时定义变量p1（全局变量）

struct Point p2;    //定义结构体变量p2

//代码2：初始化
struct Point p3 = {10, 20};

struct Stu    //类型声明
{
    char name[20];    //名字
    int age;    //年龄
    float score;    //成绩
};

struct Stu s1 = {"PIKU", 20, 100.0f};    //初始化
struct Stu s2 = {.score=95.5f, .name="SHUBAO", .age=21};    //指定顺序初始化

//代码3
struct Data
{
    int num;
    struct Point p;
}d1 = {10, {15, 25}};    //结构体嵌套初始化

struct Data d2 = {25, {30, 52}};    //结构体嵌套初始化

9.2 结构成员访问操作符

9.2.1 结构体成员的直接访问

结构体成员的直接访问是通过点操作符（.）访问的。点操作符接受两个操作数。如下所示：

cpp 复制代码 
#include<stdio.h>

struct Point
{
    int x;
    int y;
};

struct Data
{
    int num;
    struct Point p;
}d = {10, {15, 25}};

int main()
{
    printf("num = %d x = %d y = %d\n", d.num, d.p.x, d.p.y);
    return 0;
}

使用方式：结构体变量.成员名

9.2.2 结构体成员的间接访问

有时候我们得到的不是一个结构体变量，而是得到了一个指向结构体的指针。如下所示：

cpp 复制代码 
#include<stdio.h>

struct Point
{
    int x;
    int y;
};

int main()
{
    struct Point p = {3, 4};
    struct Point *ps = &p;
    ps->x = 10;
    ps->y = 20;
    printf("x = %d y = %d\n", ps->x, ps->y);
    return 0;
}

使用方式：结构体指针->成员名

综合举例：

cpp 复制代码 
#include<stdio.h>
#include<string.h>

struct Stu
{
    char name[20];    //名字
    int age;    //年龄
    float score;    //成绩
};

void print_stu(struct Stu s)
{
    printf("%s %d %lf\n", s.name, s.age, s.score);
}

void set_stu(struct Stu* ps)
{
    strcpy(ps->name, "皮裤");
    ps->age = 20;
    ps->score = 100.0f;
}

int main()
{
    struct Stu s = { "书包", 21, 95.5f };
    print_stu(s);
    set_stu(&s);
    print_stu(s);
    return 0;
}

更多关于结构体的知识，会在后面的《C语言》自定义类型：结构体中介绍。

10 操作符的属性：优先级、结合性

C语言的操作符有2个重要的属性：优先级、结合性，这两个属性决定了表达式求值的计算顺序。

10.1 优先级

优先级指的是，如果一个表达式包含多个运算符，哪个运算符应该优先执行。各种运算符的优先级是不一样的。

cpp 复制代码 
3 + 4 * 5;

上面示例中，表达式 3 + 4 * 5 里面既有加法运算符（ + ），又有乘法运算符（ * ）。由于乘法的优先级高于加法，所以会先计算 4 * 5 ，而不是先计算3 + 4 。

10.2 结合性

如果两个运算符优先级相同，优先级没办法确定先计算哪个了，这时候就看结合性了，则根据运算符是左结合，还是右结合，决定运行顺序。大部分运算符是左结合（从左到右执行），少数运算符是右结合（从右到左执行），比如赋值操作符（ =）。

cpp 复制代码 
5 * 6 / 2;

上面示例中， * 和 / 的优先级相同，它们都是左结合运算符，所以从左到右执行，先计算 5 * 6 ，再计算6 / 2 。

运算符的优先级顺序很多，下面是部分运算符的优先级顺序（按照优先级从高到低排列），建议大概记住这些操作符的优先级就行，其他操作符在使用的时候查看下面表格就可以了。

  • 圆括号（ ( ) ）
  • 自增运算符（ ++ ），自减运算符（ -- ）
  • 单目操作符（ + 和 - ）
  • 乘法（ * ），除法（ / ）
  • 加法（ + ），减法（ -）
  • 关系运算符（ < 、**>**等）
  • 赋值运算符（ = ）

由于圆括号的优先级最高，可以使用它改变其他运算符的优先级。

参考：https://en.cppreference.com/w/c/language/operator_precedence

11 表达式求值

11.1 整型提升

C语言整型算术运算总是至少以缺省整型类型的精度来进行的。

为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

整型提升的意义：表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器（ALU）的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。

因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。

通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

cpp 复制代码 
char a, b, c;
...
a = b + c;

b和c的值被提升为普通整型，然后再执行加法运算。

加法运算完成之后，结果将被截断，然后再存储于a中。

如何进行整型提升能？

  1. 有符号整数提升是按照变量的数据类型的符号位来提升的
  2. 无符号整数提升，高位补0
cpp 复制代码 
//负数的整型提升
char c1 = -1;
变量c1的二进制位（补码）中只有8个比特位：
11111111
因为 char 为有符号的 char
所以整型提升的时候，高位补充符号位，即为1
提升之后的结果是：
11111111111111111111111111111111

//正数的整型提升
char c2 = 1;
变量c2的二进制位（补码）中只有8个比特位：
00000001
因为 char 为有符号的 char
所以整型提升的时候，高位补充符号位，即为0
提升后的结果是：
00000000000000000000000000000001

//无符号整型提升，高位补0

举例来说：

cpp 复制代码 
#include<stdio.h>

int main()
{
    //char类型的取值范围是-128-127
    //char是占用1个字节的，1个字节是8个bit位
    char c1 = 125;
    //00000000000000000000000001111101
    //发生截断
    //01111101 - c1
    //
    char c2 = 10;
    //00000000000000000000000000001010
    //发生截断
    //00001010 - c2
    //
    char c3 = c1 + c2;
    //00000000000000000000000001111101 - c1 - 有符号的char整型提升，高位补0
    //00000000000000000000000000001010 - c2 - 有符号的char整型提升，高位补0
    //00000000000000000000000010000111 - 计算结果
    //发生截断
    //10000111 - c3
    //有符号的char整型提升，高位补1
    //11111111111111111111111110000111 - 补码
    //10000000000000000000000001111000 - 反码
    //10000000000000000000000001111001 - 原码
    //-121
    printf("%d\n", c3);         //-121
    printf("%d\n", c1 + c2);    //135
    //c1 + c2
    //00000000000000000000000001111101 - c1 - 有符号的char整型提升，高位补0
    //00000000000000000000000000001010 - c2 - 有符号的char整型提升，高位补0
    //00000000000000000000000010000111 - 计算结果
    //计算结果并没有放到char类型里面去，就不会发生截断，所以c1 + c2直接打印的结果为135
    //
    //%d是打印有符号的正数
    return 0;
}

运行结果：

11.2 算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

cpp 复制代码 
long double            ^
double                 |
float                  |
unsigned long int      |
long int               |
unsigned int           |
int                    |

如果某个操作数的类型在上面这个列表中排名靠后，那么首先要转换为另外一个操作数的类型后执行运算。

cpp 复制代码 
int + float -- int -> float
float + double -- float -> double

11.3 问题表达式解析

11.3.1 表达式1

cpp 复制代码 
//表达式的求值部分由操作符的优先级决定。
//表达式1
a * b + c * d + e * f

表达式1在计算的时候，由于***** 比 + 的优先级高，只能保证，* 的计算是比**+** 早，但是优先级并不能决定第三个***** 比第一个 **+**早执行。

所以表达式的计算机顺序就可能是：

cpp 复制代码 
a * b
c * d
a * b + c * d
e * f
a * b + c * d + e * f

或者：

cpp 复制代码 
a * b
c * d
e * f

a * b + c * d
a * b + c * d + e * f

11.3.2 表达式2

cpp 复制代码 
//表达式2
c + --c;

同上，操作符的优先级只能决定自减 -- 的运算在 + 的运算的前面，但是外卖并没有办法得知，+ 操作符的左操作数的获取在右操作数之前还是之后求值，所以结果是不可测的，是有歧义的。

11.3.3 表达式3

cpp 复制代码 
//表达式3
#include<stdio.h>
int main()
{
    int i = 10;
    i = i-- - --i * ( i = -3 ) * i++ + ++i;
    printf("i = %d\n", i);
    return 0;
}

表达式3在不同编译器中测试结果：非法表达式程序的结果

11.3.4 表达式4

cpp 复制代码 
#include<stdio.h>

int fun()
{
    static int count = 1;
    return ++count;
}

int main()
{
    int answer;
    answer = fun() - fun() * fun();
    printf("%d\n", answer);
    return 0;
}

这个代码有没有实际的问题？有问题！！

虽然在大多数的编译器上求得结果都是相同的。

但是上述代码 answer = fun() - fun() * fun(); 中我们只能通过操作符的优先级得知：先算乘法，再算减法。

函数的调用先后顺序是无法通过操作符的优先级决定的。

11.3.5 表达式5

cpp 复制代码 
//表达式5
#include<stdio.h>

int main()
{
    int i = 1;
    int ret = (++i) + (++i) + (++i);
    printf("%d\n", ret);
    printf("%d\n", i);
    return 0;
}
//看看不同编译器下的结果

gcc编译器执行结果：

cpp 复制代码 
10
4

VS2022运行结果：

cpp 复制代码 
12
4

看看同样的代码产生了不同的记过，这是为什么？

简单看一下汇编代码就可以分析清楚，这段代码中的第一个 + 在执行的时候，第三个 ++ 是否执行，这个是不确定的，因为依靠操作符的优先级和结合性是无法决定第一个 + 和第三个前置 **++**的先后顺序。

11.4 总结

即使有了操作符的优先级和结合性，我们写出的表达式依然有可能不能通过操作符的属性确定唯一的计算路径，那这个表达式就是存在潜在风险的，建议不要写出特别复杂的表达式。

相关推荐
Hello:CodeWorld21 小时前
C 风格变参 vs C++ 变参模板：核心区别与选型指南
c语言·c++·算法
十月的皮皮1 天前
C语言学习笔记20260606- 求月份天数三种写法
c语言·笔记·学习
caimouse1 天前
Reactos 第 5 章 进程与线程 — 5.8 Windows 的 APC 机制
c语言·windows
努力攻坚操作系统1 天前
编程语言编译运行机制对比：C / Java / Python
java·c语言·python
学会去珍惜1 天前
C语言简介
c语言·开发语言
凡人叶枫1 天前
Effective C++ 条款07：为多态基类声明 virtual 析构函数
linux·c语言·开发语言·c++
matlabgoodboy1 天前
计算机java程序代写python代码编写c/c++代做qt设计php开发matlab
java·c语言·python
caimouse1 天前
Reactos 第 5 章 进程与线程 — 5.11 线程本地存储 TLS
c语言·windows
格发许可优化管理系统1 天前
Mentor许可证使用规定全解析
java·大数据·c语言·开发语言·c++
caimouse1 天前
Reactos 第 5 章 进程与线程 — 5.12 进程挂靠
c语言·windows
热门推荐
01《置身钉内》原文-可播放阅读02【AI】2026 年具身智能模型和世界模型总结03GitHub 镜像站点04Claude Code、Codex、Cursor三分天下：2026年AI编程Agent生态全景剖析052026 AI 编程工具终极实战指南：Cursor vs Claude Code vs Copilot，开发者该怎么选？06Codex 下载安装指南：Windows 和 macOS 官方版下载072026 年 AI 编程工具终极横评：Cursor vs Claude Code vs Copilot vs Windsurf08AI科技热点日报 | 2026年6月1日09【踩坑记录 | 第一篇】微软商店无法使用时，如何手动安装 OpenAI Codex？附`.msix`文件系统错误解决方法10CC-Switch 下载、安装与使用配置指南【2026.5.29】