朴素贝叶斯算法
利用概率值进行分类的一种机器学习算法
什么是概率? 一件事情发生的可能性,取值在【0,1】之间。
比如:抛硬币正面向上的概率、6面骰子抛出5这一面的概率
• 例子: 判断女神对你的喜欢情况
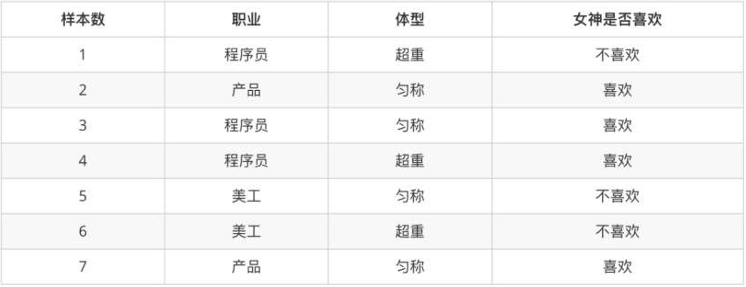
**• 条件概率:**表示事件A在另外一个事件B已经发生条件下的发生概率,P(A|B)
• 比如:在女神喜欢的条件下,职业是程序员的概率?
• 女神喜欢条件下,有 2、3、4、7 共 4 个样本
• 4 个样本中,有程序员 3、4 共 2 个样本
• 则 P(程序员|喜欢) = 2/4 = 0.5
• 联合概率: 表示多个条件同时成立的概率,P(AB) = P(A) * P(B|A) = P(B)* P(A|B)
• 比如:职业是程序员并且体型匀称的概率?
• 数据集中,共有 7 个样本
• 职业是程序员有 1、3、4 共 3 个样本,则其概率为:3/7
• 在职业是程序员,体型是匀称的有样本3,共 1 个样本,则其概率为:1/3
• 则即是程序员又体型匀称的概率为:3/7 * 1/3 = 1/7
• 联合概率 + 条件概率
• 比如:在女神喜欢的条件下,职业是程序员、并且超重的概率? P(程序员, 超重|喜欢)
• 在女神喜欢的条件下,有 2、3、4、7 共 4 个样本
• 在这 4 个样本中,职业是程序员有 3、4 共 2 个样本,则其概率为:2/4=0.5
• 在这 2 个样本中,体型超重的有样本4,共 1 个样本,则其概率为:1/2 = 0.5
• 则 P(程序员, 超重|喜欢) = 0.5 * 0.5 = 0.25
**• 相互独立:**如果P(A, B) = P(A)P(B),则称事件A与事件B相互独立
• 比如:女神喜欢程序员的概率,女神喜欢产品经理的概率,两个事件没有关系
• 简言之
• 条件概率:在去掉部分样本的情况下,计算某些样本的出现的概率,表示为:P(B|A)
• 联合概率:多个事件同时发生的概率是多少,表示为:P(AB) = P(B)*P(A|B)
• 贝叶斯公式
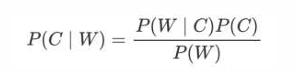
• P(C) 表示 C 出现的概率,一般是目标值
• P(W | C) 表示 C 条件 W 出现的概率
• P(W) 表示 W 出现的概率

-
P(C | W) = P(喜欢 | (程序员,超重))
-
P(W | C) = P((程序员,超重) | 喜欢)
-
P(C) = P(喜欢)
-
P(W) = P(程序员,超重)
1.根据训练样本估计先验概率P(C): P(C) = P(喜欢) = 4/7
2.根据条件概率P(W | C)调整先验概率:
3.此时我们的后验概率P(W | C) * P(C)为: P(W | C) = P((程序员,超重) | 喜欢) = 1/4 P(W | C) * P(C) = P((程序员,超重) | 喜欢) * P(喜欢) = 4/7 * 1/4 = 1/7
4.那么该部分数据占所有既为程序员,又超重的人中的比例是多少呢? P(W) = P(程序员,超重) = P(程序员) * P(超重 | 程序员) = 3/7 * 2/3 = 2/7

朴素贝叶斯在贝叶斯基础上增加:特征条件独立假设,即:特征之间是互为独立的。 此时,联合概率的计算即可简化为:
-
P(程序员,超重|喜欢) = P(程序员|喜欢) * P(超重|喜欢)
-
P(程序员,超重) = P(程序员) * P(超重)
拉普拉斯平滑系数
为了避免概率值为 0,我们在分子和分母分别加上一个数值,这就是拉普拉斯平滑系数的作用

数学计算流程
1. 问题设定
训练数据(5封邮件)
| 邮件内容 | 类别 |
|---|---|
| "buy cheap viagra" | 垃圾邮件 |
| "cheap goods cheap" | 垃圾邮件 |
| "viagra deal" | 垃圾邮件 |
| "hello world" | 正常邮件 |
| "hello buy" | 正常邮件 |
测试邮件
"cheap viagra"2. 构建词汇表
从训练数据中提取所有不重复的单词,得到词汇表(共7个词):
{buy, cheap, viagra, goods, deal, hello, world}3. 计算先验概率
-
垃圾邮件数:3
-
正常邮件数:2
-
总邮件数:5
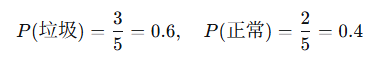
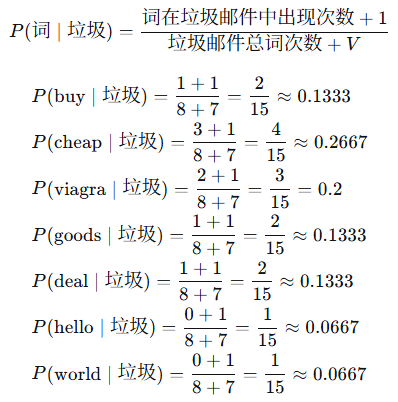
4. 计算似然概率(使用拉普拉斯平滑)
4.1 统计垃圾邮件中的词频
-
垃圾邮件包含的邮件内容及词频:
-
邮件1: "buy cheap viagra" → buy(1), cheap(1), viagra(1)
-
邮件2: "cheap goods cheap" → cheap(2), goods(1)
-
邮件3: "viagra deal" → viagra(1), deal(1)
-
-
垃圾邮件总词次数(重复计数):3 + 3 + 2 = 8
-
词汇表大小 V=7
使用拉普拉斯平滑(加1平滑)计算每个词在垃圾邮件中的条件概率:
4.2 统计正常邮件中的词频
-
正常邮件包含的邮件内容及词频:
-
邮件4: "hello world" → hello(1), world(1)
-
邮件5: "hello buy" → hello(1), buy(1)
-
-
正常邮件总词次数:2 + 2 = 4
-
词汇表大小 V=7
计算每个词在正常邮件中的条件概率:
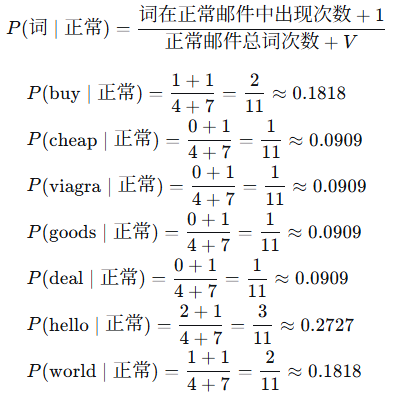
5. 对新邮件进行分类
5.1 提取测试邮件特征
测试邮件:"cheap viagra"
出现的词:{cheap, viagra}(忽略未出现的词)
5.2 计算后验概率(分子部分)
朴素贝叶斯公式(多项式模型):

- 垃圾邮件类别:

- 正常邮件类别:

5.3 比较并归一化
-
垃圾邮件得分:0.032
-
正常邮件得分:0.003306
归一化(得到概率):

6. 分类结果
由于 P(垃圾∣邮件)>P(正常∣邮件)P(垃圾∣邮件)>P(正常∣邮件),该邮件被分类为垃圾邮件。
关键点总结
-
先验概率:基于训练数据中各类别的比例。
-
似然概率:使用拉普拉斯平滑避免零概率问题。
-
条件独立假设:邮件中每个词的出现概率相互独立。
-
多项式模型:考虑词的出现次数(本例中测试邮件每个词出现一次)。
-
取对数技巧:实际应用中常对概率取对数,将连乘转为连加,防止下溢。
例商品评论情感分析:
需求 已知商品评论数据,根据数据进行情感分类(好评、差评)
商品评论情感分析流程
1 获取数据
2 数据基本处理
2-1 处理数据y
2-2 加载停用词
2-3 处理数据x 把文档分词
2-4 统计词频矩阵 作为句子特征
2-5 准备训练集测试集
3 模型训练
4-1 实例化贝叶斯 添加拉普拉斯平滑参数
4 模型预测
5 模型评估
代码
python
# 1.导入依赖包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import jieba
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
def dm01():
# 2.获取数据
data_df = pd.read_csv('./data/数据评价.csv', encoding='gbk')
print('data_df --> ', data_df)
# 3.数据基本处理
# 3-1 处理数据y
data_df['评论标号'] = np.where(data_df['评价'] == '好评', 1, 0)
y = data_df['评论标号']
print('data_df -->\n', data_df)
# 3-2 加载停用词
stopwords = []
with open('./data/stopwords.txt', 'r', encoding='utf-8') as f:
lines = f.readlines()
stopwords = [line.strip() for line in lines]
stopwords = list(set(stopwords)) # 去重
print(stopwords[:5])
# 3-3 处理数据x 把文档分词
comment_list = [','.join(jieba.lcut(line)) for line in data_df['内容']]
# print('comment_list-->\n', comment_list)
# 3-4 统计词频矩阵 作为句子特征
transfer = CountVectorizer(stop_words=stopwords)
x = transfer.fit_transform(comment_list)
mynames = transfer.get_feature_names_out()
x = x.toarray()
# 3-5 准备训练集测试集
x_train = x[:10, :] # 准备训练集
y_train = y.values[0:10]
x_test = x[10:, :] # 准备测试集
y_test = y.values[10:]
print('x_train.shape-->', x_train.shape)
print('y_train.shape-->', y_train.shape)
# 4.模型训练
# 4-1 实例化贝叶斯 # 添加拉普拉修正平滑参数
mymultinomialnb = MultinomialNB()
mymultinomialnb.fit(x_train, y_train)
# 5.模型预测
y_pred = mymultinomialnb.predict(x_test)
print('预测值-->', y_pred)
print('真实值-->', y_test)
# 6.模型评估
myscore = mymultinomialnb.score(x_test, y_test)
print('myscore-->', myscore)
dm01()执行结果
python
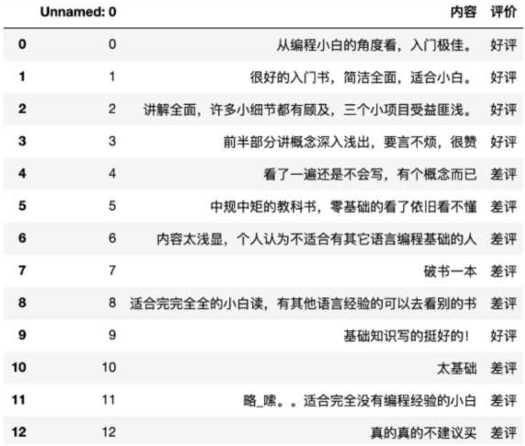
data_df --> Unnamed: 0 内容 评价
0 0 从编程小白的角度看,入门极佳。 好评
1 1 很好的入门书,简洁全面,适合小白。 好评
2 2 讲解全面,许多小细节都有顾及,三个小项目受益匪浅。 好评
3 3 前半部分讲概念深入浅出,要言不烦,很赞 好评
4 4 看了一遍还是不会写,有个概念而已 差评
5 5 中规中矩的教科书,零基础的看了依旧看不懂 差评
6 6 内容太浅显,个人认为不适合有其它语言编程基础的人 差评
7 7 破书一本 差评
8 8 适合完完全全的小白读,有其他语言经验的可以去看别的书 差评
9 9 基础知识写的挺好的! 好评
10 10 太基础 差评
11 11 略_嗦。。适合完全没有编程经验的小白 差评
12 12 真的真的不建议买 差评
data_df -->
Unnamed: 0 内容 评价 评论标号
0 0 从编程小白的角度看,入门极佳。 好评 1
1 1 很好的入门书,简洁全面,适合小白。 好评 1
2 2 讲解全面,许多小细节都有顾及,三个小项目受益匪浅。 好评 1
3 3 前半部分讲概念深入浅出,要言不烦,很赞 好评 1
4 4 看了一遍还是不会写,有个概念而已 差评 0
5 5 中规中矩的教科书,零基础的看了依旧看不懂 差评 0
6 6 内容太浅显,个人认为不适合有其它语言编程基础的人 差评 0
7 7 破书一本 差评 0
8 8 适合完完全全的小白读,有其他语言经验的可以去看别的书 差评 0
9 9 基础知识写的挺好的! 好评 1
10 10 太基础 差评 0
11 11 略_嗦。。适合完全没有编程经验的小白 差评 0
12 12 真的真的不建议买 差评 0
['', '这会儿', '本', '为什麽', '当着']
Building prefix dict from the default dictionary ...
Loading model from cache C:\Users\ADMINI~1\AppData\Local\Temp\jieba.cache
Loading model cost 0.686 seconds.
Prefix dict has been built successfully.
x_train.shape--> (10, 37)
y_train.shape--> (10,)
预测值--> [0 0 0]
真实值--> [0 0 0]
myscore--> 1.0