寒假集训1——暴力和枚举

1.P1047 [NOIP 2005 普及组] 校门外的树

题目描述

某校大门外长度为 l 的马路上有一排树，每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴，马路的一端在数轴 0 的位置，另一端在 l 的位置；数轴上的每个整数点，即 0,1,2,...,l，都种有一棵树。

由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的树（包括区域端点处的两棵树）移走。你的任务是计算将这些树都移走后，马路上还有多少棵树。

输入格式

第一行有两个整数，分别表示马路的长度 l 和区域的数目 m。

接下来 m 行，每行两个整数 u,v，表示一个区域的起始点和终止点的坐标。

输出格式

输出一行一个整数，表示将这些树都移走后，马路上剩余的树木数量。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

说明/提示

【数据范围】

对于 20% 的数据，保证区域之间没有重合的部分。
对于 100% 的数据，保证 1≤l≤104，1≤m≤100，0≤u≤v≤l。

【题目来源】

NOIP 2005 普及组第二题

由题目观察就得到差分数组的第一项是一，后面都是零。

有一个要注意的：从0号开始种树。

cpp 复制代码

#include<iostream>
using namespace std;
const int N=1e4+10;
typedef long long LL;
LL f[N];//前缀和数组
LL len,m,l,r;
int main()
{
    f[1]=1;
    cin>>len>>m;
    len++;
    int d=-1;
    while(m--)
    {
        cin>>l>>r;
        l++;
        r++;
        f[l]+=d;
        f[r+1]-=d;
    }
    for(int i=1;i<=len;i++)
        f[i]+=f[i-1];
    int cnt=0;
    for(int i=1;i<=len;i++)
    {
        if(f[i]>0)
            cnt++;
    }
    cout<<cnt<<endl;
    return 0;
}

2.枚举 · 例7-【模板】差分

略。

3.P1003 [NOIP 2011 提高组] 铺地毯

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n 张地毯，编号从 1 到 n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 n+2 行。

第一行，一个整数 n，表示总共有 n 张地毯。

接下来的 n 行中，第 i+1 行表示编号 i 的地毯的信息，包含四个整数 a,b,g,k，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 (a,b) 以及地毯在 x 轴和 y 轴方向的长度。

第 n+2 行包含两个整数 x 和 y，表示所求的地面的点的坐标 (x,y)。

输出格式

输出共 1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

输入 #2复制

复制代码

输出 #2复制

复制代码

-1

说明/提示

【样例解释 1】

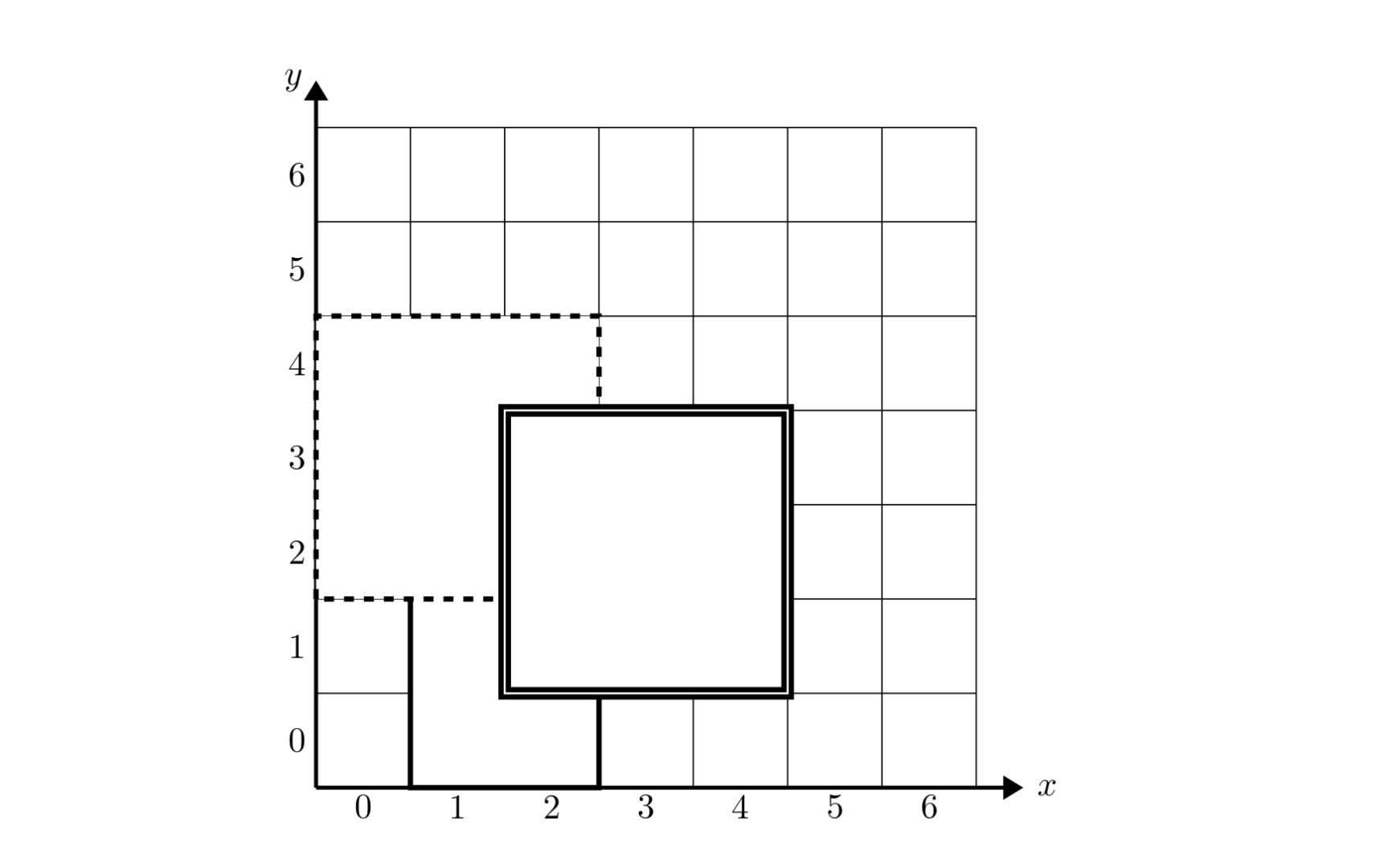
如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点 (2,2) 的最上面一张地毯是 3 号地毯。

【数据范围】

对于 30% 的数据，有 n≤2。

对于 50% 的数据，0≤a,b,g,k≤100。

对于 100% 的数据，有 0≤n≤104, 0≤a,b,g,k≤105。

noip2011 提高组 day1 第 1 题。

cpp 复制代码

#include<iostream>
typedef long long LL;
const int N=1e4+10;
LL a[N],b[N],g[N],k[N],n;
LL x,y;
using namespace std;
int solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i]>>b[i]>>g[i]>>k[i];
    cin>>x>>y;
    for(int i=n;i>=1;i--)
    {
        if(x>=a[i] && x<=a[i]+g[i]
          && y>=b[i] && y<=b[i]+k[i])
            return i;
    }
    return -1;
}
int main()
{
    LL ret=solve();
    cout<<ret<<endl;
    return 0;
}

4.P1014 [NOIP 1999 普及组] Cantor 表

题目描述

现代数学的著名证明之一是 Georg Cantor 证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的：

我们以 Z 字形给上表的每一项编号。第一项是 1/1，然后是 1/2，2/1，3/1，2/2，...

输入格式

整数 N（1≤N≤107）。

输出格式

表中的第 N 项。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

1/4

说明/提示

2024-11-18 0:30 数据中加入了样例，放在不计分的子任务 2 中。

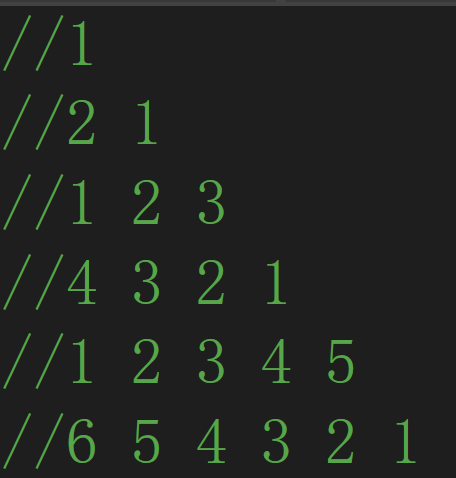
这一题就是观察规律，分别计算出行和列。我是观察的分母，发现分母存在上图的规律。有了分母之后，能发现在一行里面，分母跟分子相加得到的是特定的数，这个数就是行数加一，从而能算出分子。如果行是偶数的话，就会反着，最后要交换一下。

cpp 复制代码

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int an;
    cin >> an;
    int row, col;
    row = sqrt(an * 2);
    if (row*(row+1)/2<an)
        row++;
    int last = row * (row + 1) / 2;
    col = row - (last - an);
    int mom = col;
    int son = row - col + 1;
   
    if (row % 2 == 0)
    {
        int tmp = mom;
        mom = son;
        son = tmp;
    }
    cout << son << "/" << mom << endl;
    return 0;
}

5.P3650 [USACO1.3] 滑雪课程设计Ski Course Design

题目描述

农民约翰的农场里有 n 座山峰，每座山都有一个在 0 到 100 之间的整数的海拔高度。在冬天,因为山上有丰富的积雪，约翰经常开办滑雪训练营。

不幸的是，约翰刚刚得知税法在滑雪训练营方面有新变化，明年开始实施。在仔细阅读法律后，他发现如果滑雪训练营的最高和最低的山峰海拔高度差大于 17 就要收税。因此，如果他改变山峰的高度（使最高与最低的山峰海拔高度差不超过 17 ），约翰可以避免支付税收。

如果改变一座山 x 单位的高度成本是 x2 单位，约翰最少需要付多少钱才能使海拔最高的山峰与海拔最低的山峰的高度之差不超过 17。约翰只愿意改变整数单位的高度。

输入格式

输入的第一行是一个整数，代表山峰的数量 n。

第 2 行到(n+1) 行，每行一个整数。第 i 行的整数 ai 代表第 i 座山的海拔高度。

输出格式

输出一行一个整数，代表约翰需要支付修改山海拔高度的总金额。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

说明/提示

样例输入输出 1 解释

约翰保持高度为 4、20 和 21 的山的高度。他增高高度为 1 的山，变成高度 4 ，花费 32=9。他降低了高度为 24 的山变成高度 21，也花费 32=9。因此总共花费 9+9=18。

数据规模与约定

对于 100% 的数据，1≤n≤1000，0≤ai≤100。

这一题我就是枚举的所有可能的最低点，再计算以这个点为最低点所需要的花费。因为以这个点为最低点的话，它就会有一个最低点最高点，如果超出了最低点最高点，然后就要加上花费。然后计算好之后就求最小的，输出最小的花费就行。

cpp 复制代码

#include<iostream>
using namespace std;
int h[10010];
int calc(int low, int h[], int n)
{
	int sum = 0;
	int high = low + 17;
	for (int i = 1;i <= n;i++)
	{
		if (h[i] < low)
			sum += (low - h[i]) * (low - h[i]);
		if (h[i] > high)
			sum += (h[i] - high) * (h[i] - high);
	}
	return sum;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 1;i <= n;i++)
		cin >> h[i];
	int min_cost = calc(1, h, n);
	for (int low = 2;low <= 73;low++)
		min_cost = min(min_cost, calc(low, h, n));
	cout << min_cost << endl;
	return 0;
}

6.P1618 三连击（升级版）

题目描述

将 1,2,...,9 共 9 个数分成三组，分别组成三个三位数，且使这三个三位数的比例是 A:B:C，试求出所有满足条件的三个三位数，若无解，输出 No!!!。

//感谢黄小U饮品完善题意

输入格式

三个数，A,B,C。

输出格式

若干行，每行 3 个数字。按照每行第一个数字升序排列。

输入输出样例

输入 #1复制

复制代码

1 2 3

输出 #1复制

复制代码

192 384 576
219 438 657
273 546 819
327 654 981

说明/提示

保证 0≤A<B<C≤999。

upd 2022.8.3：新增加二组 Hack 数据。

这一题其实一开始我也是没有过几个测试点，主要就是a等于零或者i不能被a整除，还有排除j和k超出范围的情况，也就是我注释那两行我没有考虑到。我开了一个st数组来表示状态，分别把i、j、k的个位、十位、百位都累计进去。

cpp 复制代码

#include<iostream>
using namespace std;
//累计i、j、k的个位、十位、百位
bool check(int a,int b,int c,int i,int j,int k)
{
    int st[10]={0,0,0,0,0,0,0,0,0,0};
    st[i/100]++;
    st[j/100]++;
    st[k/100]++;
    st[i/10%10]++;
    st[j/10%10]++;
    st[k/10%10]++;
    st[i%10]++;
    st[j%10]++;
    st[k%10]++;
    if(st[0]!=0)
        return false;
    for(int i=1;i<=9;i++)
    {
        if(st[i]!=1)
            return false;
    }
    return true;
}
int main()
{
    int a,b,c;
    int flag=0;
    cin>>a>>b>>c;
    for(int i=100;i<1000;i++)
    {
        //无解的情况：a=0或者i不能被a整除
        if(a==0 || (i%a!=0))
            continue;
        int j=i/a*b;
        int k=i/a*c;
        //排除j和k超出范围的情况
        if(j<100 || k<100 ||
           j>=1000||k>=1000)
            continue;
        if(check(a,b,c,i,j,k))
        {
            flag=1;
            cout<<i<<" "<<j<<" "<<k<<endl;
        }
    }
    if(flag==0)
        cout<<"No!!!"<<endl;
    return 0;
}