关键词:
Supervised Learning监督学习
Linear regression with one variable 一元线性回归
h(hypothesis) 假设
cost function 代价函数
squared error function 平方误差函数
Gradient descent 梯度下降
learning rate学习率
derivative导数项
目录
[2.1 Model representation](#2.1 Model representation)
[Housing Prices(Portland, OR) 房价预测](#Housing Prices(Portland, OR) 房价预测)
[Training set of housing prices (Portland, OR)训练集](#Training set of housing prices (Portland, OR)训练集)
[How do we represent h?](#How do we represent h?)
[2.2 Cost function 代价函数](#2.2 Cost function 代价函数)
[2.3 Cost function intuition I](#2.3 Cost function intuition I)
[2.4 Cost function intuition II](#2.4 Cost function intuition II)
[2.5 Gradient descent梯度下降](#2.5 Gradient descent梯度下降)
[2.6 Gradient descent intuition](#2.6 Gradient descent intuition)
[2.7 Gradient descent for linear regression梯度下降的线性回归](#2.7 Gradient descent for linear regression梯度下降的线性回归)
2.1 Model representation
Housing Prices**(Portland, OR)** 房价预测
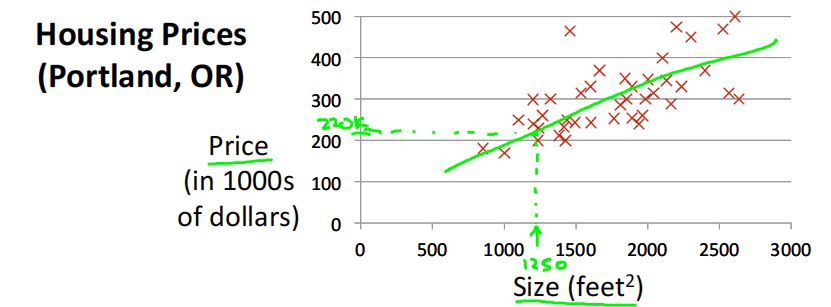
Supervised Learning监督学习: Given the "right answer" for each example in the data.
Regression Problem回归: Predict realLvalued output实值输出
Classification分类: Discrete-valued output离散值输出
Training set of housing prices (Portland, OR)训练集
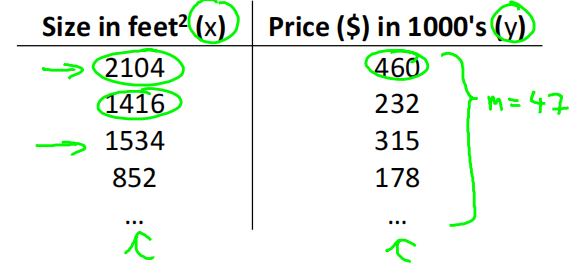
Notation:
𝑚 = Number of training examples
𝑥 = "input" variable / features
𝑦 = "output" variable / "target" variable
(𝑥, 𝑦) - one training example
(𝑥 (𝑖) , 𝑦 (𝑖) ) - i th training example
𝑚 代表训练集中实例的数量
𝑥 代表特征/输入变量
𝑦 代表目标变量/输出变量
(𝑥, 𝑦) 代表训练集中的实例
(𝑥 (𝑖) , 𝑦 (𝑖) ) 代表第𝑖 个观察实例
ℎ 代表学习算法的解决方案或函数也称为假设(hypothesis)
算法工作模式
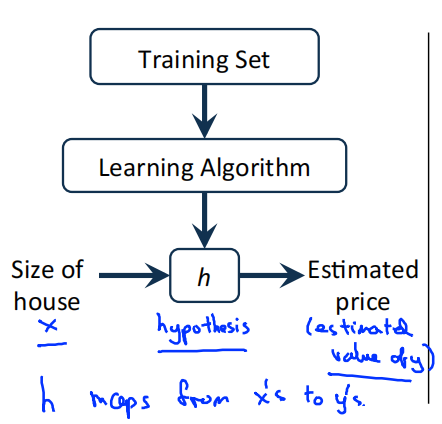
一个监督学习算法的工作模式:将训练集(房屋价格)喂给学习算法,然后输出一个函数,用ℎ 表示,ℎ 代表hypothesis(假设)。ℎ 根据输入的数量𝑥 值来得出变量𝑦 值,数量𝑥 值对于房子的大小,变量𝑦 值对应房子的价格。ℎ 是一个从数量𝑥 到变量𝑦 的函数映射。
How do we represent h?

一种可能的表达方式:
由于只含有一个特征/输入变量,因此这样的问题叫做
Linear regression with one variable 一元线性回归
Univariate linear regression 单变量线性回归
2.2 Cost function 代价函数
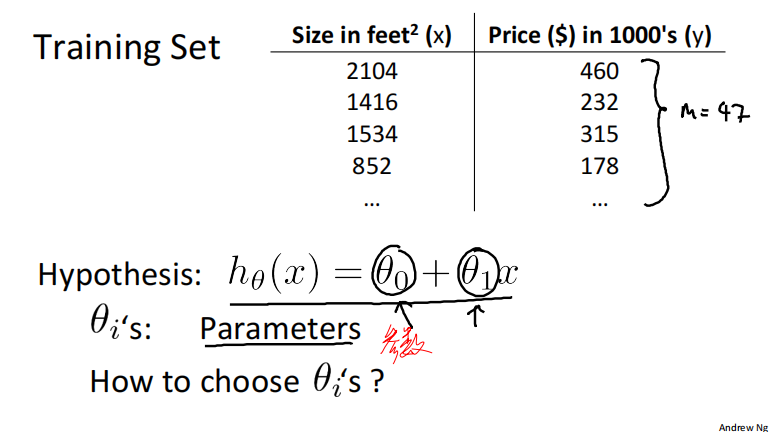
有一个线性回归的训练集,m代表训练样本的数量,本例中m =47。假设函数为如下线性函数形式:
参数𝜃_0, 𝜃_1对应函数图像的截距和斜率,不同𝜃_0, 𝜃_1对应着不同的函数图像。
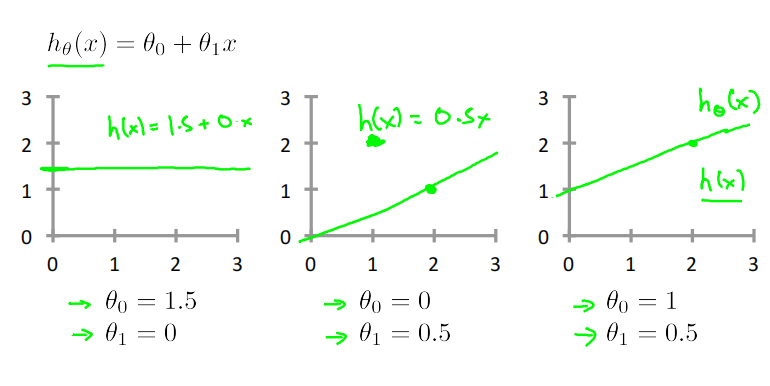
如何选择合适的𝜃_0, 𝜃_1,使得ℎ_𝜃(𝑥)与训练集中的y最接近呢?
目标为选择出使得建模误差(modeling error)的平方和最小的模型参数,即使得代价函数
𝐽(𝜃_0, 𝜃_1) = \\frac{1}{2m} \\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)\^2}
最小
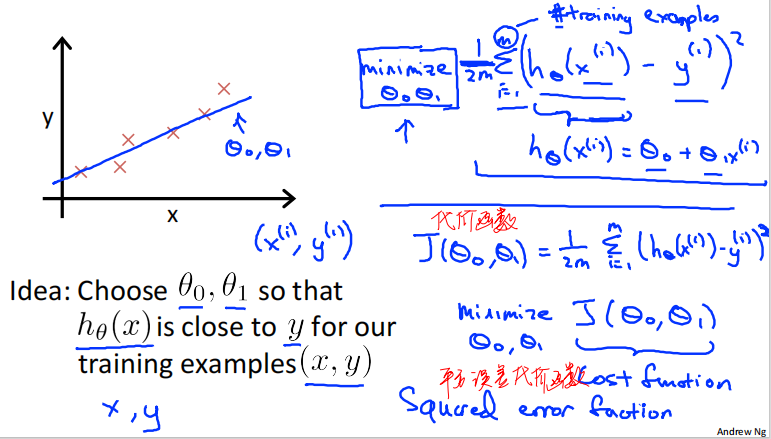
cost function 代价函数,也称为
squared error function 平方误差函数
2.3 Cost function intuition I
在2.2中,我们讨论了代价函数
𝐽(𝜃_0, 𝜃_1) = \\frac{1}{2m} \\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)\^2}

原代价函数中含有两个参数𝜃_0, 𝜃_1,现将问题简化,令𝜃_0=0,则代价函数退化为J(𝜃_1),即函数只含𝜃_1一个参数。
𝐽(𝜃_1) = \\frac{1}{2m} \\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)\^2} \\\\=\\frac{1}{2m} \\sum_{i=1}\^{m}{(𝜃_1𝑥\^𝑖 − 𝑦\^𝑖)\^2}
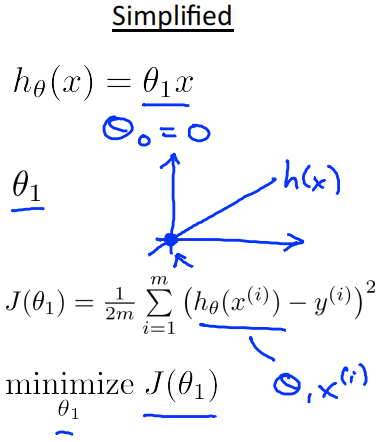
当𝜃_1=1时,𝐽(𝜃_1) =\\frac{1}{2m}(0\^2+0\^2+0\^2)=0 ,即𝐽(1) =0 。
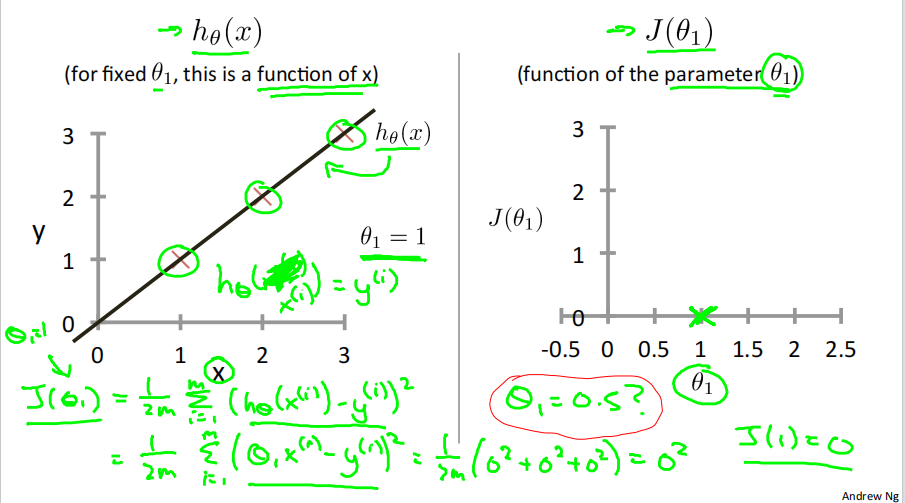
当𝜃_1=0.5时,𝐽(𝜃_1) =\\frac{1}{2m}((0.5-1)\^2+(1-2)\^2+(1.5-3)\^2)=0.58 ,即𝐽(0.5) =0.58 。
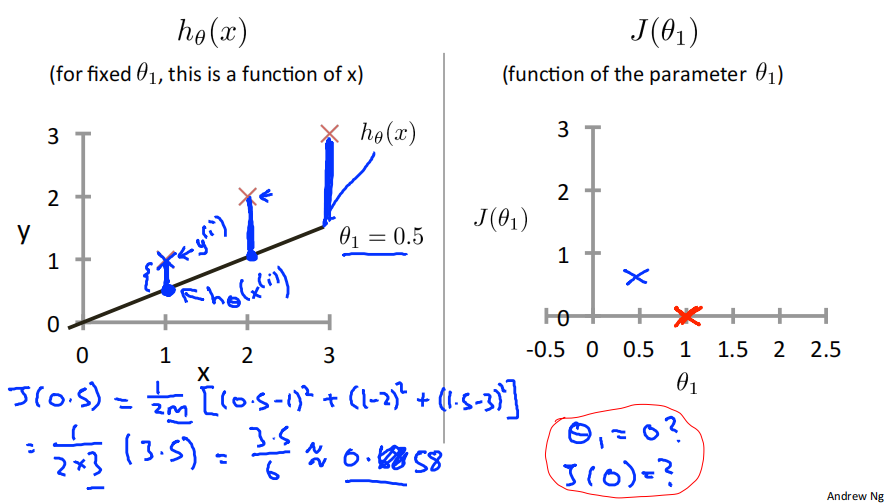
当𝜃_1=0时,𝐽(𝜃_1) =\\frac{1}{2m}(1\^2+2\^2+3\^2)=2.3 ,即𝐽(0) =2.3 。
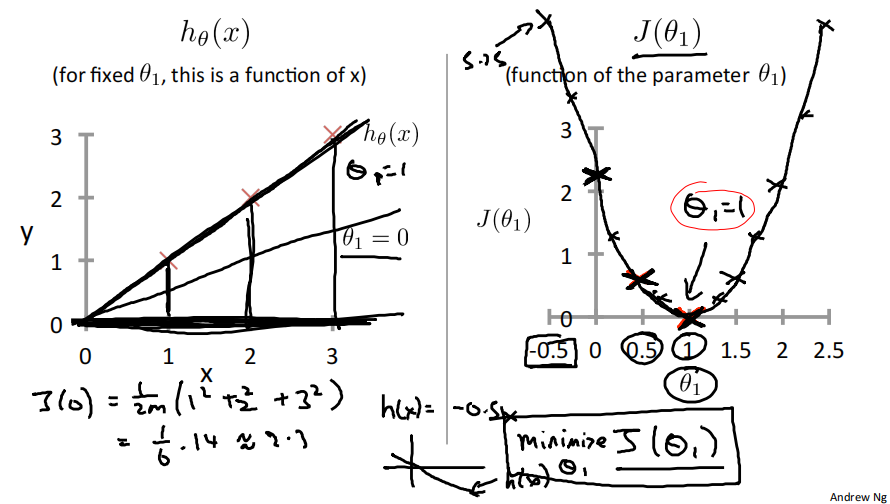
从以上例子可以看出,𝐽(𝜃_1) 为关于𝜃_1 的一元二次函数,存在最低点,即存在𝜃_1 ,使得𝐽(𝜃_1) 取得最小值。
2.4 Cost function intuition II
Hypothesis: ℎ_𝜃(𝑥) = 𝜃_0 + 𝜃_1x
Parameters: 𝜃_0, 𝜃_1
Cost Function: 𝐽(𝜃_0, 𝜃_1) = \\frac{1}{2m} \\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)\^2}
Goal: minimize{𝜃_0, 𝜃_1} 𝐽(𝜃_0, 𝜃_1)
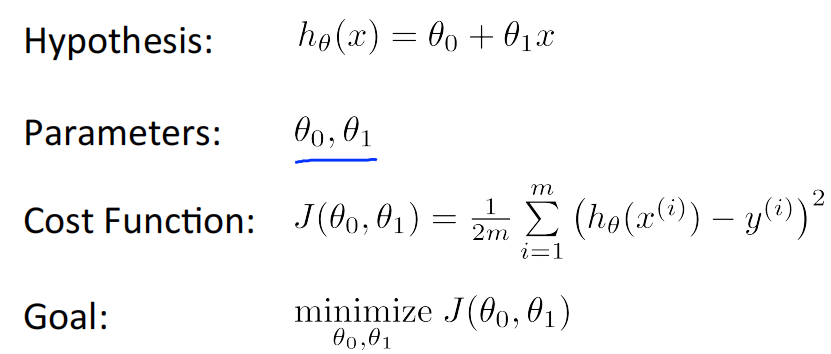
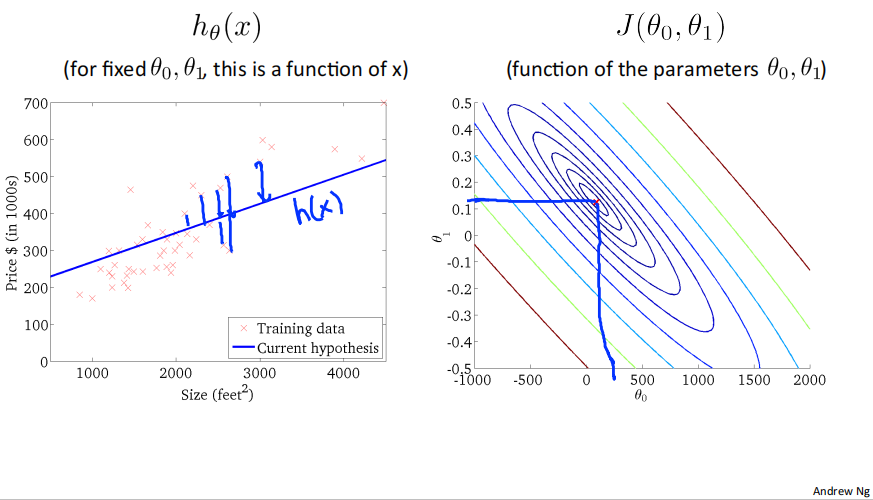
when 𝜃_0=50, 𝜃_1=0.06, ℎ_𝜃(𝑥) = 50 + 0.06x, and 𝐽(𝜃_0, 𝜃_1) as follows:
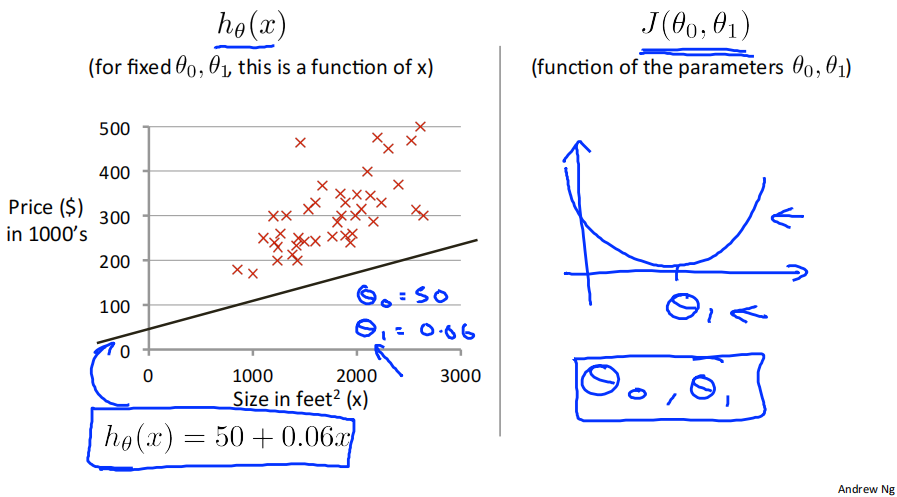
二维代价函数𝐽(𝜃_0, 𝜃_1)对应的图像是在三维空间中的等高线图(Contour plots / Contour figures).图像中存在一个最低点。
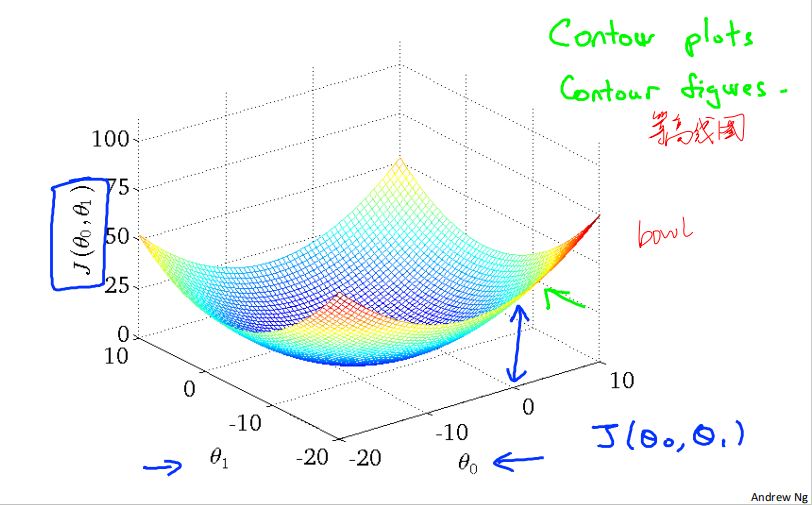
下面是几个例子,展示了位于等高线上不同点对应的ℎ_𝜃(𝑥)图像:
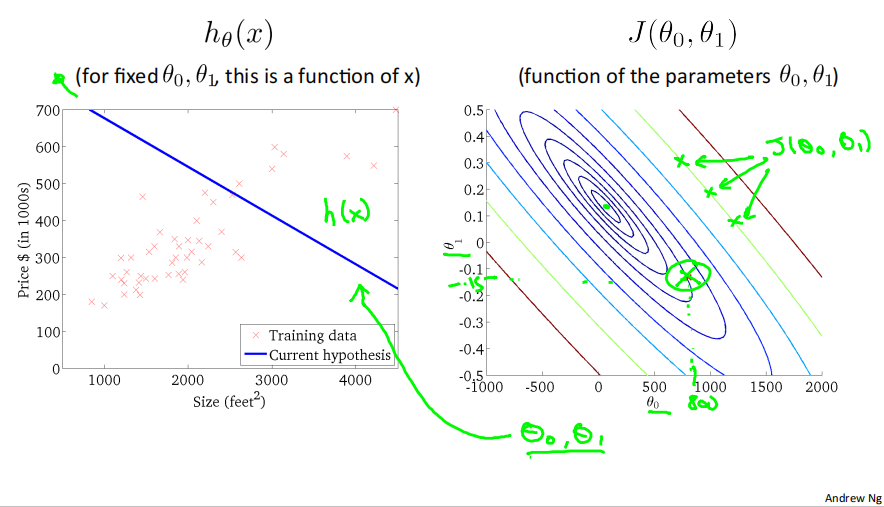
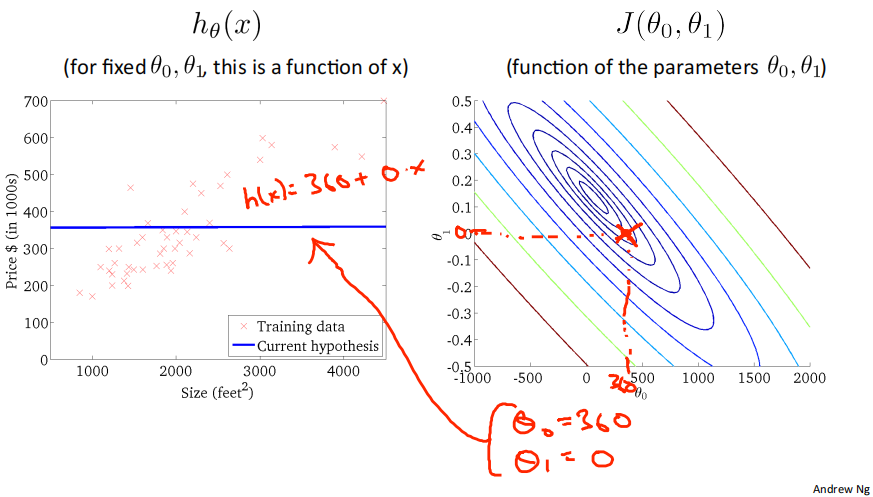
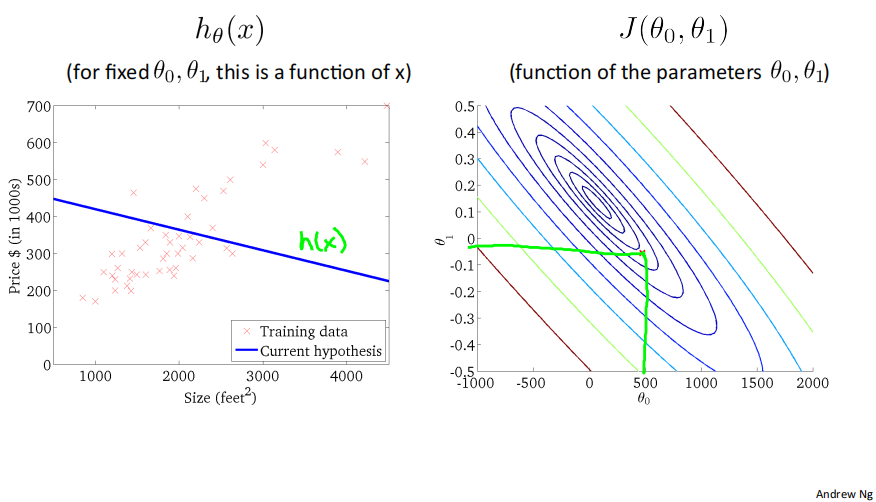
2.5 Gradient descent梯度下降
We have some function 𝐽(𝜃_0, 𝜃_1)
• Start with some 𝜃_0, 𝜃_1
• Keep changing 𝜃_0, 𝜃_1 to reduce 𝐽(𝜃_0, 𝜃_1) until we hopefully end up at a minimum
可拓展至有n个参数的情况。
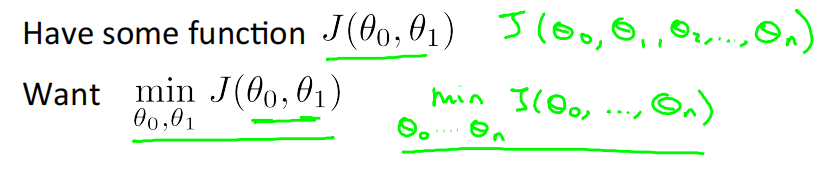
选择不同的初始参数组合,可能会找到不同的局部最小值。
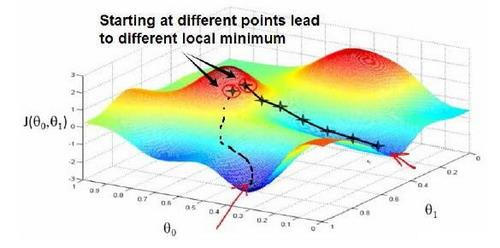
通俗来说,过程就是:
想象一下,你正站在这座红色山上------它就像你脑海中公园里的一座山。在梯度下降算法中,我们要做的,就是先原地转一圈,仔细观察四周,然后问自己:要想尽快下山,该往哪个方向迈出一连串小碎步?一旦确定了方向,你就朝那儿走一小步。
接着,从这个新的位置再次环顾四周,判断下一步往哪里走能最快下降。然后又迈出一小步,如此反复......一步一步,直到你逐渐接近那个局部的最低点。
Gradient descent algorithm
公式:
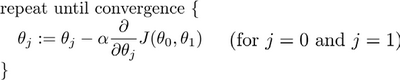
其中:=为赋值符号。𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

需要注意的是,在梯度下降算法运行过程中,需要同步更新𝜃_0和𝜃_1。若不同步更新,会导致错误。

2.6 Gradient descent intuition
Gradient descent algorithm

derivative导数项 can be a positive number or negative number, 对应positive slope or negative slope.
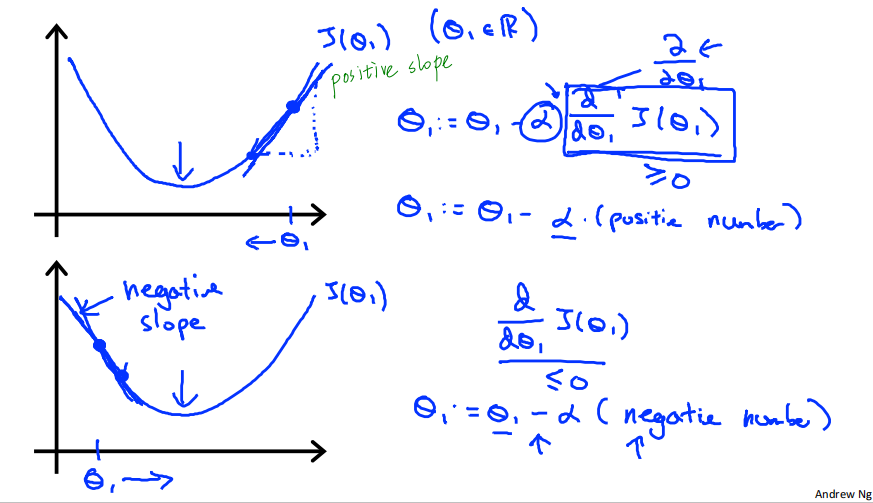
learning rate学习率 𝑎 is also important.
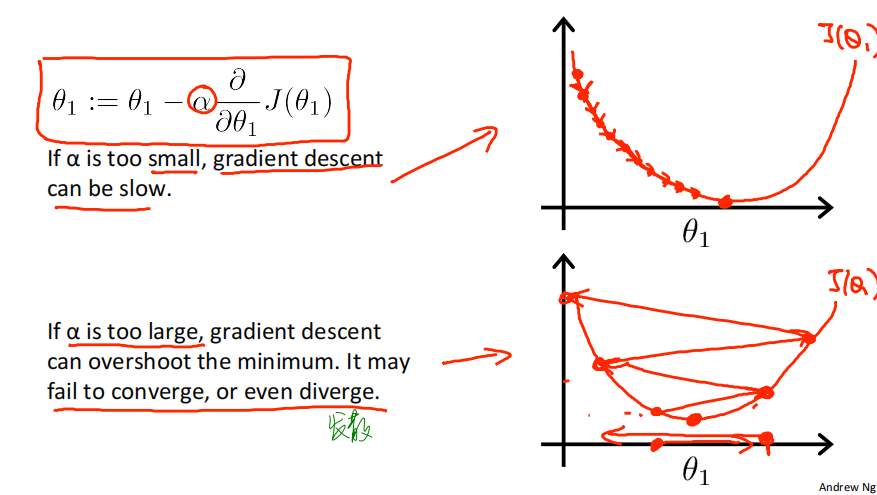
If 𝑎 is too small, gradient descent can be slow.
If 𝑎 is too large, gradient descent can overshoot the minimum. It may fail to converge收敛, or even diverge发散.
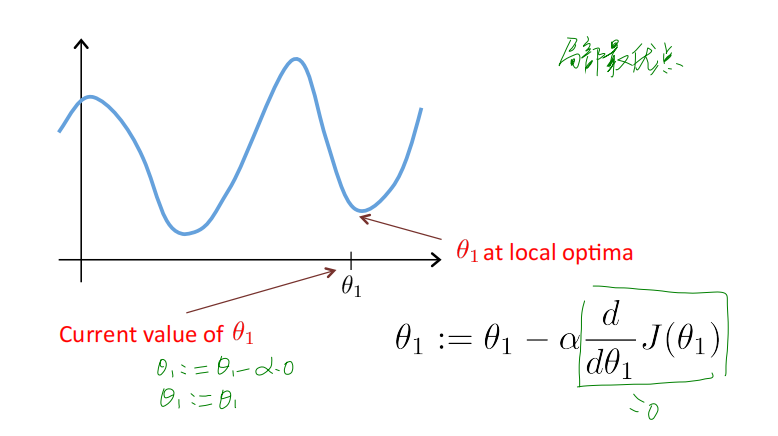
一个值得思考的问题:如果一开始𝜃_1的取值就位于局部最低点呢,运行算法会得到什么样的变化呢?
实际上,当𝜃_1的取值位于局部最低点时,公式中的导数项为0,算法做的就是将𝜃_1的取值再次赋给𝜃_1,实际上对𝜃_1的取值没有任何改变。
另外一个值得思考的问题:需要逐渐减小学习率𝑎吗?
答案是:不需要!
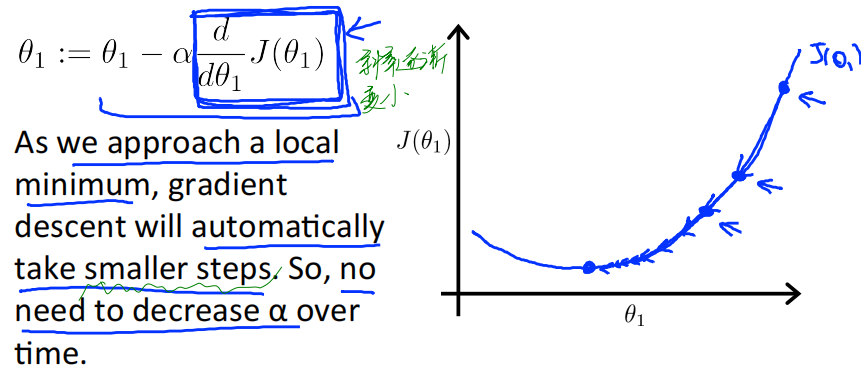
Gradient descent can converge to a local minimum, even with the learning rate 𝑎 fixed.
As we approach a local minimum, gradient descent will automatically take smaller steps. So, no need to decrease 𝑎 over time.
2.7 Gradient descent for linear regression梯度下降的线性回归
梯度下降算法和线性回归算法比较:

对先前讨论的线性回归问题使用梯度下降算法,关键在于求出代价函数的导数,即:
\\frac{𝜕}{𝜕𝜃_𝑗}𝐽(𝜃_0, 𝜃_1) = \\frac{𝜕}{𝜕𝜃_𝑗}\\frac{1}{2m}\\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)\^2} \\\\=\\frac{𝜕}{𝜕𝜃_𝑗}\\frac{1}{2m}\\sum_{i=1}\^{m}{(𝜃_0+𝜃_1𝑥\^𝑖 − 𝑦\^𝑖)\^2}
j=0 时:\\frac{𝜕}{𝜕𝜃_0}𝐽(𝜃_0, 𝜃_1) =\\frac{1}{m}\\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)}
j=1 时:\\frac{𝜕}{𝜕𝜃_1}𝐽(𝜃_0, 𝜃_1) =\\frac{1}{m}\\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)𝑥\^𝑖}
则算法改写为:
repeat until convergence{
𝜃_0 := 𝜃_0-𝑎\\frac{1}{m}\\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)} \\\\𝜃_1 := 𝜃_1-𝑎\\frac{1}{m}\\sum_{i=1}\^{m}{(ℎ_𝜃(𝑥\^𝑖) − 𝑦\^𝑖)𝑥\^𝑖}
}Update 𝜃_0 and 𝜃_1 simultaneously
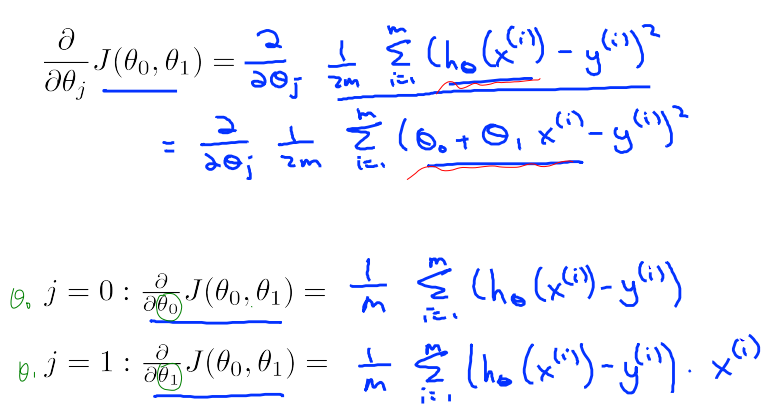

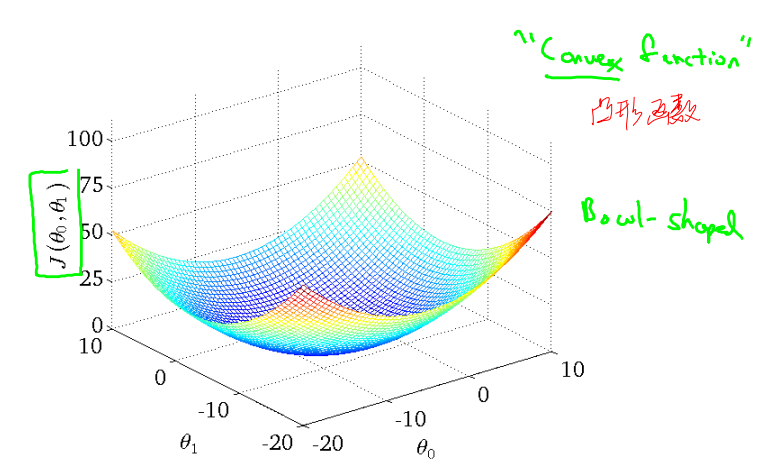
损失函数𝐽(𝜃_0, 𝜃_1) 对应的图像如下:
Convex function 凸型函数 Bowl-shaped
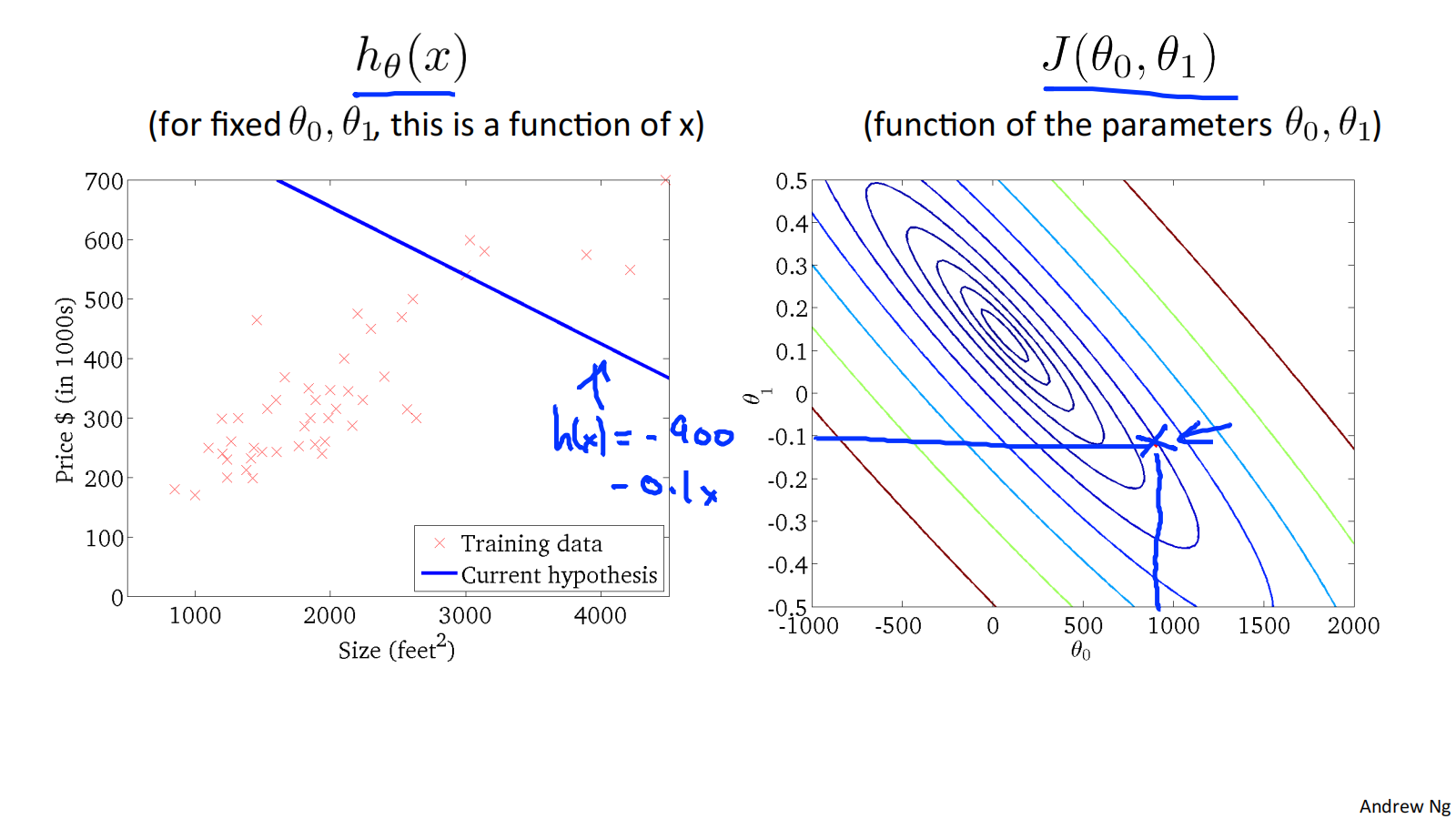
可通过下面的例子体会收敛过程:
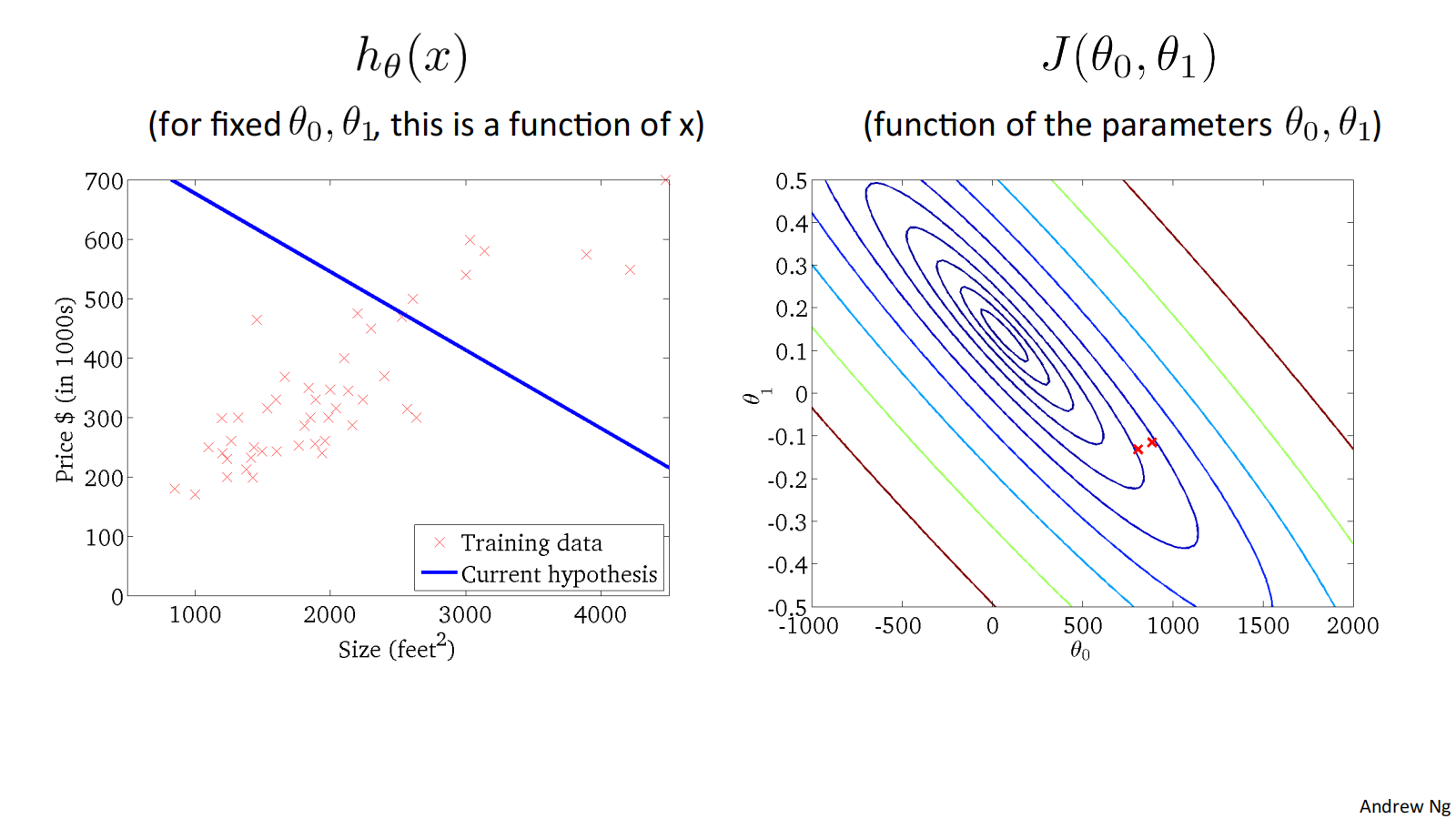
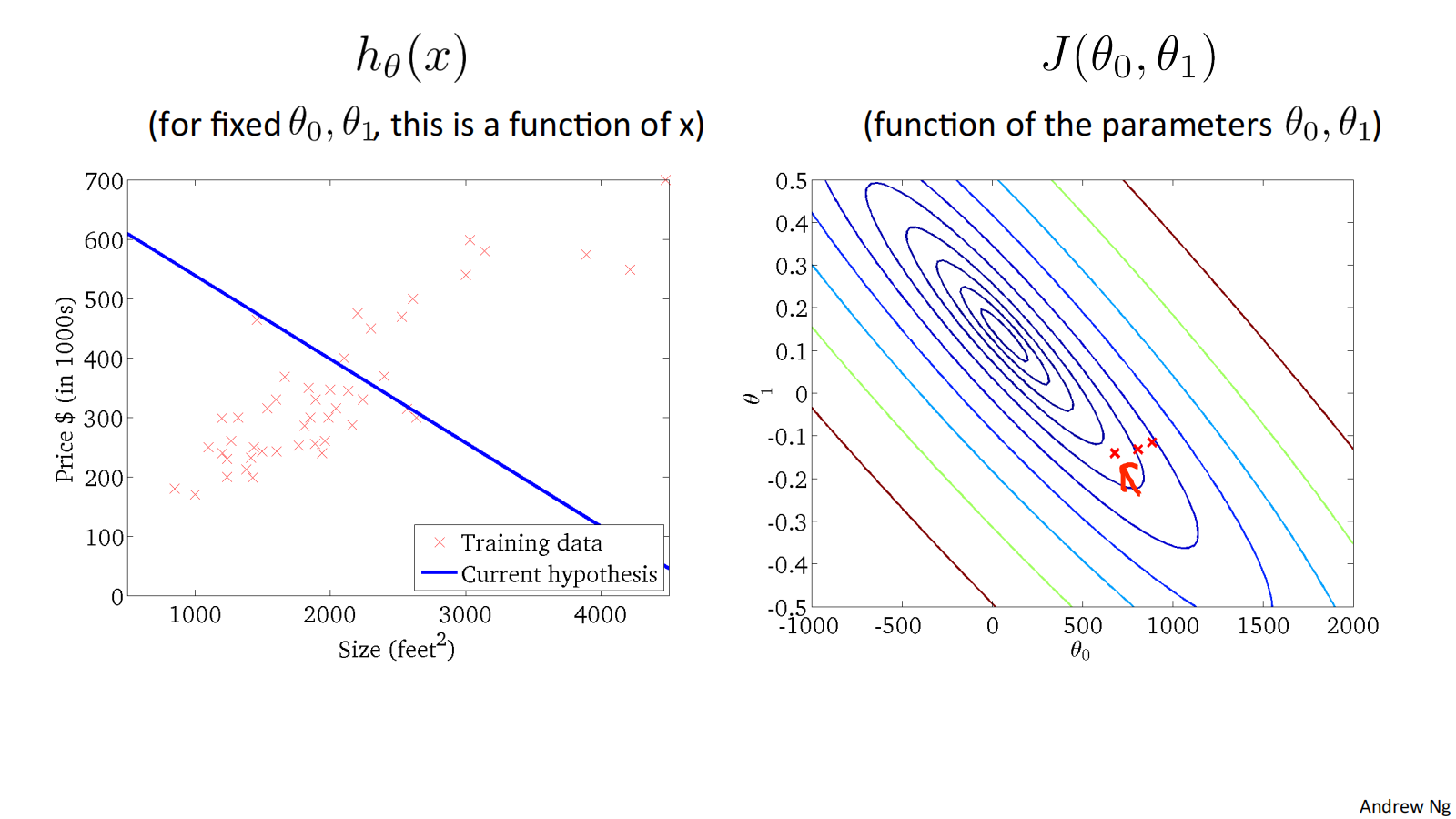
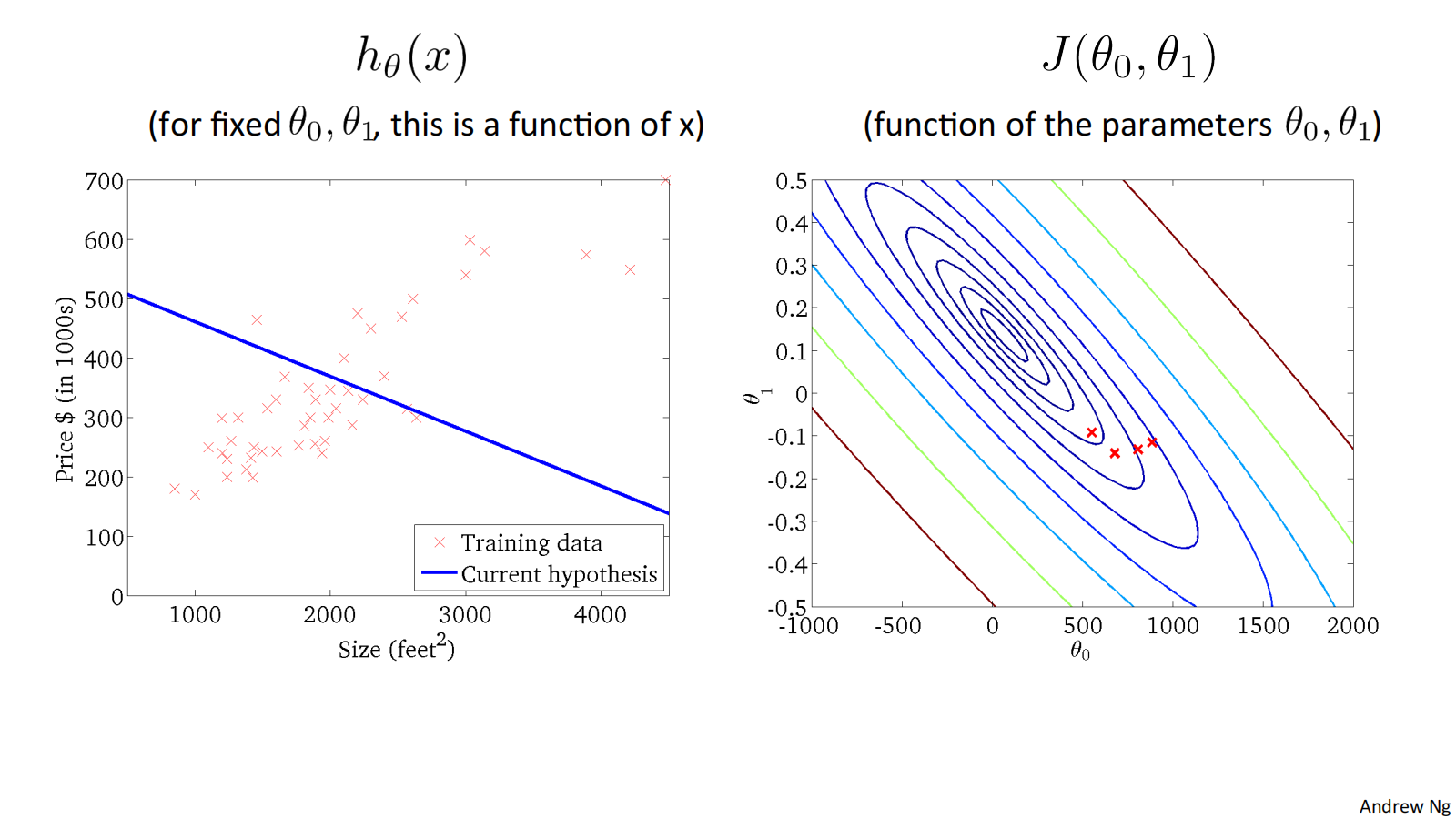
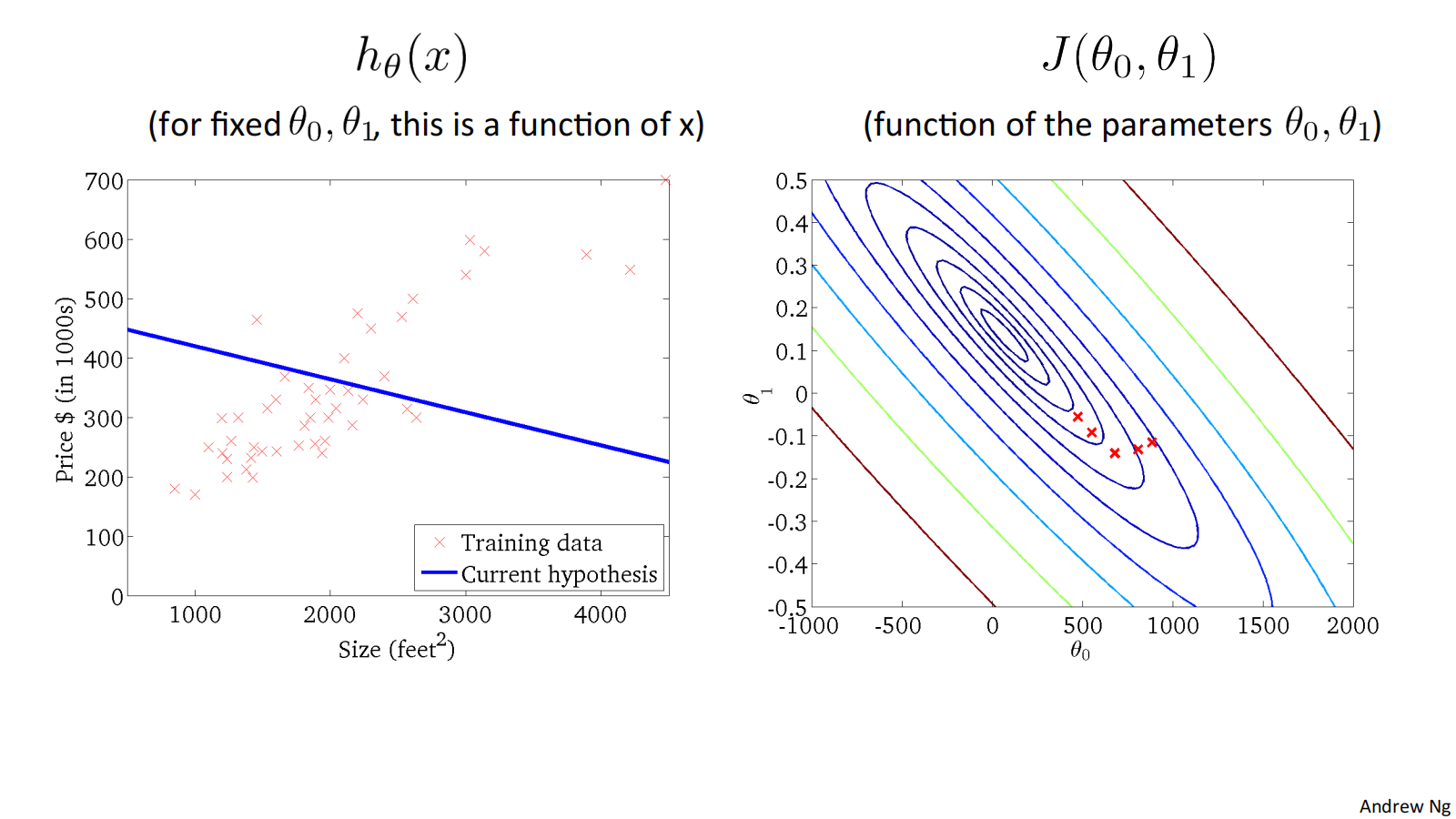
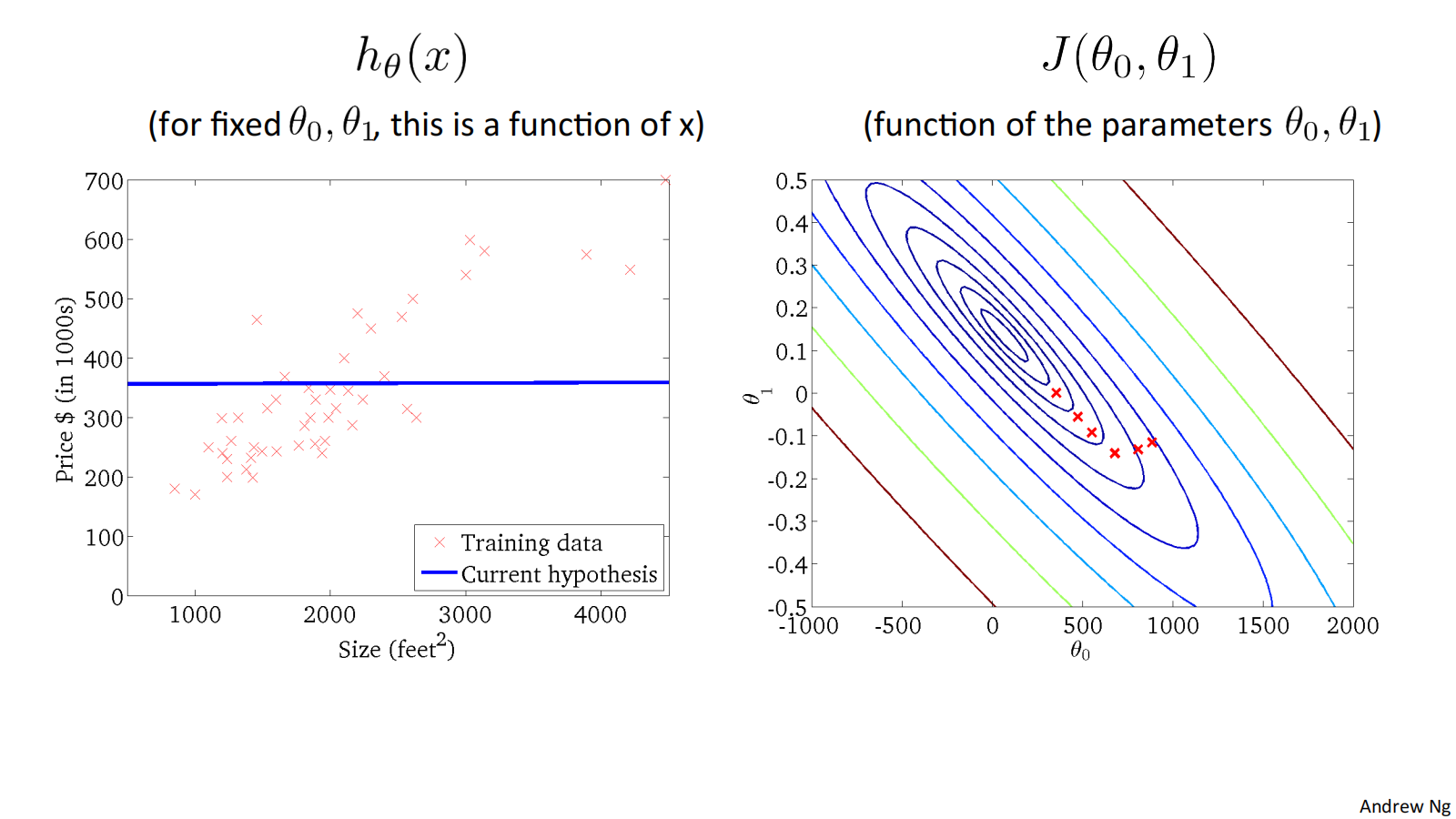
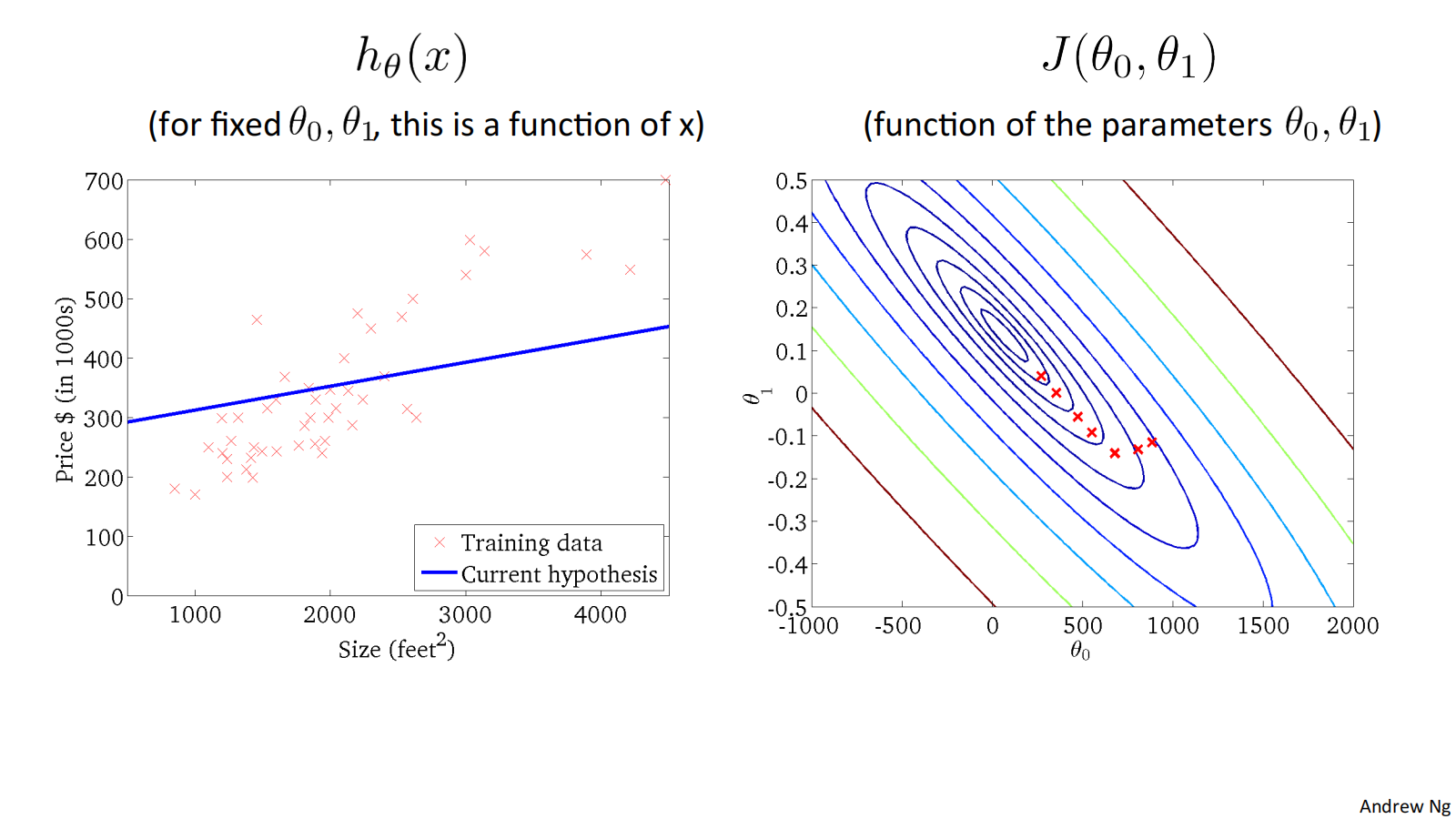
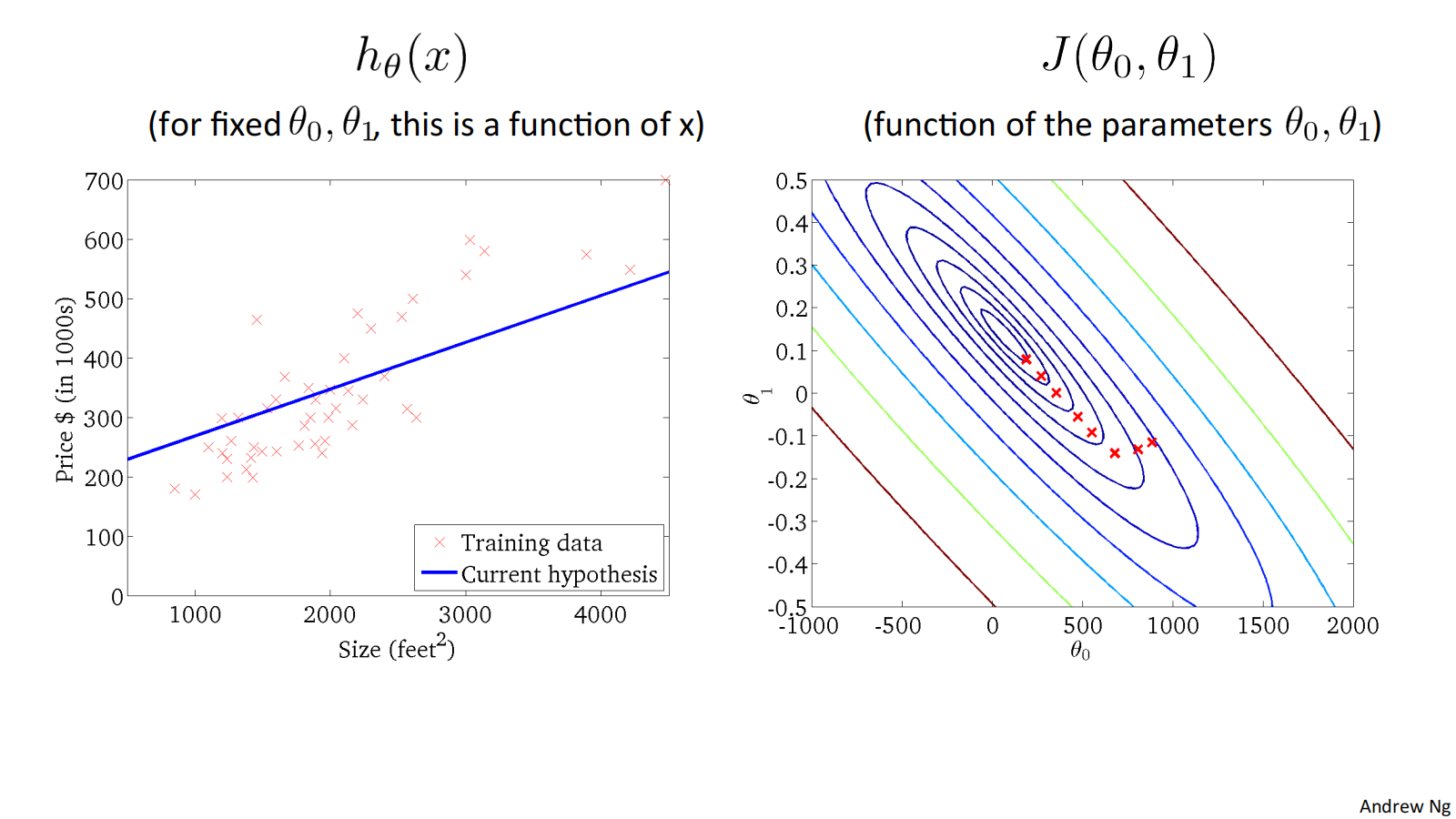
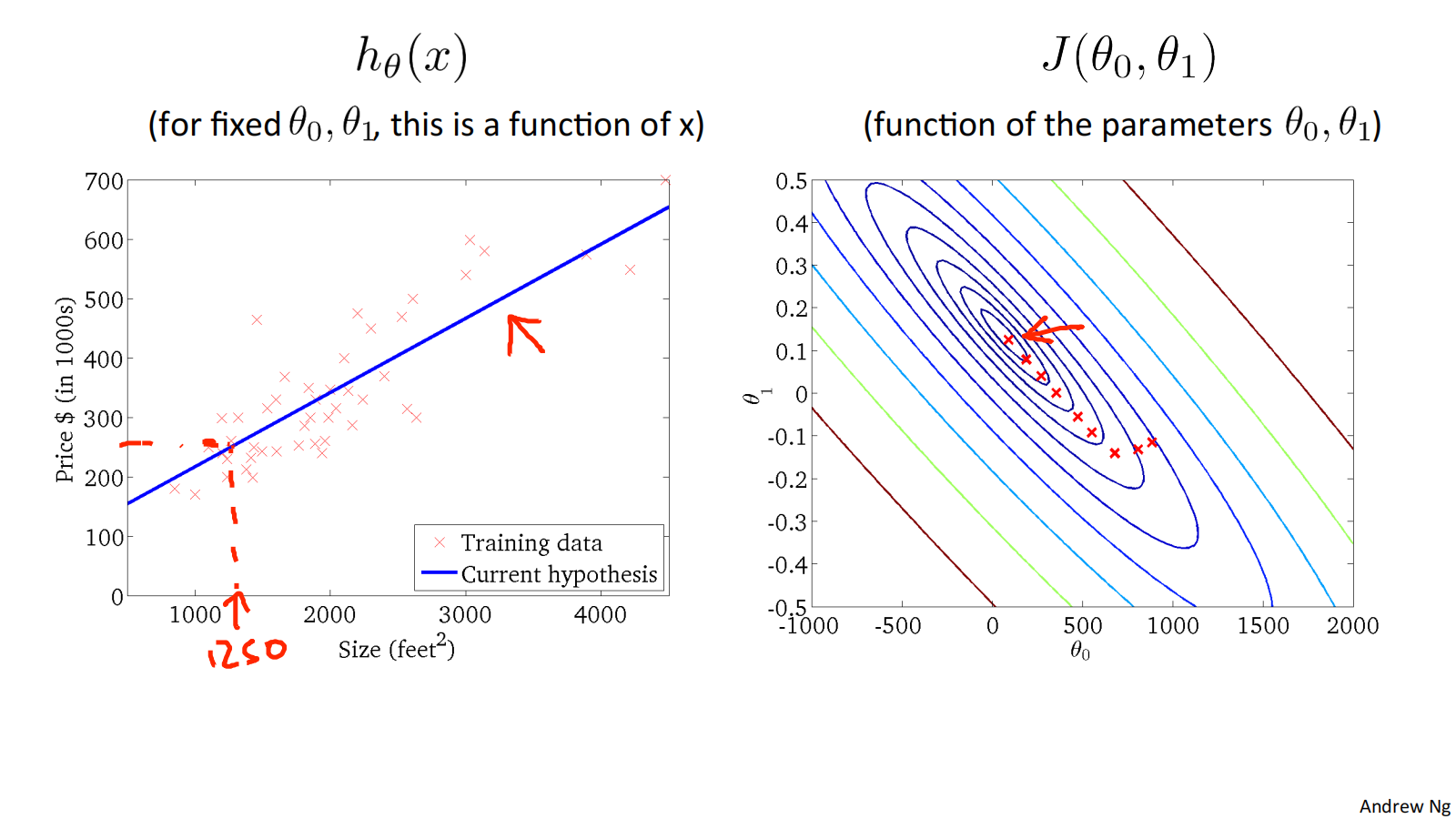
"Batch" Gradient Descent批量梯度下降
"Batch": Each step of gradient descent uses all the training examples. 梯度下降的每一步中,都用到了所有的训练样本
而事实上,有时也有其他类型的梯度下降法,不是这种"批量"型的,不考虑整个的训练集,每次只关注训练集中的一些小的子集。在后面的课程中,我们也将介绍这些方法,比如正规方程组法(normal equations).