合并区间（贪心算法）

对于区间问题，我们一般分为两步：

1、排序（左端点或右端点）

2、根据排序后的结果，总结出一些规律，进而得出解决这个问题的策略

本道题实际上是让我们求并集，可以采用左端点排序（排完序可以发现，能够合并的区间都是连续的）

合并原理可以来看下面的图解：

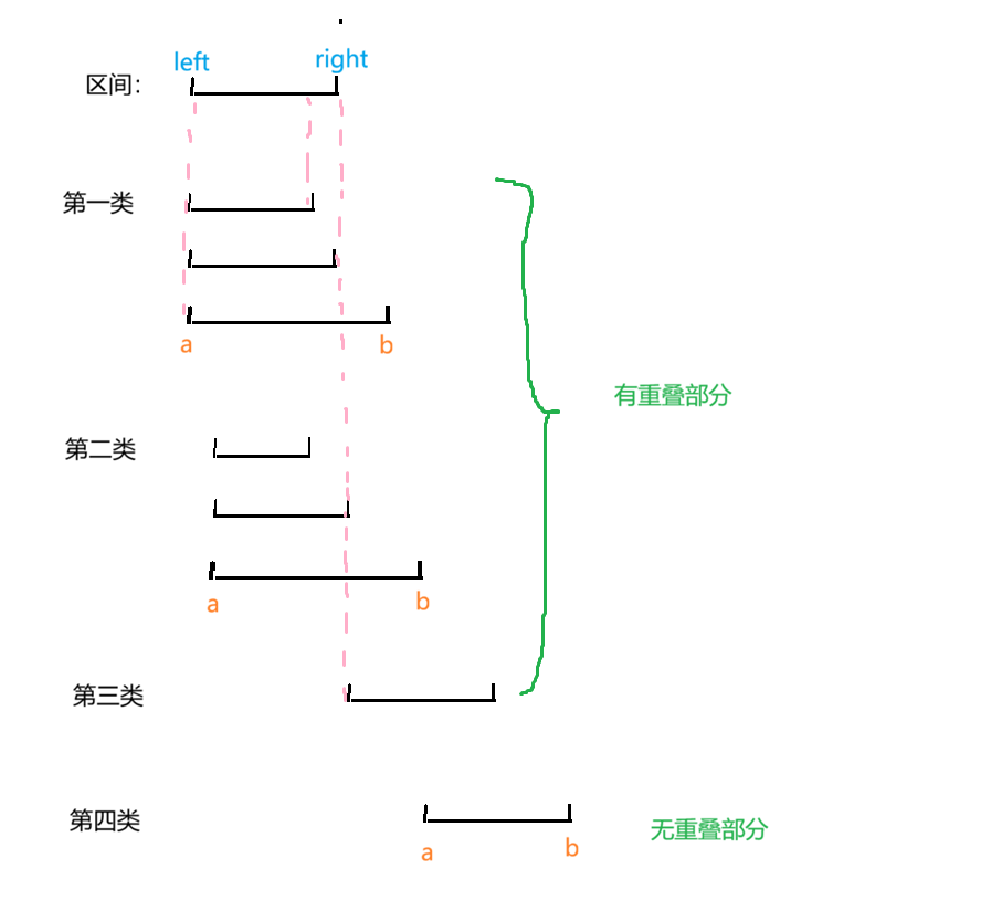
前三类归为有重叠部分：a<=right;

再根据上图可以得出，有交集的时候，合并过程中左端点依旧是left，而右端点需要选择较大值max(right,b).

对于无重叠部分：a>right

这时我们先把给定区间加入到结果数组中，然后让left=a,right=b，针对后面的区间在进行上述合并过程。

以上是本道题的算法原理，下面来看具体代码实现：

java 复制代码

class Solution {
    public int[][] merge(int[][] intervals) {
        //先按照左端点排序
        Arrays.sort(intervals,(v1,v2)->{
            //每次拿出这个两个数比较，其实就是给定二维数组中的两个区间
            //我们是按照左端点排序，所以拿v[0],如果按照右端点排序，拿v[1]
            return v1[0]-v2[0];
        });
        //合并区间，求并集
        //先把第一个区间拿出来作为基准区间然后和后面的区间进行合并
        int left=intervals[0][0],right=intervals[0][1];
        List<int[]> ret=new ArrayList<>(); //添加结果
        //遍历一遍数组
        for(int i=0;i<intervals.length;i++){
            //每次拿到一个区间之后，我们先得到他的左右端点
            int a=intervals[i][0],b=intervals[i][1];
            //分情况讨论
            if(a<=right){ //有重叠部分，合并求并集
                right=Math.max(right,b);//左端点不变，右端点更新为较大值
            }else{ //不能合并，把之前的区间加入到结果中去
                ret.add(new int[]{left,right}); 
                left=a;
                right=b;//拿新的区间去合并
            }
        }
        //循环结束之后我们要把最后一个区间手动添加到结果中，因为left和right更新到最后一个区间时，我们是把前一个区间添加到结果去，此时循环已经结束
        ret.add(new int[]{left,right});
        return ret.toArray(new int[0][]); //要把ret转换为二维数组格式 ，int[0][]让方法自动匹配大小 
    }
}