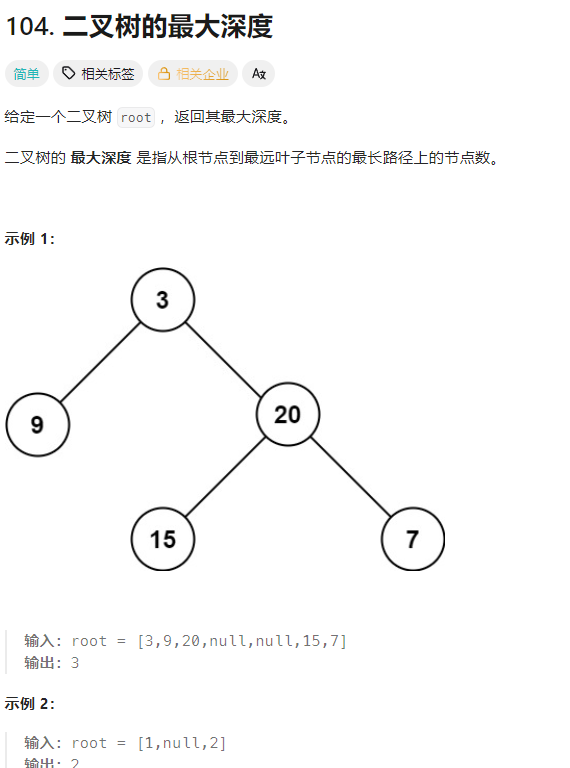
leetcode hot100 104. 二叉树的最大深度 easy 递归dfs 层序遍历bfs

一棵树的最大深度 = 111 (根节点自己) + 左右子树深度中的最大值。

递归解法（自底向上）

时间复杂度：O(n)O(n)O(n)。每个节点都要问一遍。

空间复杂度：O(height)O(height)O(height) 取决于树的高度

原函数maxDepth的定义是：

输入：一个根节点。
输出：一个代表深度的整数。

可以直接用原函数递归

什么时候需要定义辅助函数？

最大深度：子问题返回的是答案（数字），父函数定义也是返回数字，正好。
中序遍历：子问题要做的是动作（填表），父函数定义是返回list，但不需要每次都返回整个表，只是要部分值

python 复制代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:

        # 1. 递归出口：如果节点为空，深度就是 0
        if not root:
            return 0

        # 2. 递归获取左子树的最大深度
        left_height =  self.maxDepth(root.left)

        # 3. 递归获取右子树的最大深度
        right_height =  self.maxDepth(root.right)

        return max(left_height, right_height) + 1

自顶向下（层序遍历）

剥洋葱：剥掉一层，计数器加 111，直到剥完。

时间复杂度：O(n)O(n)O(n)。每个节点都要问一遍。

空间复杂度：O(width)O(width)O(width)。取决于树最宽的那一层节点数。

弹出最左元素：

如用list列表：pop(0)
如果用 collections.deque( $root$ ) 双端队列：popleft()

python 复制代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:

        if not root:
            return 0


        # 每一层
        queue = [root]  # 初始层，顶层
        depth = 0

        # 把这层元素弹出，
        while queue:
            depth += 1
            for i in range(len(queue)):
                node = queue.pop(0)  # 每次弹出最左边 (队首)元素

                # 并加入弹出元素的左右子树
                if node.left: 
                    queue.append(node.left)
                if node.right: 
                    queue.append(node.right)

        return depth