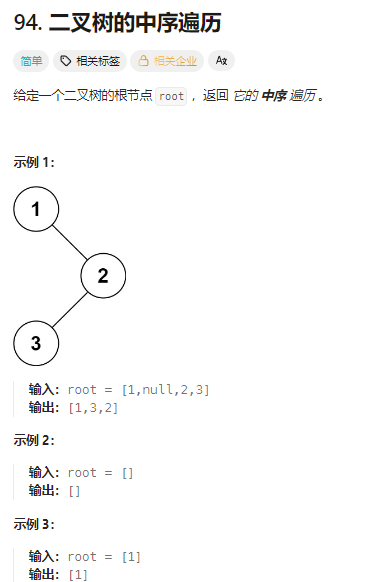
leetcode hot100 94. 二叉树的中序遍历 easy 递归 dfs

踩坑记录2026-02-01 21:58

中序遍历（Inorder Traversal）：左 - 根 - 右

这意味着对于每一棵子树，

先访问左子树
然后访问根节点
最后访问右子树。

递归解法（最直观）

既然是"左-根-右"，就按照这个顺序调用函数即可

原题inorderTraversal函数定义是：

输入：一个根节点。

输出：一个列表 List $int$

直接调用 self.inorderTraversal(root.left)，它会返回一个完整的列表。

而我们只是想把数字填到一个公共的盒子（res）里，而不是每次都造一个新盒子。

辅助函数 inorderdfs 的作用就是：它不返回列表，它只负责干活（把值 append 到外面的 res 列表里）。

python 复制代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:

        res = []

        def inorderdfs(node):
            if not node:
                return None
            
            # 递归
            inorderdfs(node.left)   # 左子树
            res.append(node.val)  # 根节点
            inorderdfs(node.right)  # 右子树

        inorderdfs(root)
        return res

时间复杂度：O(n)O(n)O(n) 。每个节点都会被访问且仅被访问一次。
空间复杂度：O(n)O(n)O(n) 。在最坏情况下（树呈链状），递归深度或栈的高度会达到 nnn。

自底向上

程序是一直钻到最深的左节点，然后才开始收集第一个数字。这给人一种"从最底层开始处理"的感觉。

python 复制代码

dfs(node.left)     # 1. 钻到底
res.append(node.val) # 2. 出来时再捡起路上的果实
dfs(node.right)    # 3. 转向