LSTM详细介绍（基于股票收盘价预测场景）

本文围绕「股票收盘价时序预测」场景（输入：10天股票收盘价数据，输出：第11天股票收盘价数据，训练集1000行原始数据），详细讲解LSTM（Long Short-Term Memory，长短期记忆网络）的核心原理、内部结构、逐步骤运算逻辑（含输入输出矩阵维度）、训练过程（正向传播+反向传播），全程结合实战场景拆解，避免抽象，方便后续回顾查阅。

核心定位：LSTM是一种改进型循环神经网络（RNN），解决了传统RNN在长时序数据中容易出现的梯度消失/梯度爆炸问题，能够有效捕捉时序数据中的长期依赖关系------这一特性恰好适配股票数据的时序特性（前N天的价格趋势、波动规律会影响第N+1天的价格），是股票时序预测中最常用的深度学习模型之一。

一、场景前提与核心定义（奠定基础）

在讲解LSTM内部结构前，先明确本文贯穿始终的股票预测场景参数和核心定义，避免后续混淆。

1.1 股票预测场景核心参数

原始数据：1000行按时间正序排列的股票收盘价（单变量，无其他特征；后续扩展多特征场景：收盘价+成交量+开盘价）；
预测任务：单步回归预测（用前10天的收盘价，预测第11天的收盘价）；
样本切分：按滑动窗口（步长=1，时间步=10）切分，最终得到 1000-10=990 个训练样本；
LSTM核心参数：神经元数（隐藏层维度） n h = 32 n_h=32 nh=32（工程常用值，可调整为16/64等）；
模型结构：LSTM层（时序特征提取）+ 全连接Dense层（预测映射）。

1.2 核心术语定义（必懂）

时间步（timesteps）：每个输入样本的时序长度，本文中 T = 10 T=10 T=10（10天收盘价）；
特征数（features）：每个时间步的输入特征数量，单特征 n x = 1 n_x=1 nx=1，多特征 n x = 3 n_x=3 nx=3；
样本数（samples）：切分后的独立训练样本数量，本文中为990；
细胞状态（Cell State, C t C_t Ct）：LSTM的「长期记忆」，用于存储时序数据中的长期依赖信息，核心是线性更新，避免梯度消失；
隐藏状态（Hidden State, h t h_t ht）：LSTM的「短期记忆」，传递当前时间步的特征信息，同时作为下一个时间步的输入；
门控（Gates）：LSTM的核心组件，用于筛选、控制信息的传递与丢弃，包括遗忘门、输入门、输出门；
参数共享：LSTM的所有时间步，共享一套门控权重和偏置，大幅减少参数量，避免过拟合。

1.3 LSTM输入输出核心格式（硬要求）

LSTM作为时序神经网络，对输入数据的维度有严格要求（TensorFlow/Keras默认格式，PyTorch仅维度顺序不同，核心一致），格式为「三维张量」：

i n p u t _ s h a p e = ( s a m p l e s , t i m e s t e p s , f e a t u r e s ) input\_shape = (samples, timesteps, features) input_shape=(samples,timesteps,features)

单特征场景（仅收盘价）：输入维度为 ( 990 , 10 , 1 ) (990, 10, 1) (990,10,1)；
多特征场景（收盘价+成交量+开盘价）：输入维度为 ( 990 , 10 , 3 ) (990, 10, 3) (990,10,3)；
输出维度（单步预测）：LSTM层输出最后一个时间步的隐藏状态，维度为 ( 990 , 32 ) (990, 32) (990,32)，再通过Dense层映射为 ( 990 , 1 ) (990, 1) (990,1)（对应990个样本的第11天收盘价预测值）。

二、LSTM内部结构详解（核心部分）

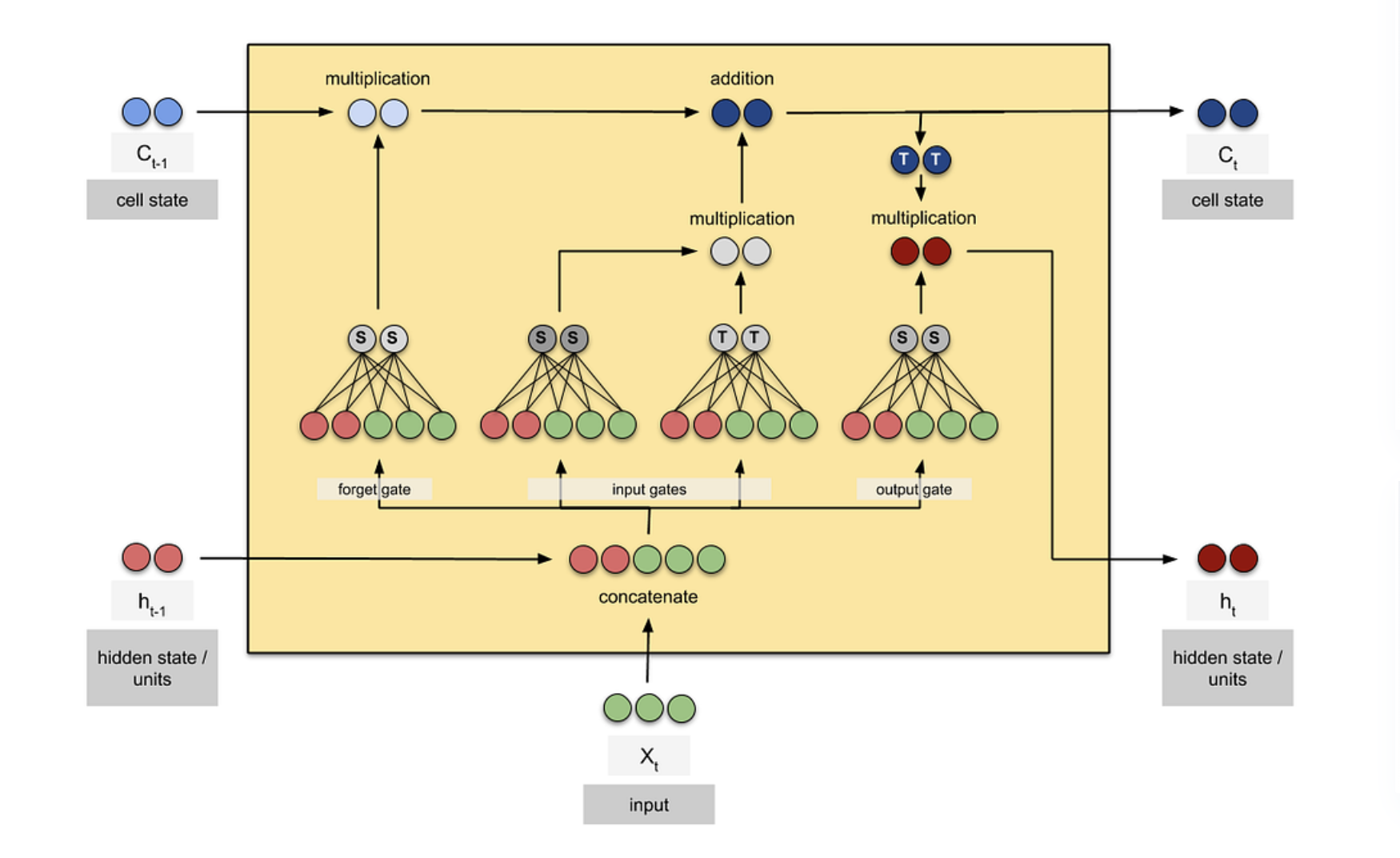
LSTM的内部结构核心是「3个门控（遗忘门、输入门、输出门）+ 1个候选细胞状态 + 1个细胞状态 + 1个隐藏状态」，所有组件协同工作，实现「筛选历史信息、保留当前有用信息、输出有效特征」的功能。

核心逻辑：LSTM通过门控的「开关控制」（sigmoid激活函数，输出0~1），决定哪些历史信息被丢弃、哪些当前信息被保留；通过细胞状态的线性更新，实现长期依赖的记忆；通过隐藏状态，传递当前时间步的特征信息。

以下按「单时间步运算」拆解（所有时间步运算逻辑一致，仅输入数据不同），结合股票场景、运算公式、输入输出矩阵维度，逐一讲解每个组件。

2.1 单时间步核心变量（贯穿所有组件）

假设当前处理第 t t t个时间步（ t t t的范围为1~10，对应10天收盘价），定义以下核心变量（维度均为单样本单时间步，批处理维度后续补充）：

x t x_t xt：第 t t t个时间步的输入特征向量，单特征时为 ( 1 , ) (1,) (1,)，多特征时为 ( 3 , ) (3,) (3,)；
h t − 1 h_{t-1} ht−1：第 t − 1 t-1 t−1个时间步的隐藏状态，维度为 ( 32 , ) (32,) (32,)（由神经元数 n h n_h nh决定）；
C t − 1 C_{t-1} Ct−1：第 t − 1 t-1 t−1个时间步的细胞状态，维度为 ( 32 , ) (32,) (32,)（与隐藏状态维度一致）；
W f , W i , W C , W o W_f, W_i, W_C, W_o Wf,Wi,WC,Wo：分别为遗忘门、输入门、候选细胞状态、输出门的权重矩阵（可训练）；
b f , b i , b C , b o b_f, b_i, b_C, b_o bf,bi,bC,bo：分别为遗忘门、输入门、候选细胞状态、输出门的偏置（可训练）；
σ \sigma σ：sigmoid激活函数（输出0~1，实现门控开关，0=完全丢弃，1=完全保留）；
t a n h tanh tanh：双曲正切激活函数（输出-1~1，用于归一化候选细胞状态和隐藏状态）；
$h t − 1 , x t \] \[h_{t-1}, x_t\] \[ht−1,xt\]：将上一隐藏状态与当前输入拼接后的向量，单特征时维度为 ( 32 + 1 , ) = ( 33 , ) (32+1,)= (33,) (32+1,)=(33,)，多特征时为 ( 32 + 3 , ) = ( 35 , ) (32+3,)= (35,) (32+3,)=(35,)。$

2.2.1 核心功能

遗忘门的作用是「筛选历史细胞状态中的信息」，决定哪些历史信息（如前几天的股票价格波动）需要被丢弃，哪些需要被保留，适配股票数据的趋势变化（比如大跌时，丢弃前几天的小涨无关信息）。

2.2.2 运算公式

f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) ft=σ(Wf⋅[ht−1,xt]+bf)

运算逻辑：拼接向量 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 与遗忘门权重 W f W_f Wf 做矩阵乘法，加上偏置 b f b_f bf，再通过sigmoid激活函数，得到遗忘门输出 f t f_t ft；
核心说明：矩阵乘法的核心是「将拼接后的输入特征，映射到与神经元数一致的维度」，偏置用于调整输出偏移。

2.2.3 输入输出矩阵维度（关键）

场景	输入 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 维度	权重 W f W_f Wf 维度	偏置 b f b_f bf 维度	输出 f t f_t ft 维度
单特征（ n x = 1 n_x=1 nx=1）	(33,)	(32, 33)	(32,)	(32,)
多特征（ n x = 3 n_x=3 nx=3）	(35,)	(32, 35)	(32,)	(32,)

2.2.4 股票场景解读

假设 t = 5 t=5 t=5（第5天），股票收盘价大跌，此时遗忘门输出 f t f_t ft中，对应「前4天小涨信息」的元素会接近0（丢弃），对应「前4天整体下跌趋势」的元素会接近1（保留），确保历史有用信息不被丢弃。

2.3 组件2：输入门（Input Gate）------ 保留当前有用信息

2.3.1 核心功能

输入门的作用是「筛选当前时间步的输入信息」，决定哪些当前时间步的特征（如第 t t t天的收盘价、成交量）需要被保留，并存入后续的细胞状态中。

2.3.2 运算公式

i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) it=σ(Wi⋅[ht−1,xt]+bi)

运算逻辑：与遗忘门完全一致，仅权重 W i W_i Wi和偏置 b i b_i bi不同（可训练参数独立）；
核心说明：输入门与遗忘门协同工作，遗忘门处理历史信息，输入门处理当前信息，共同决定细胞状态的更新。

2.3.3 输入输出矩阵维度

场景	输入 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 维度	权重 W i W_i Wi 维度	偏置 b i b_i bi 维度	输出 i t i_t it 维度
单特征（ n x = 1 n_x=1 nx=1）	(33,)	(32, 33)	(32,)	(32,)
多特征（ n x = 3 n_x=3 nx=3）	(35,)	(32, 35)	(32,)	(32,)

2.3.4 股票场景解读

假设 t = 8 t=8 t=8（第8天），股票收盘价上涨且成交量骤增（强趋势信号），此时输入门输出 i t i_t it中，对应「收盘价上涨」「成交量骤增」的元素会接近1（重点保留），对应「小幅波动」的元素会接近0（忽略），确保当前关键信息被存入细胞状态。

2.4 组件3：候选细胞状态（Candidate Cell State, C t ~ \tilde{C_t} Ct~）------ 生成当前新信息

2.4.1 核心功能

候选细胞状态的作用是「生成当前时间步的原始新信息」，将上一隐藏状态的历史信息与当前输入的特征信息结合，生成可供后续筛选的原始信息，是细胞状态更新的基础。

2.4.2 运算公式

C t ~ = t a n h ( W C ⋅ [ h t − 1 , x t ] + b C ) \tilde{C_t} = tanh(W_C \cdot [h_{t-1}, x_t] + b_C) Ct~=tanh(WC⋅[ht−1,xt]+bC)

运算逻辑：与门控运算逻辑一致，拼接向量 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 与权重 W C W_C WC 做矩阵乘法，加偏置 b C b_C bC 后，通过tanh激活函数（将值压缩到-1~1，避免数值溢出）；
核心区别：门控用sigmoid（实现开关），候选细胞状态用tanh（实现信息归一化），生成的是「未经过筛选的原始新信息」。

2.4.3 输入输出矩阵维度

场景	输入 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 维度	权重 W C W_C WC 维度	偏置 b C b_C bC 维度	输出 C t ~ \tilde{C_t} Ct~ 维度
单特征（ n x = 1 n_x=1 nx=1）	(33,)	(32, 33)	(32,)	(32,)
多特征（ n x = 3 n_x=3 nx=3）	(35,)	(32, 35)	(32,)	(32,)

2.4.4 股票场景解读

C t ~ \tilde{C_t} Ct~ 会结合第 t − 1 t-1 t−1天的隐藏状态（前 t − 1 t-1 t−1天的趋势信息）和第 t t t天的收盘价（当前信息），生成第 t t t天的原始时序信息，比如「前 t − 1 t-1 t−1天下跌+第 t t t天上涨」的组合信息，后续会通过输入门筛选，保留有用部分。

2.5 组件4：细胞状态（Cell State, C t C_t Ct）------ 更新长期记忆（核心）

2.5.1 核心功能

细胞状态是LSTM的「长期记忆核心」，通过「遗忘门筛选后的历史信息 + 输入门筛选后的当前新信息」的线性叠加，实现长期记忆的更新，也是LSTM解决传统RNN梯度消失的关键（线性运算无激活函数，梯度可稳定传递）。

2.5.2 运算公式

C t = f t ⊙ C t − 1 + i t ⊙ C t ~ C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C_t} Ct=ft⊙Ct−1+it⊙Ct~

运算逻辑：仅做「逐元素乘法（ ⊙ \odot ⊙）+ 逐元素加法」，无矩阵乘法（所有输入维度一致，元素级运算）；
核心拆解：
1. f t ⊙ C t − 1 f_t \odot C_{t-1} ft⊙Ct−1：遗忘门 f t f_t ft 与上一细胞状态 C t − 1 C_{t-1} Ct−1 逐元素相乘，筛选并保留历史长期记忆中的有用信息；
2. i t ⊙ C t ~ i_t \odot \tilde{C_t} it⊙Ct~：输入门 i t i_t it 与候选细胞状态 C t ~ \tilde{C_t} Ct~ 逐元素相乘，筛选并保留当前时间步的有用新信息；
3. 二者相加：得到当前时间步的细胞状态 C t C_t Ct，即「更新后的长期记忆」。

2.5.3 输入输出矩阵维度

细胞状态的输入输出维度「完全一致」，仅由神经元数 n h n_h nh决定，与特征数无关，具体如下：

场景	输入1（ f t ⊙ C t − 1 f_t \odot C_{t-1} ft⊙Ct−1）维度	输入2（ i t ⊙ C t ~ i_t \odot \tilde{C_t} it⊙Ct~）维度	输出 C t C_t Ct 维度
单特征/多特征	(32,)	(32,)	(32,)

2.5.4 股票场景解读

比如处理完10个时间步（10天收盘价）后，最终的细胞状态 C 10 C_{10} C10 会存储「这10天的完整价格趋势、关键波动点」等长期信息，比如「前3天下跌、中间4天横盘、后3天上涨」的整体趋势，为后续预测第11天价格提供长期时序支撑。

2.6 组件5：输出门（Output Gate）------ 筛选输出有效特征

2.6.1 核心功能

输出门的作用是「筛选当前细胞状态中的信息」，决定哪些长期记忆信息（细胞状态 C t C_t Ct）需要被输出，作为当前时间步的隐藏状态 h t h_t ht，传递给下一个时间步，或作为最终的特征输出。

2.6.2 运算公式

o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) ot=σ(Wo⋅[ht−1,xt]+bo)

运算逻辑：与遗忘门、输入门完全一致，仅权重 W o W_o Wo和偏置 b o b_o bo不同（独立可训练）；
核心说明：输出门筛选的是「细胞状态中的长期记忆信息」，确保输出的隐藏状态仅包含对后续时间步/预测有用的特征。

2.6.3 输入输出矩阵维度

场景	输入 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 维度	权重 W o W_o Wo 维度	偏置 b o b_o bo 维度	输出 o t o_t ot 维度
单特征（ n x = 1 n_x=1 nx=1）	(33,)	(32, 33)	(32,)	(32,)
多特征（ n x = 3 n_x=3 nx=3）	(35,)	(32, 35)	(32,)	(32,)

2.6.4 股票场景解读

处理完第10个时间步后，输出门 o 10 o_{10} o10 会筛选细胞状态 C 10 C_{10} C10 中的信息，仅保留「对预测第11天收盘价有用的趋势特征」（如最后3天的上涨幅度、成交量变化），过滤无关的波动信息，确保隐藏状态 h 10 h_{10} h10 是有效特征。

2.7 组件6：隐藏状态（Hidden State, h t h_t ht）------ 传递短期记忆

2.7.1 核心功能

隐藏状态是LSTM的「短期记忆」，也是LSTM的核心输出特征：

作为「下一个时间步（ t + 1 t+1 t+1）」的输入 h t h_t ht，传递当前时间步的特征信息；单步预测场景中，最后一个时间步的隐藏状态 h 10 h_{10} h10，会作为LSTM层的最终输出，传递给Dense层做预测。

2.7.2 运算公式

h t = o t ⊙ t a n h ( C t ) h_t = o_t \odot tanh(C_t) ht=ot⊙tanh(Ct)

运算逻辑：先对当前细胞状态 C t C_t Ct 做tanh激活（归一化到-1~1），再与输出门 o t o_t ot 逐元素相乘，得到当前时间步的隐藏状态 h t h_t ht；
核心说明：隐藏状态是「输出门筛选后的细胞状态信息」，既包含长期记忆的有效部分，也包含当前时间步的特征，是时序特征的核心载体。

2.7.3 输入输出矩阵维度

与细胞状态一致，仅由神经元数 n h n_h nh决定，与特征数无关：

场景	输入1（ o t o_t ot）维度	输入2（ t a n h ( C t ) tanh(C_t) tanh(Ct)）维度	输出 h t h_t ht 维度
单特征/多特征	(32,)	(32,)	(32,)

2.7.4 股票场景解读

第10个时间步的隐藏状态 h 10 h_{10} h10，是「10天收盘价时序特征」的浓缩载体，包含了这10天的价格趋势、波动规律、关键拐点等信息，后续通过Dense层的线性映射，将这32维的特征向量，转化为1维的第11天收盘价预测值。

2.8 单时间步完整运算流程（汇总）

将上述6个组件按运算顺序汇总，单时间步（第 t t t步）的完整流程为：

拼接上一隐藏状态 h t − 1 h_{t-1} ht−1 与当前输入 x t x_t xt，得到拼接向量 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt]；
计算遗忘门 f t f_t ft，筛选历史细胞状态信息；
计算输入门 i t i_t it，筛选当前输入信息；
计算候选细胞状态 C t ~ \tilde{C_t} Ct~，生成当前原始新信息；
更新细胞状态 C t C_t Ct（长期记忆）： f t ⊙ C t − 1 + i t ⊙ C t ~ f_t \odot C_{t-1} + i_t \odot \tilde{C_t} ft⊙Ct−1+it⊙Ct~；
计算输出门 o t o_t ot，筛选细胞状态中的有效信息；
更新隐藏状态 h t h_t ht（短期记忆）： o t ⊙ t a n h ( C t ) o_t \odot tanh(C_t) ot⊙tanh(Ct)，传递给下一时间步 t + 1 t+1 t+1。

2.9 多时间步运算逻辑（贴合10天预测场景）

本文股票场景中，时间步 T = 10 T=10 T=10（10天收盘价），多时间步的运算逻辑为「串行执行」：

初始状态：第1个时间步（ t = 1 t=1 t=1）无 h 0 h_{0} h0 和 C 0 C_{0} C0，模型默认初始化为全0向量（维度(32,)）；
串行执行：从 t = 1 t=1 t=1 到 t = 10 t=10 t=10，依次执行上述单时间步运算，每个时间步的 h t h_t ht 和 C t C_t Ct 作为下一个时间步的 h t − 1 h_{t-1} ht−1 和 C t − 1 C_{t-1} Ct−1；
最终输出： t = 10 t=10 t=10 时，LSTM层输出隐藏状态 h 10 h_{10} h10（维度(990, 32)，990为样本数），细胞状态 C 10 C_{10} C10 不输出（仅用于内部记忆更新）；
参数共享：所有10个时间步，共享一套 W f / W i / W C / W o W_f/W_i/W_C/W_o Wf/Wi/WC/Wo 和 b f / b i / b C / b o b_f/b_i/b_C/b_o bf/bi/bC/bo，模型仅需学习一套参数，减少参数量。

三、LSTM训练逻辑（正向传播+反向传播）

结合股票预测场景，讲解LSTM的完整训练流程------核心是「正向传播生成预测值→计算误差→反向传播更新参数」，重点说明反向传播如何处理LSTM的门控参数和隐藏状态/细胞状态的梯度。

3.1 正向传播（Forward Propagation）

正向传播的核心是「从输入数据到预测值的完整链路」，结合本文股票场景，步骤如下：

数据预处理：将1000行原始收盘价归一化（缩放到[0,1]），按滑动窗口切分为990个样本，重塑为LSTM输入格式 ( 990 , 10 , 1 ) (990, 10, 1) (990,10,1)（单特征）；
LSTM层运算：对每个样本，从 t = 1 t=1 t=1 到 t = 10 t=10 t=10 串行执行单时间步运算，输出最后一个时间步的隐藏状态 h 10 h_{10} h10，维度为 ( 990 , 32 ) (990, 32) (990,32)；
Dense层映射：将 h 10 h_{10} h10 输入全连接层（1个神经元），通过线性运算 y p r e d = W d ⋅ h 10 + b d y_{pred} = W_d \cdot h_{10} + b_d ypred=Wd⋅h10+bd，生成预测值 y p r e d y_{pred} ypred，维度为 ( 990 , 1 ) (990, 1) (990,1)（对应990个样本的第11天收盘价预测值）；
计算损失：采用均方误差（MSE）计算预测值 y p r e d y_{pred} ypred 与真实标签 y t r u e y_{true} ytrue（第11天真实收盘价）的误差，即 L o s s = 1 2 ( y p r e d − y t r u e ) 2 Loss = \frac{1}{2}(y_{pred} - y_{true})^2 Loss=21(ypred−ytrue)2。

3.2 反向传播（Backward Propagation）

反向传播的核心是「通过链式法则，将损失误差反向传递，更新模型所有可训练参数」，解决「如何将误差传递到LSTM的每个门控参数」的问题，步骤如下（重点简化，避免过于复杂的数学推导）：

3.2.1 核心前提

模型的可训练参数分为两类：

Dense层参数：权重 W d W_d Wd（维度(1, 32)）、偏置 b d b_d bd（维度(1,)）；LSTM层参数：4个门控的权重 W f / W i / W C / W o W_f/W_i/W_C/W_o Wf/Wi/WC/Wo、4个门控的偏置 b f / b i / b C / b o b_f/b_i/b_C/b_o bf/bi/bC/bo。

反向传播的误差源头是 L o s s Loss Loss，核心是「从Dense层反向传递到LSTM层，再按时间步反向传递到每个门控参数」。

3.2.2 第一步：更新Dense层参数

计算Loss对预测值 y p r e d y_{pred} ypred 的梯度： ∂ L o s s ∂ y p r e d = y p r e d − y t r u e \frac{\partial Loss}{\partial y_{pred}} = y_{pred} - y_{true} ∂ypred∂Loss=ypred−ytrue；
计算Loss对 W d W_d Wd 和 b d b_d bd 的梯度（链式法则）：
- ∂ L o s s ∂ W d = ∂ L o s s ∂ y p r e d ⋅ h 10 T \frac{\partial Loss}{\partial W_d} = \frac{\partial Loss}{\partial y_{pred}} \cdot h_{10}^T ∂Wd∂Loss=∂ypred∂Loss⋅h10T（ h 10 T h_{10}^T h10T 是 h 10 h_{10} h10 的转置，维度(32, 990)）；
- ∂ L o s s ∂ b d = ∂ L o s s ∂ y p r e d \frac{\partial Loss}{\partial b_d} = \frac{\partial Loss}{\partial y_{pred}} ∂bd∂Loss=∂ypred∂Loss；
参数更新：用梯度下降（或Adam优化器）更新 W d W_d Wd 和 b d b_d bd，公式为 W d = W d − α ⋅ ∂ L o s s ∂ W d W_d = W_d - \alpha \cdot \frac{\partial Loss}{\partial W_d} Wd=Wd−α⋅∂Wd∂Loss（ α \alpha α 为学习率）。

3.2.3 第二步：更新LSTM层参数（核心难点）

LSTM层的反向传播是「按时间步反向遍历」（从 t = 10 t=10 t=10 倒推到 t = 1 t=1 t=1），因为每个时间步的 h t h_t ht 和 C t C_t Ct 依赖上一个时间步的 h t − 1 h_{t-1} ht−1 和 C t − 1 C_{t-1} Ct−1，步骤如下：

初始误差输入：计算Loss对LSTM最终输出 h 10 h_{10} h10 的梯度 ∂ L o s s ∂ h 10 = ∂ L o s s ∂ y p r e d ⋅ W d T \frac{\partial Loss}{\partial h_{10}} = \frac{\partial Loss}{\partial y_{pred}} \cdot W_d^T ∂h10∂Loss=∂ypred∂Loss⋅WdT（维度(990, 32)），作为LSTM反向传播的初始误差；
时间步反向遍历（ t = 10 → t = 1 t=10 \to t=1 t=10→t=1）：
- 对每个时间步 t t t，结合正向传播中记录的中间值（ f t / i t / o t / C t ~ / h t / C t f_t/i_t/o_t/\tilde{C_t}/h_t/C_t ft/it/ot/Ct~/ht/Ct），通过链式法则，计算Loss对当前时间步门控参数（ W f / W i / W C / W o W_f/W_i/W_C/W_o Wf/Wi/WC/Wo）和偏置的梯度；
- 计算Loss对 h t − 1 h_{t-1} ht−1 和 C t − 1 C_{t-1} Ct−1 的梯度，作为下一个（前一个）时间步 t − 1 t-1 t−1 的误差输入；
参数梯度累加：由于所有时间步共享一套LSTM门控参数，需将10个时间步的参数梯度累加，得到Loss对LSTM门控参数的总梯度；
参数更新：用总梯度通过梯度下降，更新LSTM的所有门控权重和偏置。

3.2.4 关键补充（避坑）

细胞状态的梯度：单步预测场景中，最后一个时间步的细胞状态 C 10 C_{10} C10 无后续输出，因此 ∂ L o s s ∂ C 10 = 0 \frac{\partial Loss}{\partial C_{10}} = 0 ∂C10∂Loss=0；
梯度消失缓解：细胞状态的更新是线性运算（无激活函数），梯度可在时间步间稳定传递，大幅缓解了传统RNN的梯度消失问题，适合股票10天的长时序预测；
框架自动处理：开发者无需手动推导梯度计算，TensorFlow/PyTorch等框架会自动记录正向传播的中间值，完成反向传播和参数更新，只需定义损失函数和优化器即可。

3.3 训练闭环（汇总）

股票预测场景中，LSTM的完整训练闭环为：

正向传播：输入10天收盘价→LSTM提取时序特征→Dense层生成第11天预测值→计算Loss；
反向传播：从Loss出发→更新Dense层参数→反向传递误差到LSTM层→按时间步更新LSTM门控参数；
多轮迭代：重复上述步骤（epochs=50~100），直到Loss收敛（预测值与真实值的误差稳定在较小范围）；
模型应用：训练完成后，输入新的10天收盘价，即可通过模型预测第11天的收盘价。

四、场景扩展：多特征股票预测适配

实际股票预测中，仅用收盘价（单特征）的效果有限，通常会加入成交量、开盘价、最高价、最低价等多特征，LSTM的适配逻辑如下（核心是「维度调整」，运算逻辑不变）：

4.1 数据格式调整

输入维度从 ( 990 , 10 , 1 ) (990, 10, 1) (990,10,1) 调整为 ( 990 , 10 , 3 ) (990, 10, 3) (990,10,3)（收盘价+成交量+开盘价， n x = 3 n_x=3 nx=3），每个时间步的输入向量 x t x_t xt 维度为 ( 3 , ) (3,) (3,)。

4.2 运算维度调整

仅拼接向量 [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt] 的维度变化，从单特征的 ( 33 , ) (33,) (33,) 调整为 ( 35 , ) (35,) (35,)（32+3），所有门控的权重矩阵维度同步调整（如 W f W_f Wf 从 ( 32 , 33 ) (32, 33) (32,33) 调整为 ( 32 , 35 ) (32, 35) (32,35)），其余运算步骤、维度规则完全不变。

4.3 核心优势

LSTM会同时读取单时间步的所有特征，联合编码特征间的关联关系（比如「收盘价上涨+成交量骤增」是强趋势信号，「收盘价上涨+成交量萎缩」是弱趋势信号），相比单特征，能捕捉更多股票价格的影响因素，提升预测精度。

五、核心总结（方便快速回顾）

5.1 LSTM核心亮点

解决传统RNN梯度消失问题，通过线性细胞状态实现长期时序记忆，适配股票等长时序数据；
通过3个门控（遗忘门、输入门、输出门）实现信息的筛选与控制，保留有用信息，丢弃无用信息；
参数共享，参数量少，避免过拟合，适合样本量有限的股票预测场景。

5.2 股票场景核心适配点

输入格式：10天收盘价→三维张量 ( s a m p l e s , 10 , 1 ) (samples, 10, 1) (samples,10,1)，多特征扩展为 ( s a m p l e s , 10 , n x ) (samples, 10, n_x) (samples,10,nx)；
运算逻辑：10个时间步串行执行，输出最后一个时间步的隐藏状态，通过Dense层映射为第11天收盘价预测值；
训练关键：定义MSE损失函数和Adam优化器，框架自动完成正向/反向传播，无需手动推导梯度。

5.3 维度计算速记规则

门控（遗忘/输入/输出）+ 候选细胞状态：输入维度 ( n h + n x , ) (n_h + n_x,) (nh+nx,)，权重维度 ( n h , n h + n x ) (n_h, n_h + n_x) (nh,nh+nx)，输出维度 ( n h , ) (n_h,) (nh,)；
细胞状态+隐藏状态：输入输出维度均为 ( n h , ) (n_h,) (nh,)，与特征数无关，仅由神经元数决定；
批处理维度：所有输出维度前加样本数 N N N，如批量隐藏状态维度为 ( N , n h ) (N, n_h) (N,nh)。

5.4 实战注意事项

数据预处理：股票收盘价需归一化（LSTM对数值敏感），时序数据需保持时间正序，不可打乱；
参数调整：神经元数 n h n_h nh 建议调整为16/32/64，学习率建议设为0.001~0.01，避免过大导致不收敛；
过拟合防控：股票样本有限，可加入Dropout层（如LSTM层后加Dropout(0.2)），减少过拟合。

六、附：股票预测LSTM核心代码（TensorFlow/Keras）

结合本文场景，提供单特征（收盘价）、单步回归预测的核心代码，标注关键参数和维度变化，可直接复用：

python 复制代码

import numpy as np
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout

# 1. 模拟股票收盘价数据（1000行，单特征），替换为真实数据
raw_data = np.random.rand(1000, 1)  # 原始收盘价，维度(1000,1)

# 2. 数据预处理（归一化+滑动窗口切分）
scaler = MinMaxScaler(feature_range=(0, 1))  # 归一化到[0,1]
data_scaled = scaler.fit_transform(raw_data)

timesteps = 10  # 时间步=10（10天输入）
X_train, y_train = [], []
# 滑动窗口切分：1000-10=990个样本
for i in range(timesteps, len(data_scaled)):
    X_train.append(data_scaled[i-timesteps:i, 0])  # 前10天收盘价（单特征）
    y_train.append(data_scaled[i, 0])              # 第11天收盘价（标签）

# 重塑为LSTM要求的三维输入格式：(samples, timesteps, features)
X_train = np.array(X_train)
y_train = np.array(y_train)
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))  # (990,10,1)

# 3. 搭建LSTM模型（LSTM+Dense）
model = Sequential()
# LSTM层：32个神经元，输入形状(10,1)，return_sequences=False（单步预测）
model.add(LSTM(units=32, input_shape=(timesteps, 1), return_sequences=False))
model.add(Dropout(0.2))  # 防止过拟合

# Dense层：1个神经元，回归预测（第11天收盘价）
model.add(Dense(units=1))

# 4. 编译模型（优化器Adam，损失函数MSE）
model.compile(optimizer='adam', loss='mean_squared_error')

# 5. 训练模型（epochs=50，batch_size=32，可调整）
model.fit(X_train, y_train, epochs=50, batch_size=32)

# 6. 预测示例（输入新的10天收盘价，预测第11天）
new_10_days = np.random.rand(1, 10, 1)  # 新的10天收盘价，维度(1,10,1)
pred_11th_day = model.predict(new_10_days)
# 反归一化，得到真实收盘价预测值
pred_11th_day = scaler.inverse_transform(pred_11th_day)
print("第11天收盘价预测值：", pred_11th_day[0][0])

附带一个LSTM的图