文章目录
- [1. 一维前缀和(DP34)](#1. 一维前缀和(DP34))
- [2. 二维前缀和(DP35)](#2. 二维前缀和(DP35))
- [3. 寻找数组的中心下标(LC724)](#3. 寻找数组的中心下标(LC724))
- [4. 除自身以外数组的乘积(LC238)](#4. 除自身以外数组的乘积(LC238))
- [5. 和为K的子数组(LC560)](#5. 和为K的子数组(LC560))
前缀和可以快速计算数组内某一连续区间的和,时间复杂度O(1),是简化版的动态规划
1. 一维前缀和(DP34)
题目描述

解题思路
- 预处理前缀和数组(
dp[])dp[i]表示从1到i所有元素的和,dp[i] = dp[i-1] + nums[i]
- 利用
dp[]数组返回结果[l,r]对应的和就是dp[r] - dp[l-1]
代码实现
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//读取数据
int n = in.nextInt();
int m = in.nextInt();
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++)
arr[i] = in.nextInt();
//主逻辑
long[] dp = new long[n + 1];
for(int i = 1;i <= n;i++)
dp[i] = dp[i-1]+arr[i];
for(int i = 0 ; i < m ; i++){
int l = in.nextInt();
int r = in.nextInt();
System.out.println(dp[r]-dp[l-1]);
}
}
}2. 二维前缀和(DP35)
题目描述

解题思路
- 预处理二维数组
dp[][]dp[i][j]表示arr[i][j]前所有元素之和。dp[i][j] = dp[i-1][j] + dp[i][j-1]+ arr[i][j] - dp[i-i][j-1]
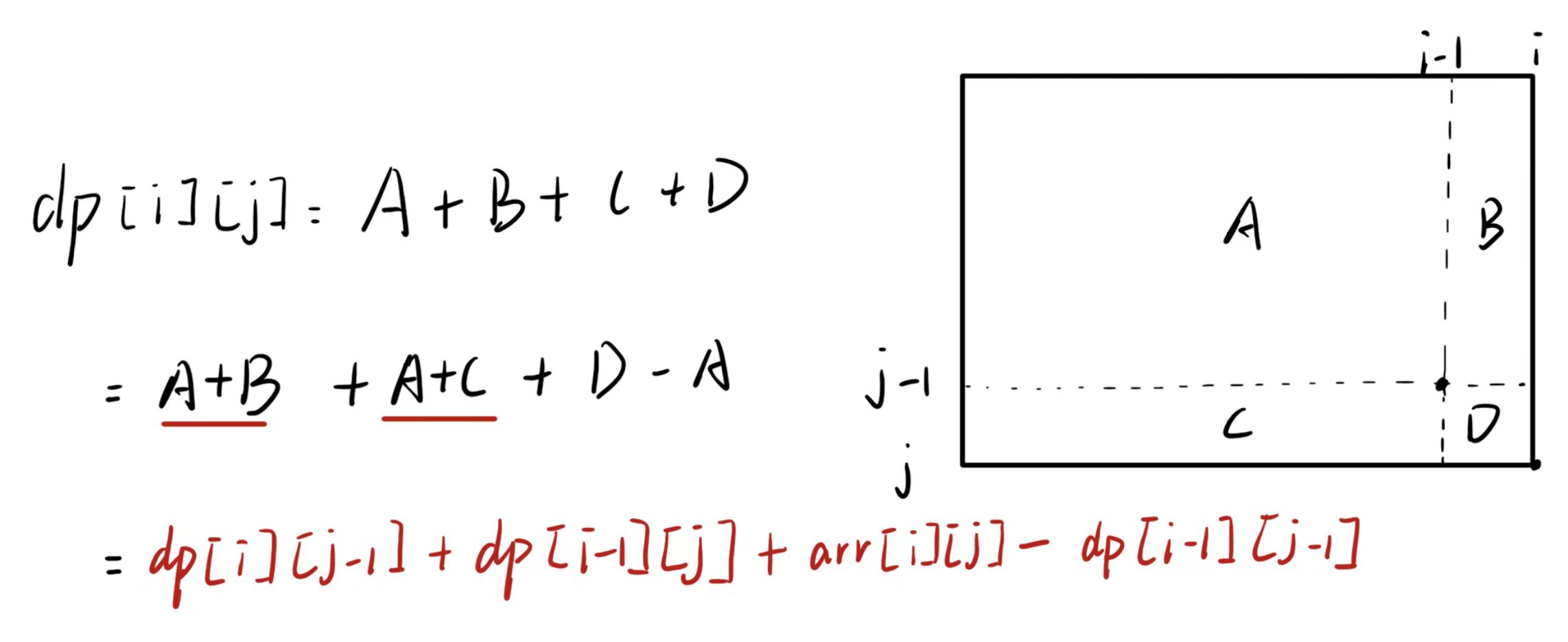
- 利用前缀和数组返回结果:(x1,y1)(x2,y2)之间元素之和为 dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 -1 ][y2] + dp[x1 - 1][y1 - 1]
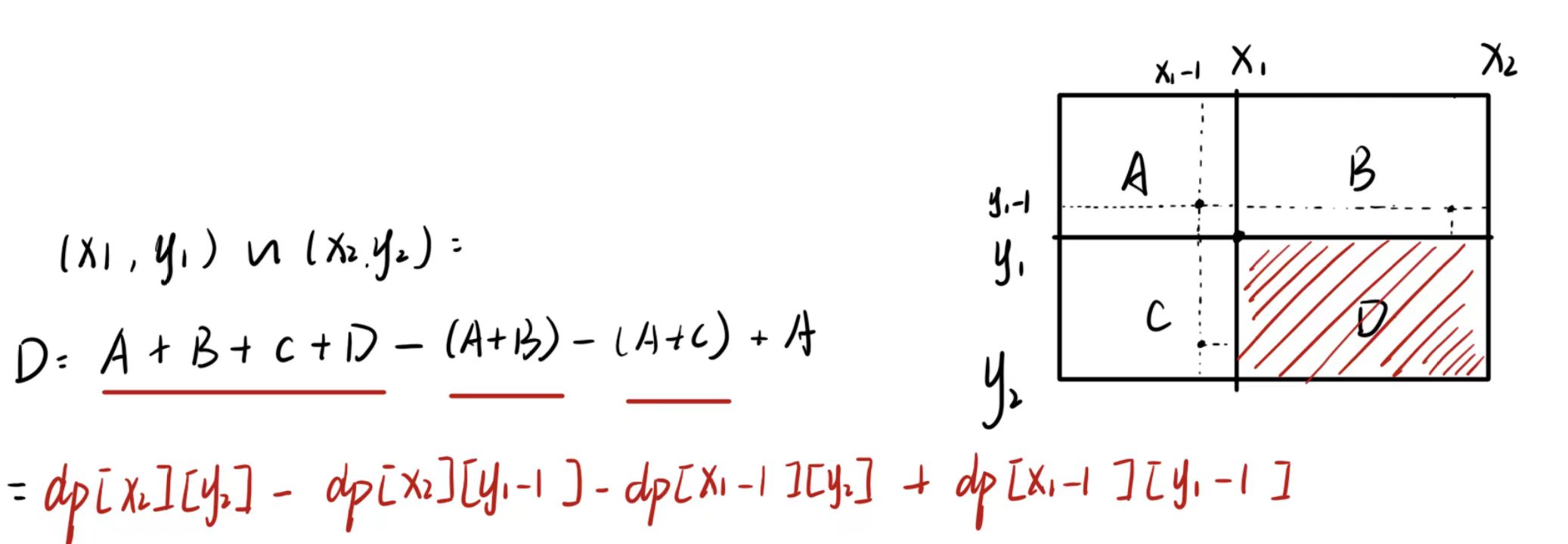
代码实现
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
//输入
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m = in.nextInt();
int q = in.nextInt();
int[][] arr = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++ ) {
for (int j = 1; j <= m; j++) {
arr[i][j] = in.nextInt();
}
}
//前缀和
long[][] dp = new long[n + 1][m + 1];
for (int i = 1; i <= n; i++ ) {
for (int j = 1; j <= m; j++) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j] + arr[i][j] - dp[i - 1][j - 1];
}
}
//查询
for(int i =0;i<q;i++){
int x1 = in.nextInt();
int y1 = in.nextInt();
int x2 = in.nextInt();
int y2 = in.nextInt();
long result = dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1];
System.out.println(result);
}
}
}3. 寻找数组的中心下标(LC724)
题目描述

解题思路
- 预处理两个数组:
f[i]表示i之前所有元素的和,不包括i。f[i] = f[i-1]+nums[i-1]g[i]表示i之后所有元素的和,不包括i。g[i] = g[i+1]+nums[i+1]
- 枚举所有中心下标,判断
f[i]==g[i]
注意:
- 初始化:为了防止越界,
f[0],g[0]要置为0,Java初始化的数组全部为0,这一步省略。 - 填表顺序:
f[i]从左向右;g[i]从右向左
代码实现
java
public int pivotIndex(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
for(int i = 1;i<n;i++)
f[i] = f[i-1] + nums[i-1];
for(int i = n - 2;i >= 0;i--)
g[i] = g[i+1] + nums[i+1];
for(int i = 0;i < n;i++)
if(f[i]==g[i])
return i;
return -1;
}4. 除自身以外数组的乘积(LC238)
题目描述

解题思路
- 与上题思想类似,把和改为乘积
f[i]表示i之前所有元素的积,不包括i。f[i] = f[i-1]*nums[i-1]g[i]表示i之后所有元素的积,不包括i。g[i] = g[i+1]*nums[i+1]
- 依次放入数组中,
ret[i] = f[i]*g[i]
注意: - 初始化:为了防止越界,
f[0],g[0]要手动置为1。 - 填表顺序:
f[i]从左向右;g[i]从右向左
代码实现
java
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
int[] ret = new int[n];
f[0] = g[n-1] = 1;
for(int i = 1;i < n;i++)
f[i] = f[i-1]*nums[i-1];
for(int i = n - 2;i >= 0;i--)
g[i] = g[i+1]*nums[i+1];
for(int i = 0;i<n;i++)
ret[i] = f[i]*g[i];
return ret;
}5. 和为K的子数组(LC560)
题目描述

解题思路
在以i为结尾的所有子数组中,找到和为K的子数组:
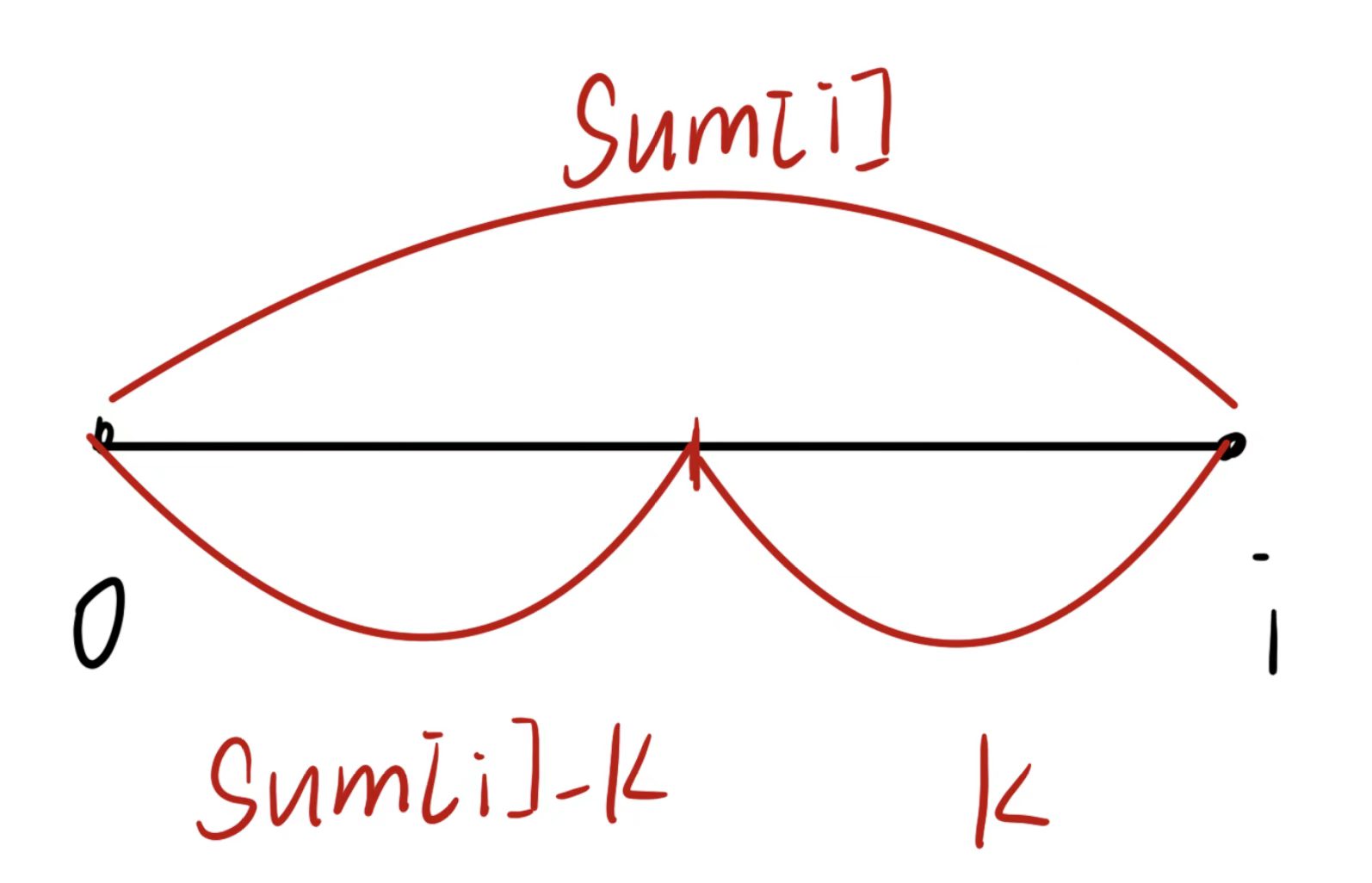
- 在
[0,i - 1]区间内,右区间和为K,那么左区间的和就是sum[i] - k. - 借助哈希表存储前缀和以及出现的次数,
细节问题:
- 前缀和加入哈希表的时机:不可以先计算所有的前缀和,再加入哈希表。结合以
i结尾的子数组思想,在计算i位置之前,哈希表应该存i之前的前缀和以及出现次数。 - 不需要创建前缀和数组,利用变量
sum来存储即可。 - 如果0到
i位置整个前缀和为K,会漏掉这种情况。需要把<0,1>存在哈希表中,表示前缀和为0出现了1一次。
注意: 这道题不可以用双指针来解,因为元素存在负数,不具有单调性,双指针可能漏掉结果。
代码实现
java
public int subarraySum(int[] nums, int k) {
int sum = 0;
int ret = 0;
HashMap<Integer,Integer> hash = new HashMap<>();
hash.put(0,1);
for(int x : nums){
sum += x;
//统计结果
ret += hash.getOrDefault(sum - k,0);
//把当前的sum放入hash表中
hash.put(sum,hash.getOrDefault(sum,0)+1);
}
return ret;
}