主旋参数定义
1.主旋轴(单位向量,3个参数) 和一个转动角度
2.主旋轴由一个方向单位向量构成,有3个参数,在N系和B系投影上有相同的分量。???
PRV与DCM的关系
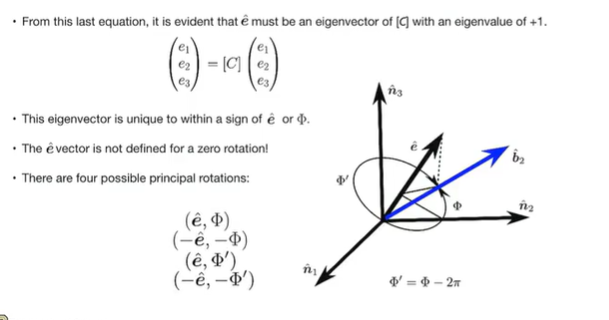
e 是C的特征向量,特征值为1

PRV特性
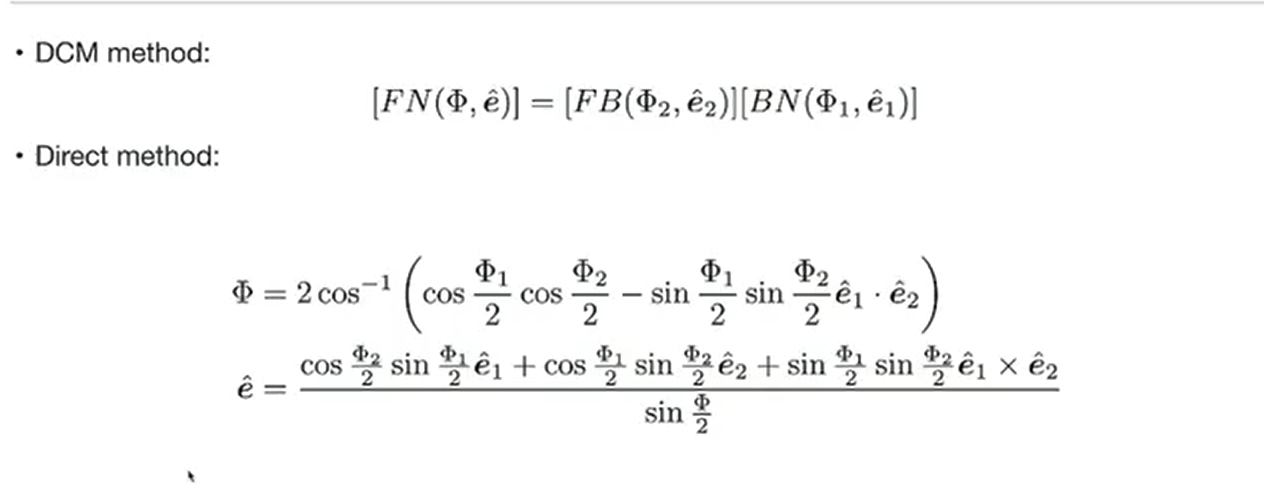
注意,分母 会存在奇点 0 180 °

主旋转参数
1 e 旋转轴
2 旋转角度
4组主旋转参数,从DCM到主旋转参数,有一个短角度有一个长角
(见上)
欧拉参数(四元数)的定义
四元数


将PRV映射到EP

EP 与DCM的关系
在这里插入图片描述

问题: β0 可能为0 ,会造成奇异点
用以下方法:

欧拉参数加法


微分运动学方程

很多人喜欢用四元数做线性估计



小节
- 定义与构成等价性:在姿态表示中,欧拉参数与单位四元数通常指代同一概念。坐标构成:由四个参数组成 β=[β0,β1,β2,β3]T\boldsymbol{\beta} = [\beta_0, \beta_1, \beta_2, \beta_3]^Tβ=[β0,β1,β2,β3]T。标量部分 (β0\beta_0β0):β0=cos(ϕ/2)\beta_0 = \cos(\phi/2)β0=cos(ϕ/2)。描述旋转的大小。矢量部分 (ϵ\boldsymbol{\epsilon}ϵ):β1,2,3=e^sin(ϕ/2)\beta_{1,2,3} = \hat{e} \sin(\phi/2)β1,2,3=e^sin(ϕ/2)。描述旋转轴及其分量。
- 重要特性非唯一性(双倍覆盖):同一姿态可以用 qqq 或 −q-q−q 表示。几何意义:一组代表优弧旋转(长路径),另一组代表劣弧旋转(短路径)。无奇异性:与欧拉角不同,四元数在任何姿态下都没有奇异点(不会出现死锁)。约束条件:必须满足单位范数约束:β02+β12+β22+β32=1\beta_0^2 + \beta_1^2 + \beta_2^2 + \beta_3^2 = 1β02+β12+β22+β32=13. 工程与控制应用归一化(Normalization):在数值积分(如 RK4 算法)过程中,由于舍入误差,四元数的模长会偏离 1。策略:通常在每个积分步结束时,手动将矢量除以其范数,使其重新回到超曲面上。
- 反绕问题(Unwinding Problem):如果控制律只驱动矢量部分 ϵ→0\boldsymbol{\epsilon} \to 0ϵ→0,而不检查 β0\beta_0β0 的正负,航天器可能会为了回到原点而多转一圈(走长路径)。解决方法:监测 β0\beta_0β0。若 β0<0\beta_0 < 0β0<0,则翻转所有参数符号以切换到短路径描述。
- 运动学方程微分方程:β˙=12[B(β)]ω\dot{\boldsymbol{\beta}} = \frac{1}{2} [B(\boldsymbol{\beta})] \boldsymbol{\omega}β˙=21[B(β)]ω。矩阵特性:通过在 3x1 矩阵前补 0 构造出的 4x4 矩阵具有正交性,便于数学求逆和变换。