我们这次来写几道经典的链表题目。
重排链表
题目描述
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → ... → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → ...
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
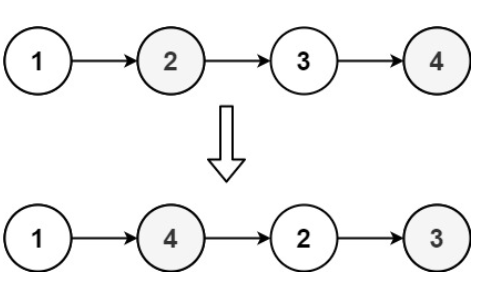
输入:head = [1,2,3,4]
输出:[1,4,2,3]
示例 2:
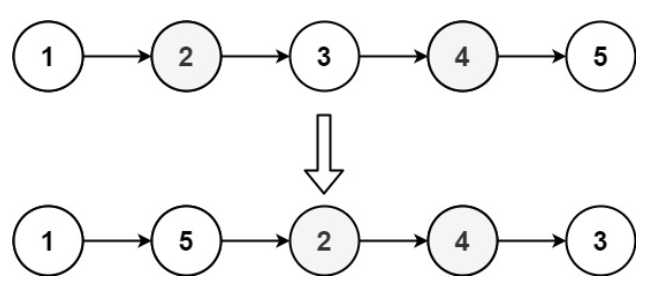
输入:head = [1,2,3,4,5]
输出:[1,5,2,4,3]
提示:
- 链表的长度范围为 [1, 5 * 104]
- 1 <= node.val <= 1000
算法原理
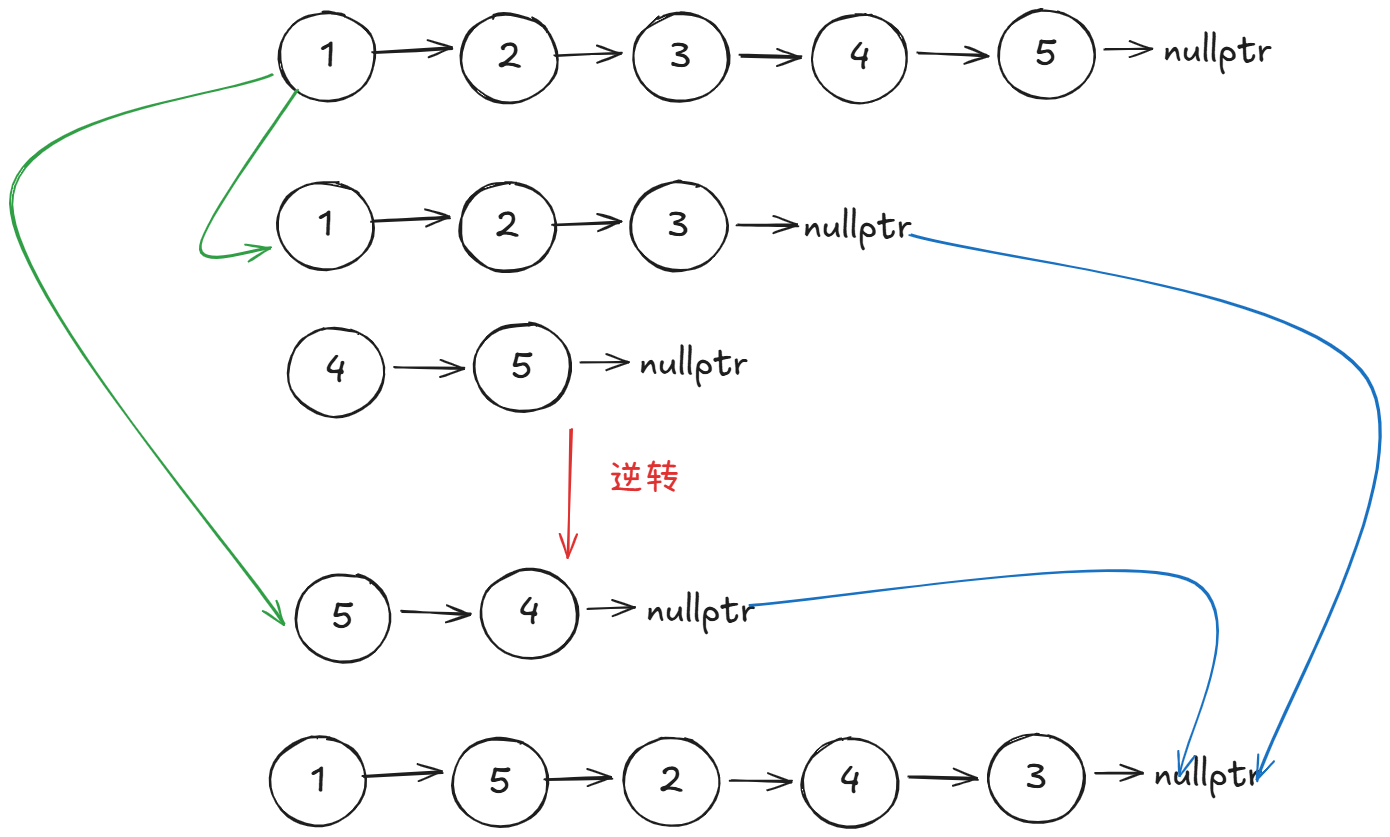
根据题目描述,我们实际上是如此插入:
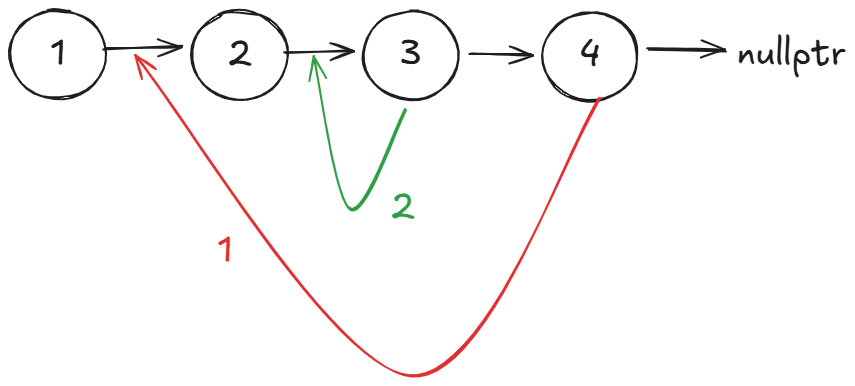
实际上我们是将后半部分,逆序插入前半部分中:
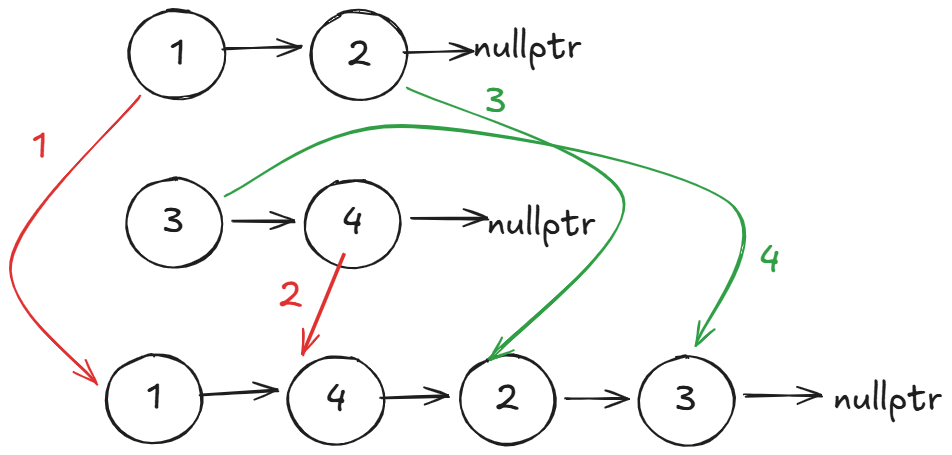
- 那么我们实际上可以先将链表从中间断开,然后逆序后半部分,最后合并即可。
- 首先我们要找到断开的位置,我们考虑奇数情况和偶数情况,偶数情况如上,奇数如下:
不难发现,我们要断开的结点就是最中间结点,或者中间左边结点。
那么我们考虑使用这样的快慢指针:
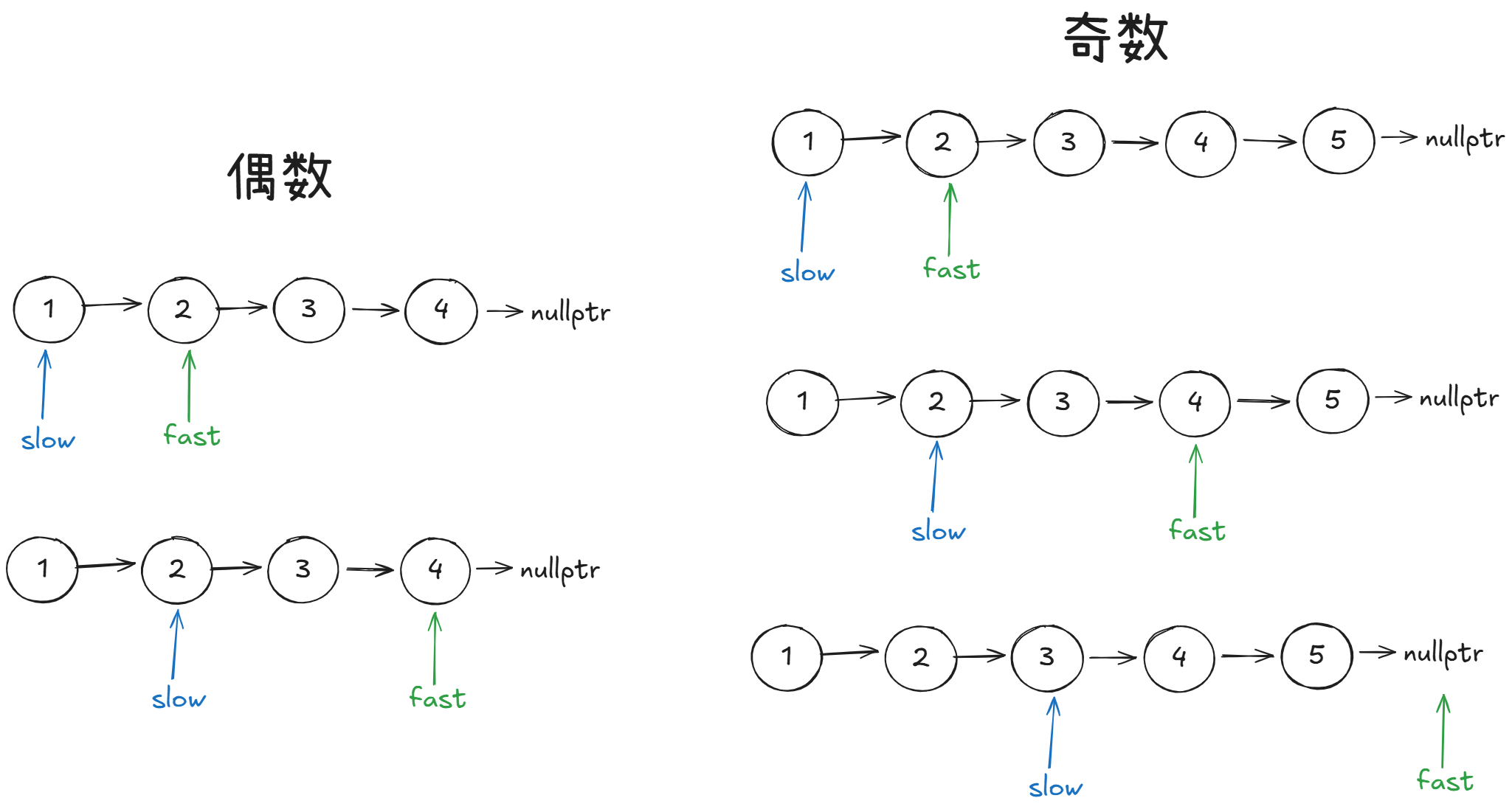
fast直接从头结点的下一个结点出发,最后fast为空或者fast->next为空终止。
这样slow指向正是我们要断开的地方。
- 然后我们要逆序后半部分,这显然是非常简单的。这里考虑头插法逆序:
我们先创建一个哨兵位头结点:
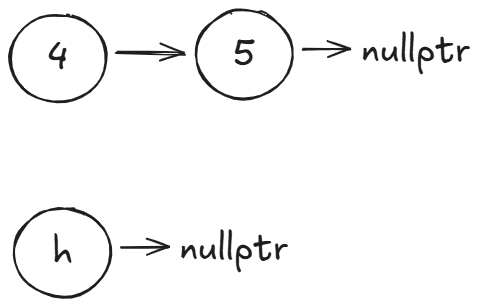
然后将上面的链表逐个头插到下面:
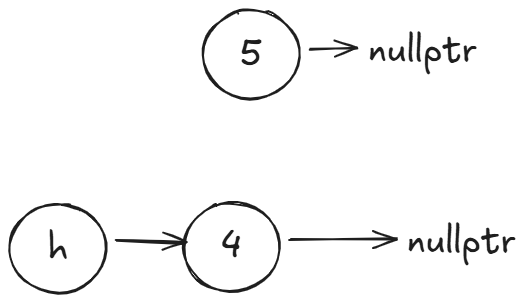

最后将头结点释放即可。
- 合并
合并这个太简单了,参考归并
我们遍历两个链表,顺序尾插到一个新的头结点后即可。当然也可以原地插入。
算法实现
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
void reorderList(ListNode* head) {
if(!head || !head->next)return;
//找中点
ListNode *slow = head, *fast = head->next;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
}
fast = slow->next;
slow->next = nullptr;//断开两链表
slow=head;
//逆序后半部分
ListNode *newhead =new ListNode, *cur = fast, *next;
while(cur){
next = cur->next;
cur->next = newhead->next;
newhead->next = cur;
cur = next;
}
fast = newhead->next;
delete newhead;
//合并两链表
ListNode *next1, *next2;
while(fast){
next1=slow->next;
next2=fast->next;
slow->next=fast;
fast->next=next1;
slow=next1;
fast=next2;
}
}
};
合并 K 个升序链表
题目描述
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
1-\>4-\>5, 1-\>3-\>4, 2-\>6
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
- k == lists.length
- 0 <= k <= 10^4
- 0 <= lists[i].length <= 500
- -10^4 <= lists[i][j] <= 10^4
- lists[i] 按 升序 排列
- lists[i].length 的总和不超过 10^4
算法原理
- 堆
我们可以维护一个大小为k的小根堆,每次从堆顶获取结点插入到新头结点中。
然后插入头结点的next结点,除非为空。
直到堆为空终止。
那么时间复杂度就是O(nklogk)。其中nk是节点元素个数,logk是堆调整的开销。
- 分治
我们可以将k个链表分成一半,分别合并这两半,最后再合并再一起。
参考归并的思想。
算法实现
堆
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
struct cmp {
bool operator()(const ListNode* l, const ListNode* r) {
return l->val > r->val;
}
};
ListNode* mergeKLists(vector<ListNode*>& lists) {
priority_queue<ListNode*, vector<ListNode*>, cmp> heap;
for (auto& e : lists)
if(e)heap.push(e);
ListNode *head = new ListNode, *tail = head;
while (heap.size()) {
ListNode* temp = heap.top();
heap.pop();
if (temp->next)
heap.push(temp->next);
tail->next = temp;
temp->next = nullptr;
tail = temp;
}
tail = head->next;
delete head;
return tail;
}
};分治
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
ListNode* merge(vector<ListNode*>& lists, int left, int right) {
if (left > right)
return nullptr;
if (left == right)
return lists[left];
int mid = left + (right - left) / 2;
ListNode* list1 = merge(lists, left, mid);
ListNode* list2 = merge(lists, mid + 1, right);
ListNode *head = new ListNode, *tail = head;
while (list1 && list2) {
if (list1->val < list2->val) {
tail->next = list1;
list1 = list1->next;
tail = tail->next;
tail->next = nullptr;
} else {
tail->next = list2;
list2 = list2->next;
tail = tail->next;
tail->next = nullptr;
}
}
list1 = list1 ? list1 : list2;
while (list1) {
tail->next = list1;
list1 = list1->next;
tail = tail->next;
tail->next = nullptr;
}
tail = head->next;
delete head;
return tail;
}
};K 个一组翻转链表
题目描述
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
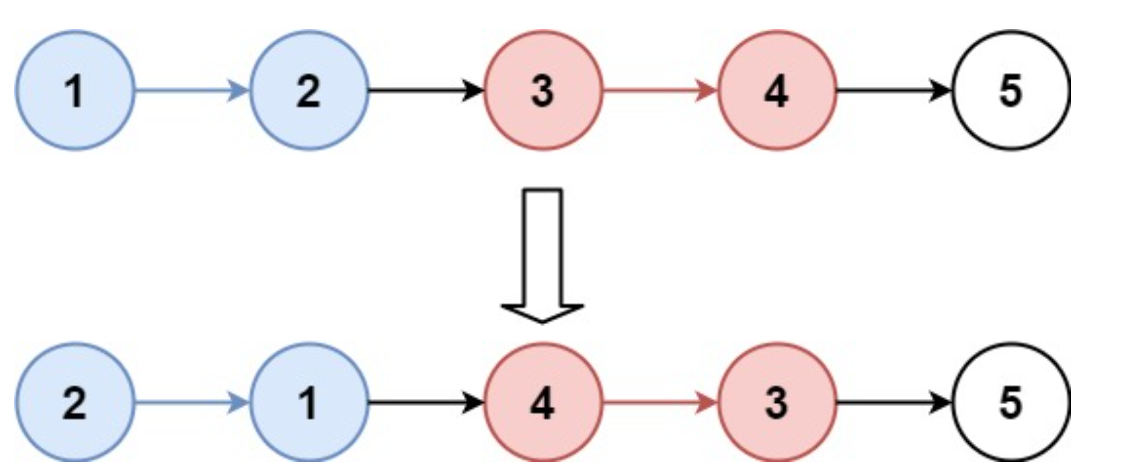
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
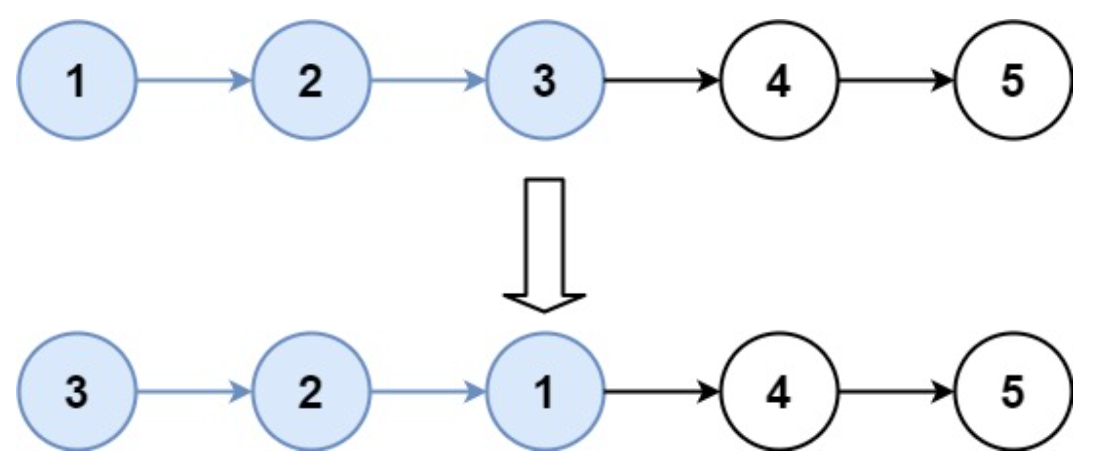
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
提示:
链表中的节点数目为 n
- 1 <= k <= n <= 5000
- 0 <= Node.val <= 1000
进阶:你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗?
算法原理
- 递归
我们之间将前k个结点翻转,然后剩下部分交给递归解决即可。不过这样的空间开销比较大,也可以换成迭代方式实现。迭代的话要先求出翻转的次数。
算法实现
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if(!head)return head;
ListNode* tail = head;
int n = k - 1;
while (n--) {
if (!tail || !tail->next)
return head;
tail = tail->next;
}
ListNode* next = reverseKGroup(tail->next, k);
tail->next = nullptr;
reverse(head);
head->next = next;
return tail;
}
void reverse(ListNode* head) {
ListNode *newhead = new ListNode, *next;
while (head) {
next = head->next;
head->next = newhead->next;
newhead->next = head;
head = next;
}
delete newhead;
}
};