循环队列+双端队列（C语言）

文章目录

队列
双端队列

队列

理论

只允许在一端就进行插入，另一端进行删除放入线性表，没有查找和修改操作

类似于排队，有队首和队尾

队首：执行插入

队尾：执行删除

特殊：空队列:不含任何元素

性质：先进先出

指针只是类比

队头"指针"int

队尾"指针"int

1.队列的顺序存储：顺序队列--数组maxx（数组队头到队尾部分是队列）

队首指针：int f= 0;

队尾指针：int r

（1）队尾指针r指向真正的队尾元素

真正的队尾元素初始化（没有元素可以指向）r=-1
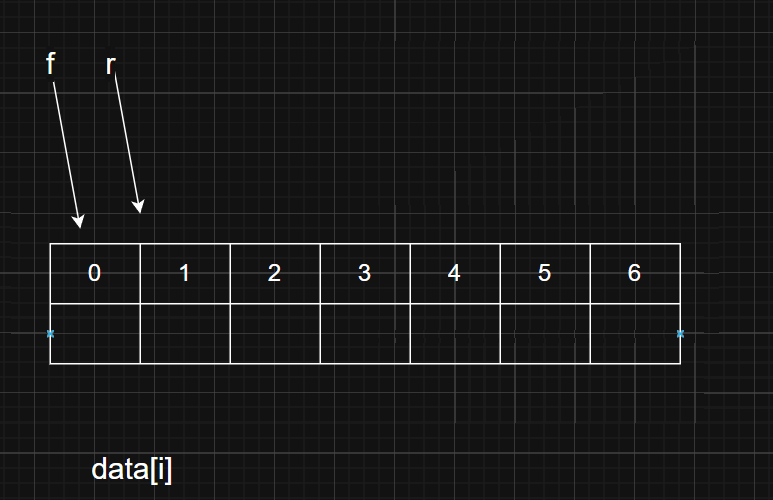
入队:data[++r]=k;
出队:改变首指针的位置:++f;
判满：判断数组能否还能容纳数据，r==maxx-1( 存在假满的情况)假溢出

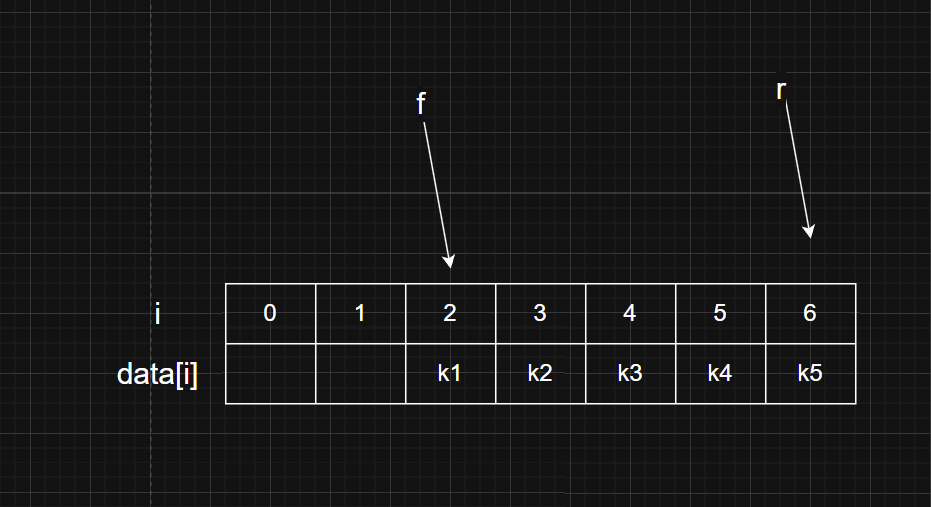
判断空f==r+1

（2）队尾指针r指向真正的队尾元素的下一个位置（要插入的位置），r-1是真正的队尾

初始化：f=0 r=0
入队: data[r]=k,r++. //data[r++]=k
出队：删除队首指针指向的数据。f++
判满：判数组还能否容纳数据。 r == maxx（可能存在假满）. 假溢出-----循环队列（下面提及）

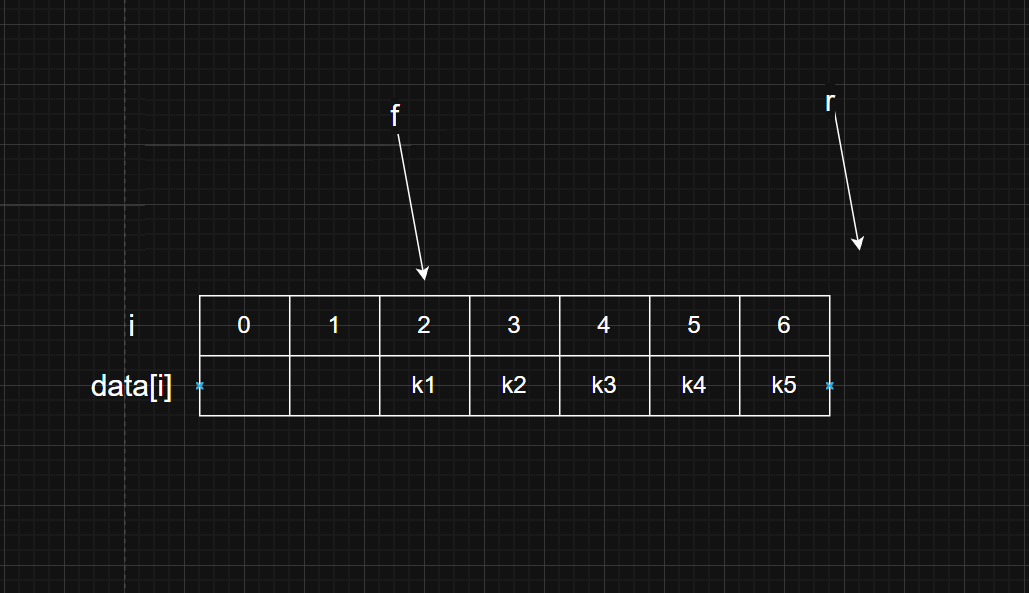
判空:f==r

循环队列：基于循环数组实际上为普通的数组只不过用数学方法实现了下标的首尾相接（r指向真正的队尾元素的下一个位置 ------写法**（2）**）

初始化:f=0 r=0
入队: data[r]=k,r=(r+1)%maxx
出队：删除队首指针指向的数据。
判满：判断数组还能否容纳数据

(1)可以通过记录数据个数,维护麻烦

(2)引入标注变量满之前的操作一定是入队

flag==0 出队 flag==1 入队

r==f&&flag==1 满。

r==f&&flag==0 空

但是维护麻烦

(3)牺牲一个空间(常用)这个空间不一定是maxx-1

判空：f==r
满：f==(r+1)%maxx

2.队列的链式存储：链式队列---带头节点的单链表

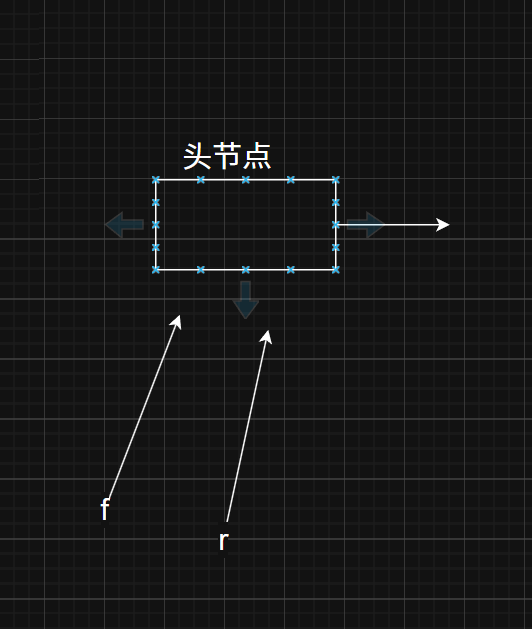
首元节点队首

尾节点队尾

头指针做队首指针 （队首指针指向真正队首的上一个节点）

队尾指针：指向为节点的尾指针

初始化：创建头节点，队首指针和队尾指针指向头节点
入队：尾节点后面插入
出队：删除首元节点
判空：队首指针和队尾指针指向同一个节点（头节点），f==r或者L->next==NULL

不存在假溢出不用循环

代码

顺序存储--循环队列

c 复制代码

#include<stdio.h>
#include<stdlib.h>
#define MAXX 10

//循环队列
typedef struct {
	int* data;
	int front;
	int rear;
}QueueCircle;

// 创建并初始化
QueueCircle* initQueue( ) {
	QueueCircle* q = malloc(  sizeof(QueueCircle));
	if (q == NULL) {
		printf("分配空间失败\n");
		return NULL;
	}

	q->data = malloc(MAXX * sizeof(int));
	if (q->data == NULL) {
		printf("分配空间失败\n");
		free(q);
		return NULL;
	}

	q->front = q->rear = 0;
	return q;
}


//保证q存在
//入队
// f,r指向元素的下一个位置
void EnQueue(QueueCircle* q,int k) {
	if (q->front == (q->rear + 1) % MAXX)
	{
		//留一个位置不装元素区别 满和空
		printf("队列满，无法入队\n");
		return;
	}
	printf("%d入队\n", k);
	q->data[q->rear] = k;
	q->rear = (q->rear + 1) % MAXX;
}

static int isEmple(QueueCircle* q) {
	return q->front == q->rear;
}

static int Getfront(QueueCircle* q) {
	return q->data[q->front];
}

//保证q存在
//出队
// f,r指向元素的下一个位置
void DeQueue(QueueCircle* q ) {
	if (isEmple(q)) {
		printf("队列空，无法出队\n");
		return;
	}
	printf("%d出队\n", Getfront(q));
	 
	q->front = (q->front + 1) % MAXX;
}

int main() {

	QueueCircle* queue = initQueue();
	EnQueue(queue, 1);
	EnQueue(queue, 2);
	EnQueue(queue, 3);

	DeQueue(queue);
	DeQueue(queue);
	DeQueue(queue);

	DeQueue(queue);

	EnQueue(queue, 1);
	EnQueue(queue, 2);
	EnQueue(queue, 3);

	return 0;
}

链式队列

c 复制代码

#include<stdio.h>
#include<stdlib.h>


//链队
//节点结构
typedef struct Node {
	int  data;
	struct Node* next;
}LinkQueueNode;

//队列结构
typedef struct {
	LinkQueueNode* front;//头指针
	LinkQueueNode* rear;//尾指针
}LinkQueue;


// 创建并初始化
LinkQueue* initQueueL() {
	//1.队列结构
	LinkQueue* q = malloc(sizeof(LinkQueue));
	if (q == NULL) {
		printf("分配空间失败\n");
		return NULL;
	}


	//2.头节点
	LinkQueueNode* L = malloc(sizeof(LinkQueueNode));
	if (L == NULL) {
		printf("分配空间失败\n");
		free(q);
		return NULL;
	}
	L->next = NULL;

	//均指向头节点
	q->rear = q->front=L;
	
	//q->front->data//脏数据
	 

	return q;
}


//保证q存在
//入队
//  
void EnQueueL(LinkQueue* q, int k) {

	LinkQueueNode* p = malloc(sizeof(LinkQueueNode));
	if (p == NULL) {
		printf("分配空间失败\n");
		return;
	}
	p->data = k;
	p->next = NULL;

	//队尾入队
	p->next = q->rear->next;
	q->rear->next = p;

	q->rear = p;
	q->rear->data = p->data;
	printf("%d入队\n", q->rear->data);

}

static int isEmpleL(LinkQueue* q) {
	if (q->front->next == NULL)
		return 1;
	return 0;
}


//保证不为空
//得到队头元素
static int GetfrontL(LinkQueue* q) {
	 
	return q->front->next->data;
	 
 
}

//保证q存在
//出队
// f指向元素的上一个位置
void DeQueueL(LinkQueue* q) {
	if (isEmpleL(q)) {
		printf("队列空，无法出队\n");
		return;
	}


	printf("%d出队\n", GetfrontL(q));
	LinkQueueNode* tFree = q->front->next;
	q->front->next = tFree->next;

	if (tFree == q->rear) {
		//防止尾指针成为野指针
		q->rear = q->front;
	}
	free(tFree);
	tFree = NULL;

}

int main() {

	LinkQueue* queue = initQueueL();
	EnQueueL(queue, 1);
	EnQueueL(queue, 2);
	EnQueueL(queue, 3);

	DeQueueL(queue);
	DeQueueL(queue);
	DeQueueL(queue);

	DeQueueL(queue);

	EnQueueL(queue, 1);
	EnQueueL(queue, 2);

	DeQueueL(queue);
	DeQueueL(queue);
	DeQueueL(queue);
	return 0;
}

应用

一些需要排队的需求

解决主机与外部设备速度不匹配

多用户引起的资源竞争问题

双端队列

理论

概念

两端均允许入队操作和出队操作，依旧没有查找和修改操作。灵活

不分队首和队尾

通过四种操作可以搞一些特殊操作

左边进左边出右边进右边出 共用底的栈

左右进只有一边出 栈和队列混合体

考研题

有一个双端队列，规定两端均允许入队，只有一端允许出队 。按照abcde的顺序依次入队，最后连续出队，以下哪个出队序列不合法？C

A: bacde

B: ecbad

C: dbcae

最终出队的顺序就是数据在队列里面的顺序

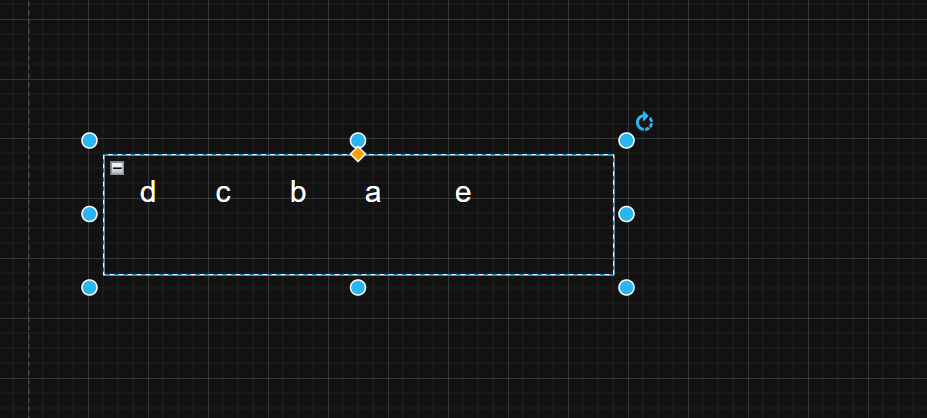
初始化左端入队左端出队右端入队右端出队判满判空

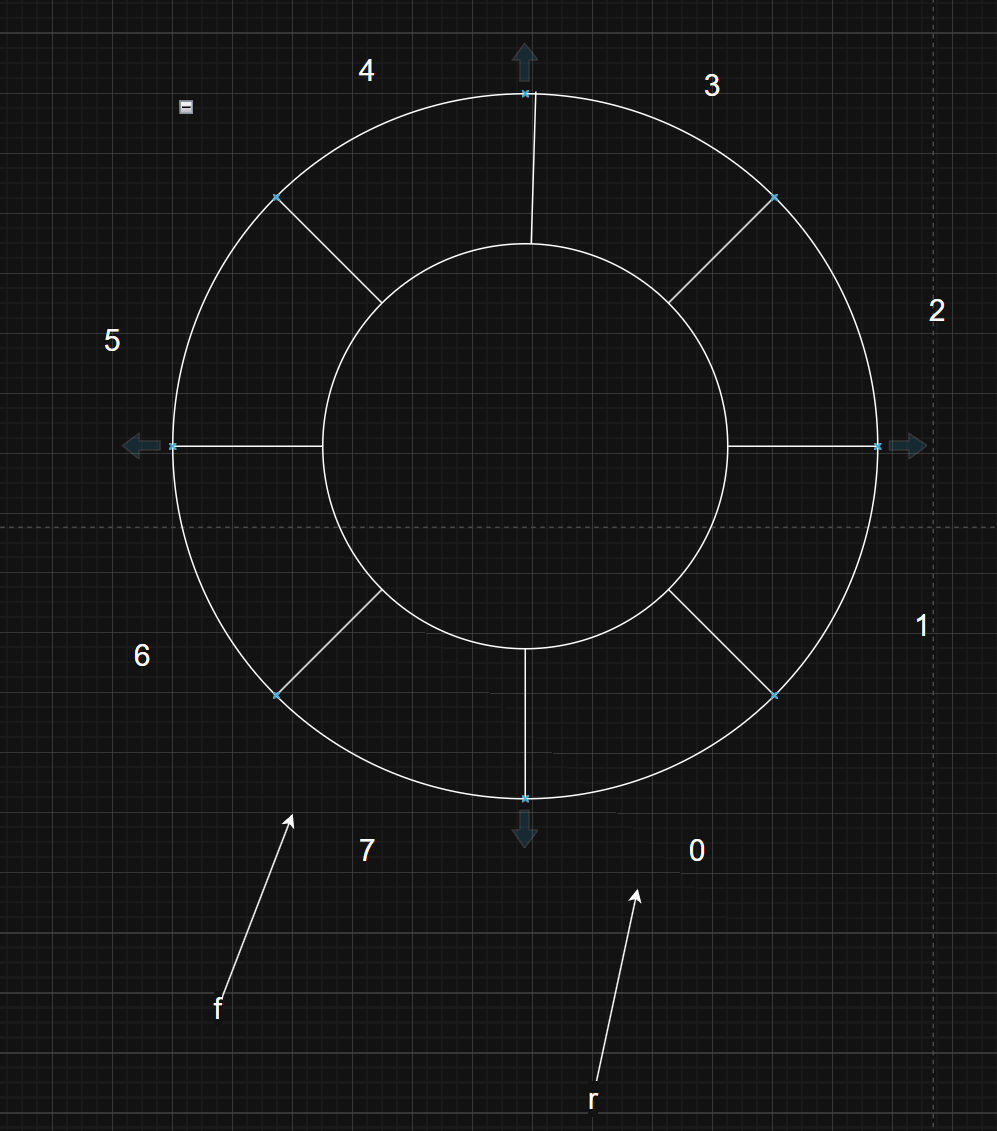
基于顺序存储结构 的双端队列--循环数组 左端"指针"右端"指针"

循环数组可以有效地利用数组空间。在普通数组中，如果我们在队列的一端进行插入和删除，可能会导致数组的一端空闲而另一端已满。

基于链式存储结构 的双端队列--双向链表

操作

顺序存储结构

初始化：I=0 r=0
左端入队：数据k左端入队
- 1如果认为 I指向真正的左端数据 I=(l-1 +maxx)%maxx. data[l]=k;
- 2如果认为 I指向真正的左端数据前一个位置 data[l]=k，I=(l-1+maxx)%maxx
右端入队：数据k右端入队
- 3如果认为 r指向真正的左端数据r=(r-1 +maxx)%maxx. data[l]=k;
- 4如果认为 r指向真正的左端数据前一个位置 data[l]=k，r=(r-1+maxx)%maxx
- 左右搭配组合 14 23正确
- 如果13 会覆盖掉 24会有空位置
左端出队:I=(l+1)%maxx
右端出队:r= (r-1+maxx） %maxx（只要可能为负数就要加）
判满判空:

引入一个变量sum记录队列中数据的个数
- if(sum==0)空
- if(sum==maxx)满

链式存储结构

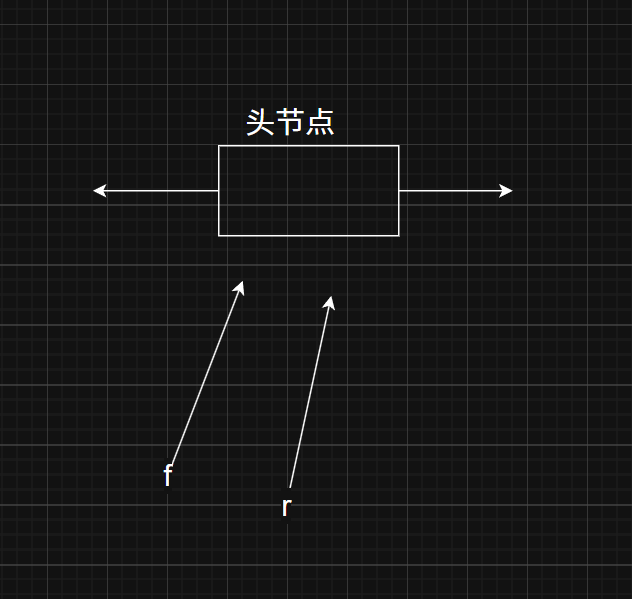
类似于前者，也有两种入队出队

初始化：创建一个带头结点的空的双向链表，l r都指向头结点

l认为指向真正的左端数据，如果认为r指向真正的右端数据后一个位置 （头节点放数据，最后一个节点为脏数据）
左端入队：新建一个结点s ，s->data=k,s插入到I的前边,
右端入队：r->data=k,新建一个结点s ,s插入到r后边，此时s中是脏数据，s的上一个节点才是真正的右端数据
左端出队：把l指向的结点free
右端出队：把r指向的结点free

代码

顺序存储

c 复制代码

#include<stdio.h>
#include<stdlib.h>

#define maxx 5

// 双端队列结构体
// 认为 l 指向真正的左端数据，r 指向真正的右端数据的后一个位置
typedef struct {
    int* data;   // 数组，存放数据
    int l, r;    // 左端和右端指针
    int sum;     // 队列中数据的个数
} Deque;

// 初始化双端队列
Deque InitDeque() {
    Deque q;
    q.data = (int*)malloc(sizeof(int) * maxx);
    // if(q.data == NULL) // 可以添加内存分配失败检查
    q.l = q.r = 0;
    q.sum = 0;
    return q;
}

// 左端入队
void LInsert(Deque* q, int k) {
    if (q->sum == maxx) {
        printf("队满，无法入队");
    } else {
        q->l = (q->l - 1 + maxx) % maxx;
        q->data[q->l] = k;
        q->sum++;
    }
}

// 右端入队
void RInsert(Deque* q, int k) {
    if (q->sum == maxx) {
        printf("队满，无法入队");
    } else {
        q->data[q->r] = k;
        q->r = (q->r + 1) % maxx;
        q->sum++;
    }
}

// 左端出队
void LDelete(Deque* q) {
    if (q->sum == 0) {
        printf("队空，无法出队");
    } else {
        printf("%d左端出队\n", q->data[q->l]);
        q->l = (q->l + 1) % maxx;
        q->sum--;
    }
}

// 右端出队
void RDelete(Deque* q) {
    if (q->sum == 0) {
        printf("队空，无法出队");
    } else {
        q->r = (q->r - 1 + maxx) % maxx;
        printf("%d右端出队\n", q->data[q->r]);
        q->sum--;
    }
}

int main() {
    Deque q = InitDeque();
    
    LInsert(&q, 1);
    LInsert(&q, 2);
    LInsert(&q, 3);
    
    RInsert(&q, 6);
    RInsert(&q, 7);
    
    RDelete(&q);
    RDelete(&q);
    RDelete(&q);
    
    LDelete(&q);
    LDelete(&q);
    LDelete(&q);
    
    return 0;
}

链式存储

头节点也放数据

c 复制代码

#include <stdio.h>
#include <stdlib.h>

// 链表结点结构
typedef struct Node {
    int data;
    struct Node* next;
    struct Node* pre;
} Node;

typedef struct {
    Node* l;  // 左端指针
    Node* r;  // 右端指针
} Deque;

// 初始化双端队列
Deque InitDeque() {
    Deque q;
    // 创建一个链表的头结点
    Node* s = (Node*)malloc(sizeof(Node));
    // if(s==NULL) // 实际使用中应该检查malloc是否成功
    s->next = s->pre = NULL;
    q.l = q.r = s;
    return q;
}

// 左端入队
void LInsert(Deque* q, int k) {
    // 创建一个结点s
    Node* s = (Node*)malloc(sizeof(Node));
    // if(s==NULL) // 实际使用中应该检查malloc是否成功
    s->data = k;
    q->l->pre = s;
    s->next = q->l;
    s->pre = NULL;
    q->l = s;
}

// 右端入队
void RInsert(Deque* q, int k) {
    // 创建一个结点s
    Node* s = (Node*)malloc(sizeof(Node));
    // if(s==NULL) // 实际使用中应该检查malloc是否成功
    
    
    // 将数据放入当前右指针指向的节点
    q->r->data = k;
    
    // 设置新节点的前后关系
    s->pre = q->r;
    s->next = NULL;
    q->r->next = s;
    
    // 更新右指针指向新节点
    q->r = s;
}

// 左端出队
void LDelete(Deque* q) {
    if (q->l == q->r) {
        printf("队空,无法出队\n");
    } else {
        Node* p = q->l;
        printf("%d左端出队\n", p->data);
        q->l = q->l->next;
        q->l->pre = NULL;
        free(p);
        p = NULL;
    }
}

// 右端出队
void RDelete(Deque* q) {
    if (q->l == q->r) {
        printf("队空,无法出队\n");
    } else {
        Node* p = q->r;
        // 注意：这里输出的是r的前一个节点的数据
        printf("%d右端出队\n", p->pre->data);
        q->r = q->r->pre;
        q->r->next = NULL;
        free(p);
        p = NULL;
    }
}

int main() {
    Deque q = InitDeque();
    LInsert(&q, 1);
    LInsert(&q, 2);
    LInsert(&q, 3);
    RInsert(&q, 6);
    RInsert(&q, 7);
    RDelete(&q);
    RDelete(&q);
    RDelete(&q);
    LDelete(&q);
    LDelete(&q);
    LDelete(&q);
    return 0;
}

头节点不放数据版本

c 复制代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

//节点结构
typedef struct nodeL {
	int data;
	struct nodeL* next;
	struct nodeL* pre;
}Node;
//双端队列链式结构
typedef struct {
	Node* L;
	Node* l;
	Node* r;
}LDeque;


LDeque* initLDeque() {
	//1.初始化队列
	LDeque* q = malloc(sizeof(LDeque));
	if (q == NULL) {
		printf("内存分配失败\n");
		return NULL;
	}
	q->l = q->r = NULL;

	//2.初始化头节点
	Node* L=malloc(sizeof(Node));
	if (L == NULL) {
		printf("内存分配失败\n");
		return NULL;
	}
	//除了节点的数据域不用管
	L->next = L->pre = NULL;
	q->L = L;
	q->l = q->r = L;
	return q;
}

//假设q存在
void LInsert(LDeque* q, int k) {
	//1.创建节点
	Node* s = malloc(sizeof(Node));
	if (s == NULL) {
		printf("内存分配失败\n");
		return  ;
	}

	s->data = k;
	
	//2.插入
	s->pre = q->l->pre;
	q->l->pre = s;
	s->next = q->l;

	
	//3.更新l指针
	q->l = s;

	printf("%d左入队\n", q->l->data);
}

//假设q存在
void RInsert(LDeque* q, int k) {
	//1.创建节点
	Node* s = malloc(sizeof(Node));
	if (s == NULL) {
		printf("内存分配失败\n");
		return  ;
	}

	s->data = k;
	//2.插入
	s->next = q->r->next;
	s->pre = q->r;
	q->r->next = s;
	

	//3.更新l指针
	q->r = s;

	printf("%d右入队\n", q->r->data);

}


void Lfree(LDeque* q) {
	//1.判断空
	if (q->l == q->r&&q->l==q->L) {
		printf("队空无法出队\n");
		return;
	}

	Node* temp = NULL;
	//1.5左边没有节点了 开始出队头节点右边的数据 删除首元节点
	//如果右边只有一个节点还要维护指针r
	if (q->l == q->L) {
		 temp = q->L->next;//头节点的下一个删除的节点
		q->L->next = temp->next;
		if(temp->next)
		{
			temp->next->pre = q->L;
		}
		//free(temp);
		if (temp== q->r) {
			q->r = q->L;
		}
	}

	else{
	//2.连接
	  temp =q-> l;
	//3.更新指针
	q->l = temp->next;
	temp->next->pre = NULL;
	/*printf("%d左出队\n", temp->data);
	free(temp);*/
	}

	printf("%d左出队\n", temp->data);
	free(temp);
}

void Rfree(LDeque* q) {
	//1.判断空
	if (q->l == q->r && q->l == q->L) {
		printf("队空无法出队\n");
		return;
	}
	Node* temp = NULL;//要删除的节点

	//1.5右边数据不够出队但是左边还有就开始删除头节点前驱节点
	//注意维护l指针
	if (q->r == q->L) {
		temp= q->L->pre;
		q->L->pre = temp->pre;
		if (temp->pre) {
			temp->pre->next = q->L;
		}
		if (temp == q->l) {
			q->l = q->L;
		}

	}
	else {
		//2.连接并释放 3.更新指针
		 temp = q->r;
		q->r = temp->pre;
		temp->pre->next = NULL;//后面一定是空
	}
	
	printf("%d右出队\n", temp->data);
	free(temp);
}


int main() {
	LDeque* q = initLDeque();
	LInsert(q, 1);
	RInsert(q, 2);
	RInsert(q, 3);

	Rfree(q);
	Lfree(q);
	Lfree(q);
	Lfree(q);
	Lfree(q);

	LInsert(q, 1);
	LInsert(q, 2);
	LInsert(q, 3);

	Rfree(q);
	Rfree(q);
	Rfree(q);
	Rfree(q);

	return 0;
}