【C语言】浮点型（实型）变量

介绍

浮点型（Floating Point Type）是C语言中用于表示实数的数据类型。实数包括整数、小数以及科学计数法表示的数，例如：

3.14
1.23e-2（即 1.23×10−21.23×10^{−2}1.23×10−2）
4.56e+5（即 4.56×10+54.56×10^{+5}4.56×10+5）

浮点数之所以称为"浮点"，是因为其小数点的位置是可变的，通过指数部分来调节，从而能够表示极大或极小的数值。

浮点型关键字

C语言中常用的浮点型关键字有两种：

类型	关键字	字节数	有效位数（约）	格式控制符
单精度	`float`	4 Byte	6~7 位十进制	`%f`
双精度	`double`	8 Byte	15~16 位十进制	`%lf`（输入） / `%f`（输出）

注意：

由于实数集合是无限的，而计算机内存有限，因此并非所有实数都能精确表示，部分数值只能存储其近似值。
此外，C99标准还引入了 long double 类型，通常为10字节或更多，提供更高精度。

浮点型在内存中的存储原理

浮点数在内存中通常采用IEEE 754标准存储，其结构分为三部分：

符号位（Sign）：表示正负
指数位（Exponent）：表示科学计数法中的指数（带偏移）
尾数位（Mantissa/Fraction）：表示有效数字的小数部分

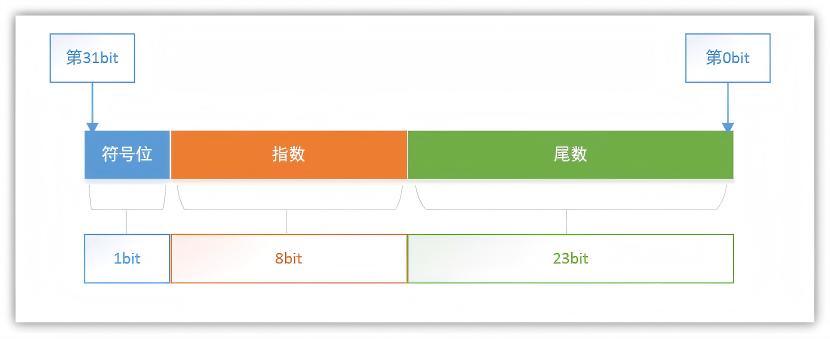
单精度（float）存储格式（32位）：

1位符号位
8位指数位（偏移量 +127）
23位尾数位

双精度（double）存储格式（64位）：

1位符号位
11位指数位（偏移量 +1023）
52位尾数位

对于浮点数的规范目前大部分系统都采用的是IEEE 754标准。这里以4字节单精度浮点类型为例子讲解一下浮点数的存储形式（其他浮点数存储仅仅每部分数据大小不同）：

这里以float型浮点数:4.25为例子，如下转化示意图：

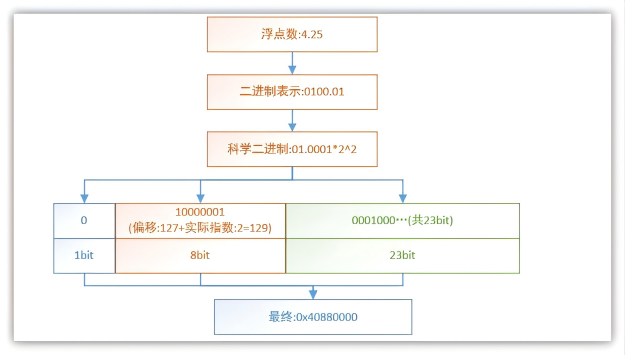
转为二进制：100.01
科学计数法：1.0001×221.0001×2^21.0001×22
符号位：0（正）
指数：2 + 127 = 129 → 二进制 10000001
尾数：00010000000000000000000（取小数点后部分，补齐23位）
最终内存表示（十六进制）：0x40880000

输入输出与格式控制符

操作	单精度（float）	双精度（double）
输入	`%f`	`%lf`
输出	`%f`	`%f`

控制输出精度与宽度

%m.nf：输出总宽度为 m，其中小数部分占 n 位
%.nf：只控制小数位数为 n

示例：

c 复制代码

float f = 3.1415926;
printf("%.2f\n", f);   // 输出：3.14
printf("%8.3f\n", f);  // 输出：   3.142

浮点精度问题

浮点数的表示范围远大于同字节整数，但其精度是有限的：

float 最大正数约为 3.4×10383.4×10^{38}3.4×1038，但有效数字只有约6~7位十进制
double 最大正数约为 1.8×103081.8×10^{308}1.8×10308，有效数字约15~16位

精度丢失现象：

由于二进制无法精确表示某些十进制小数（如 0.1），在累加或计算中可能出现误差。

示例：

c 复制代码

float f = 0.1 + 0.2;
printf("%.20f\n", f);  // 可能输出：0.30000001192092895508

浮点与`"=="`

由于浮点数是近似存储，直接使用 == 判断相等往往不可靠。

推荐做法：

定义一个小量（epsilon）进行近似判断：

c 复制代码

#include <math.h>
#define EPS 1e-6

if (fabs(a - b) < EPS) {
    printf("a 与 b 近似相等\n");
}

注意：epsilon 的值应根据实际精度需求调整。

浮点数据的组拼

在通信或数据解析中，常需要将字节流转换为浮点数。直接强制类型转换通常无效，因为整数和浮点数的内存表示完全不同。

正确方法：

方法一：使用指针类型转换

c 复制代码

int iVal = 0x40880000;  // 对应 float 4.25
float* pfVal = (float*)&iVal;
printf("%f\n", *pfVal);  // 输出：4.250000

方法二：使用联合体（union）

c 复制代码

typedef union {
    float fVal;
    unsigned char bytes[4];
    int iVal;
} FloatConvert;

FloatConvert fc;
fc.bytes[0] = 0x00;
fc.bytes[1] = 0x00;
fc.bytes[2] = 0x88;
fc.bytes[3] = 0x40;  // 小端序存储
printf("%f\n", fc.fVal);  // 输出：4.250000

注意：需考虑系统的大小端（Endian）问题，否则字节顺序可能出错。

实际编程建议

在需要高精度计算时（如金融、科学计算），优先使用 double。
避免对浮点数进行频繁的相等性判断，应使用范围判断。
在循环累加浮点数时，注意误差累积问题。
进行跨平台数据传输时，注意浮点数的字节序和格式一致性。
可使用 isnan()、isinf() 等函数检测非数值或无穷大情况。

【C语言】 浮点型（实型）变量

介绍

浮点型关键字

浮点型在内存中的存储原理

输入输出与格式控制符

浮点精度问题

浮点与"=="

浮点数据的组拼

实际编程建议

【C语言】浮点型（实型）变量

浮点与`"=="`