文章目录
-
- [1. 前缀和](#1. 前缀和)
- [2. 二维前缀和](#2. 二维前缀和)
- [3. 寻找数组的中心下标](#3. 寻找数组的中心下标)
- [4. 除自身以外数组的乘积](#4. 除自身以外数组的乘积)

1. 前缀和
题目链接:DP 34 前缀和
题目:

前缀和解决问题:快速求出数组中某一个连续区间的和。
算法思路:
- 第一步:预处理出来一个前缀和数组 dp[ i ],表示从 下标 1 到 下标 i(也就是[ 1 , i ] 区间内的和)。那么也就可以得出递推公式:dp[ i ] = dp[ i - 1 ] + arr[ i ]。
- 第二步:使用前缀和数组,快速求出某一段连续区间内的和。当题中求的是[ l , r ] 区间内的和,可以得出该区间内的和为:dp[ r ] - dp[ l - 1 ]。时间复杂度为O(q) + O(n)。
细节:该题中数组下标是从 1 开始的。因为当数组从 0 开始时,如果区间为[ 0 , i ],那么前缀和数组就会出现dp[ -1 ],此时需要进行边界条件判断,而下标从 1 开始,添加一个虚拟节点就可以直接处理边界情况。
算法代码:
java
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//1. 读入数据
int n = in.nextInt(), m = in.nextInt();
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++) arr[i] = in.nextInt();
//2. 预处理前缀和数组
long[] dp = new long[n + 1];
for (int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];
//3. 计算
while (m > 0) {
int l = in.nextInt(), r = in.nextInt();
System.out.println(dp[r] - dp[l - 1]);
m--;
}
}2. 二维前缀和
题目链接:DP 35 二维前缀和
题目:

算法思路:
-
第一步:预处理出来一个前缀和矩阵数组dp[ i ][ j ],表示从[ 1 , 1 ]位置到[ i , j ]位置这段区间里面所有元素的和。而计算dp[ i , j ]的值需要将区间进行分割计算。
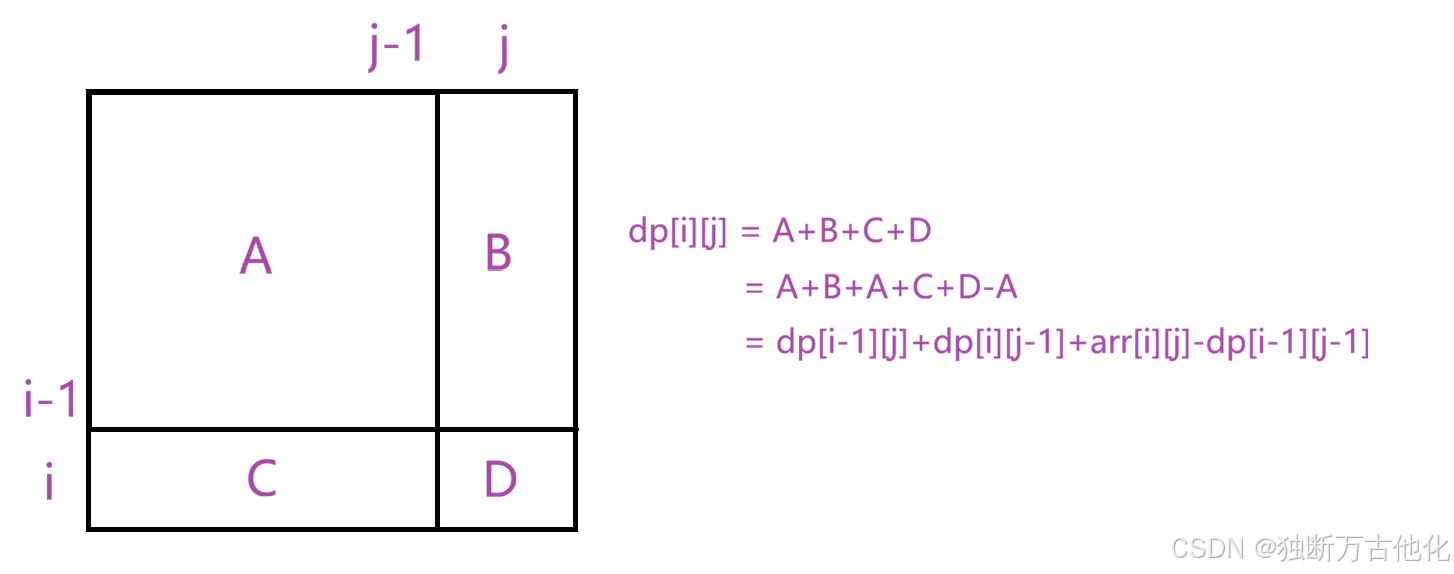
dp[ i ][ j ]的值为ABCD四块区域的和,单独的B和C不好求,但是如果将A和B,A和C放在一起求,正好就是前缀和数组中的值,此时会多求一块A区域的值,因此再单独减去即可。
所以前缀和的递推公式为:dp[ i ][ j ] = dp[ i-1 ][ j ] + dp[ i ][ j-1 ] + arr[i][j] - dp[ i-1 ][ j-1 ]。
-
第二步:使用前缀和矩阵。
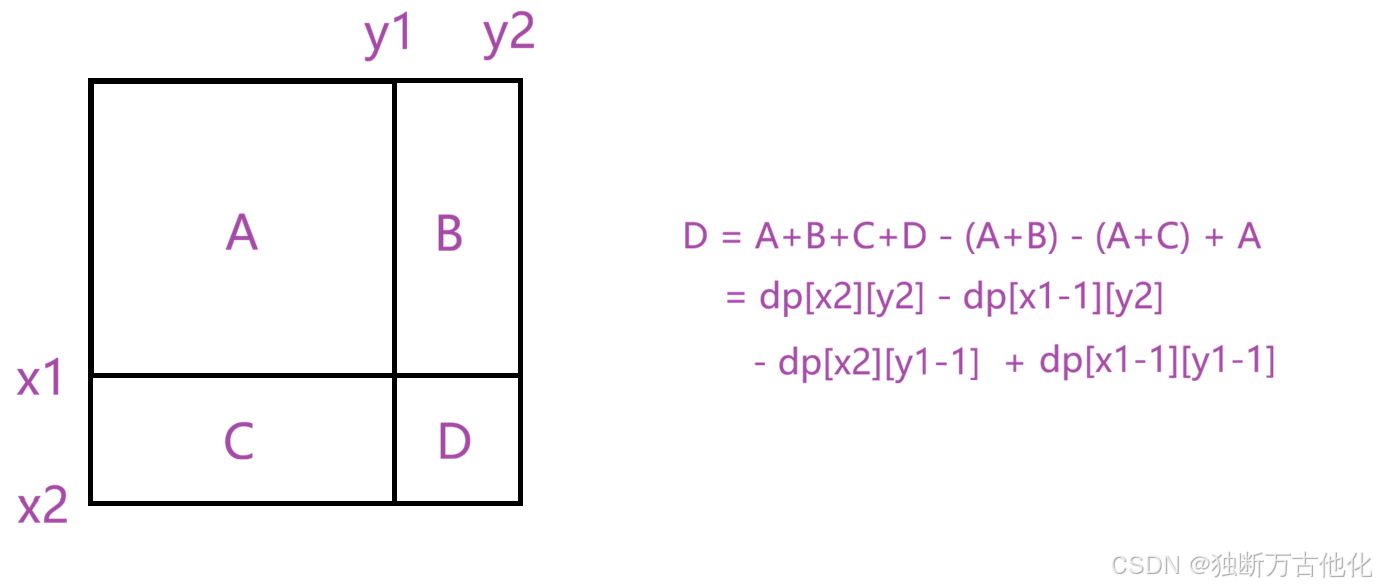
当要求的范围是( x1 , y1 ) 和 ( x2 , y2 )围成的区域,正好是D部分,而A和B,A和C 刚好是前缀和数组中的数据,因此减去这两个部分并再单独加上多减去的A部分即可。
所以得出的公式为:sum = dp[x2][y2] - dp[x1-1][y1] - dp[x2][y1-1] + dp[x1-1][y1-1]。
细节:该题中数组下标仍然是从1开始,目的和题1一样,为了减少边界情况处理。
算法代码:
java
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//1. 读入数据
int n = in.nextInt(), m = in.nextInt(), q = in.nextInt();
int[][] arr = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
arr[i][j] = in.nextInt();
//2. 预处理一个前缀和数组
long[][] dp = new long[n + 1][m + 1];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
//3. 使用前缀和数组
while (q > 0) {
int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 = in.nextInt();
System.out.println(dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1
- 1]);
q--;
}
}3. 寻找数组的中心下标
题目链接:724. 寻找数组的中心下标
题目描述:

算法思路:
- 从题中数组的中心下标定义可知,中心下标左侧的和等于中心下标右侧的和,也就是区间[ 0 , i-1 ]的和等于[ i+1 , n-1 ]。
因此可以处理出来一个前缀和数组,一个后缀和数组,然后遍历可能的中心下标,判断该处的前后缀数组的值是否相等。 - 该题的前缀和数组dp[ i ]表示的是[ 0 , i-1 ]区间所有元素的和,后缀和数组dp[ i ]表示的是[ i+1 , n-1 ]区间所有元素的和。
因此可得出递推公式,前缀和:f[ i ] = f[ i-1 ] + arr[ i-1 ];后缀和:g[ i ] = g[ i+1 ] + arr[ i+1 ]。
细节:当i 为 0 时,会发生越界访问情况,此时f[ i-1 ]会越界,同理,g[ i+1 ]也会发生越界情况。因此需要提前处理边界情况,使f[ 0 ] = g[ n-1 ] = 0,并且下标分别从 1 和 n-2 开始。
算法代码:
java
public int pivotIndex(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
for (int i = 1; i < n; i++) {
f[i] = f[i-1] + nums[i-1];
}
for (int i = n-2; i >= 0; i--) {
g[i] = g[i+1] + nums[i+1];
}
for (int i = 0; i < n; i++) {
if(f[i] == g[i]) return i;
}
return -1;
}4. 除自身以外数组的乘积
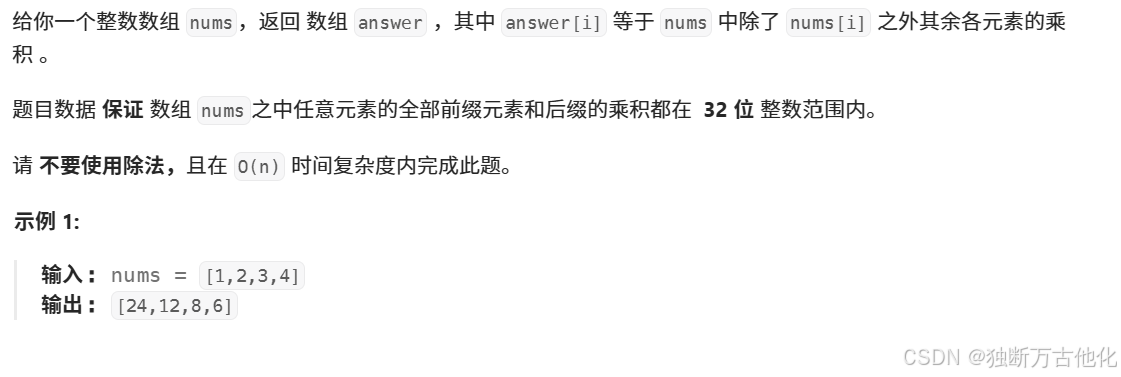
题目链接:238. 除自身以外数组的乘积
题目描述:
算法思路:
- 根据题意,每一个位置的结果都是由该元素左侧的乘积和右侧的乘积相乘得到,因此也可以预处理出来两个数组。思路解法和上题几乎一样。
- 分别为前缀积和后缀积数组。而前缀积f[ i ]表示的为[ 0 , i-1 ]区间内所有元素的乘积,后缀积g[ i ]表示[ i+1 , n-1 ]区间内所有元素的乘积。
- 因此得到递推公式前缀积:f[ i ] = f[ i-1 ]×nums[ i-1 ];后缀积:g[ i ] = g[ i+1 ]×nums[ i+1 ]。
细节:该题不一样的点在于边界情况时,因为边界元素值为0,当计算时所有的结果都为0,因此需要提前处理边界的值为1。
算法代码:
java
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
//前缀和
int[] f = new int[n];
//后缀和
int[] g = new int[n];
f[0] = g[n-1] = 1;
int[] ret = new int[n];
for (int i = 1; i < n; i++) {
f[i] = f[i-1]*nums[i-1];
}
for (int i = n-2; i >= 0; i--) {
g[i] = g[i+1]*nums[i+1];
}
for (int i = 0; i < n; i++) {
ret[i] = f[i]*g[i];
}
return ret;
}