二叉树链式结构的实现1

前言
嗨,我是firdawn,本章将简单介绍,二叉树的遍历方式,以及如何判断二叉树的节点个数,叶子个数,高度,在本章的末尾,我将给出一些二叉树基础练习题,供大家练习巩固知识点。我们学习二叉树,其实本身并没有太多意义,不过我们后面学的搜索二叉树会用到二叉树,所以我们先学习二叉树的一些基础知识以及使用,为后面的学习打一下基础。下面的图是本章的思维导图,那么,让我们开始吧!
一,粗糙创建二叉树
在学习对二叉树的遍历前,我们需要创建一颗二叉树。不过呢,由于我们目前对二叉树的掌握不够深入,所以我们先暴力手搓一个二叉树,等我们对二叉树了解得差不多了,我们再来研究二叉树的真正创建方式。
c
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->_left = node2;
node1->_right = node4;
node2->_left = node3;
node4->_left = node5;
node4->_right = node6;我们创建的二叉树的结构图如下图1.1-1:
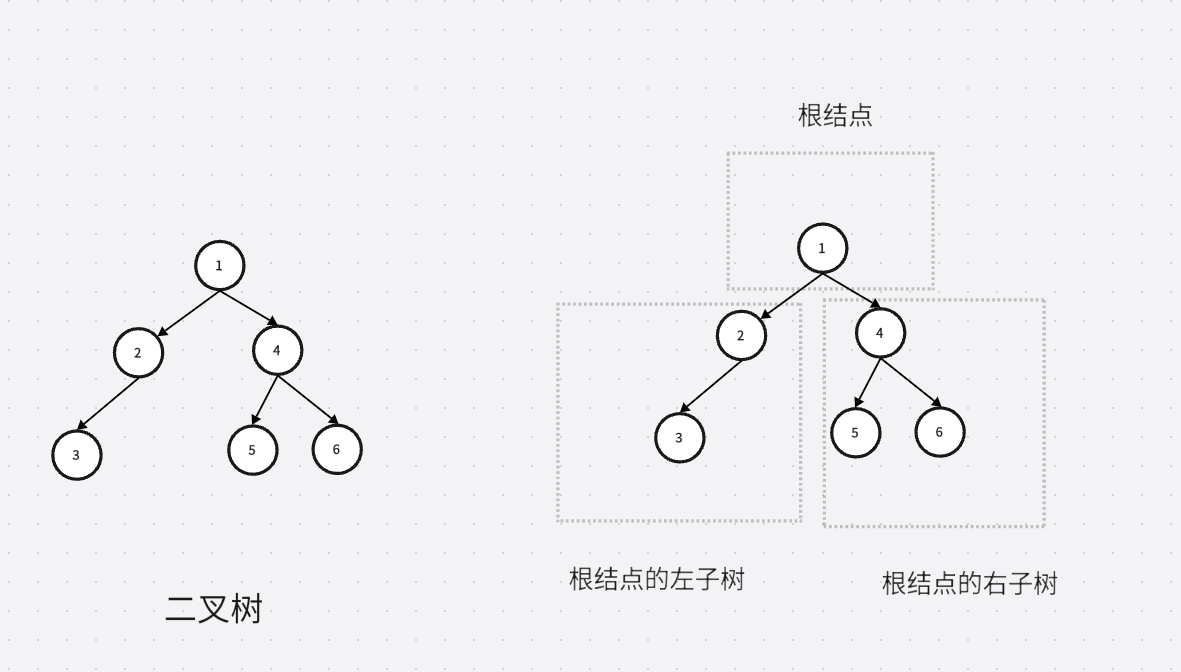
二,二叉树的遍历
在学习二叉树的遍历前,我们先来简单回顾一下二叉树的概念,二叉树是:
1.空树
2.非空:根结点,左子树,右子树构成
在看到任何一个二叉树时,我们都要有这个意识,我们要把看到的二叉树分为根,左子树和右子树。而左子树又分为根,左子树和右子树,右子树也一样。
2.1前序、中序以及后序遍历
二叉树的遍历是二叉树上最重要的运算之一,也是二叉树进行其他运算的基础。
二叉树的遍历分为:前序遍历,中序遍历,后序遍历
- 前序遍历(Preorder Traversal):前序遍历也被称为前根遍历,前序遍历每次访问都分为根,左子树,右子树。
- 中序遍历(Inorder Traversal):中序遍历也被称为前根遍历,中序遍历每次访问都分为左子树,根,右子树。q
- 后序遍历(Postorder Traversal):后序遍历也被称为前根遍历,后序遍历每次访问都分为左子树,右子树,根。
我们先使用图1.1-1的二叉树来练习一下二叉树的三种遍历方式。
1.前序遍历:从 1 这颗树开始,遍历顺序分为根,左子树,右子树,先访问1,再访问 1 这个结点的左子树,右子树。访问完结点1之后,我们先来访问1的左子树 2 ,访问 2 这颗树也分为根,左子树,右子树。访问完 2 之后,再访问 2 的左子树,右子树。我们先访问 2 的左子树 3 ,先访问 3 ,再访问 3 的左子树,右子树。 3 的左子树为空,空结点为最小的子树,由于空返回到 3 ,再访问 3 的右子树,3 的右子树为空,再访问 2 的右边, 2 的右边为空,再访问1的右边,先访问 4 ,再访问4的左边,先访问5,再访问5的左边,5的左边为空,再访问5的右边,5 的右边为空,再访问 6 ,访问完 6 ,再访问 6 的左边,6 的左边为空,再访问 6 的右边。访问到空节点就打印"N",访问到不为空的结点就打印该结点的值。结果如下图2.1-1:
2.中序遍历:中序遍历的顺序遵循:左子树,根,右子树的访问顺序。先访问1的左子树,1的左子树是2,再访问2的左子树,2的左子树为3,再访问3的左子树,3的左子树为空,再访问3,再访问3的右子树,3的右子树为空,再访问2,再访问2的右子树,再访问1,再访问1的右子树,1的右子树为4,再访问4的左子树,4的左子树为5,再访问5的左子树,5的左子树为空,访问到空结点就返回,再访问5,再访问5的右子树,再访问4,再访问4的右子树,4的右子树为6,在访问6的左子树,6的左子树为空,遇到空就返回,再访问6,再访问6的右子树,6的右子树为空,遇到空就返回。
3.后序遍历:后序便利就先不列举了,执行逻辑和前面类似。
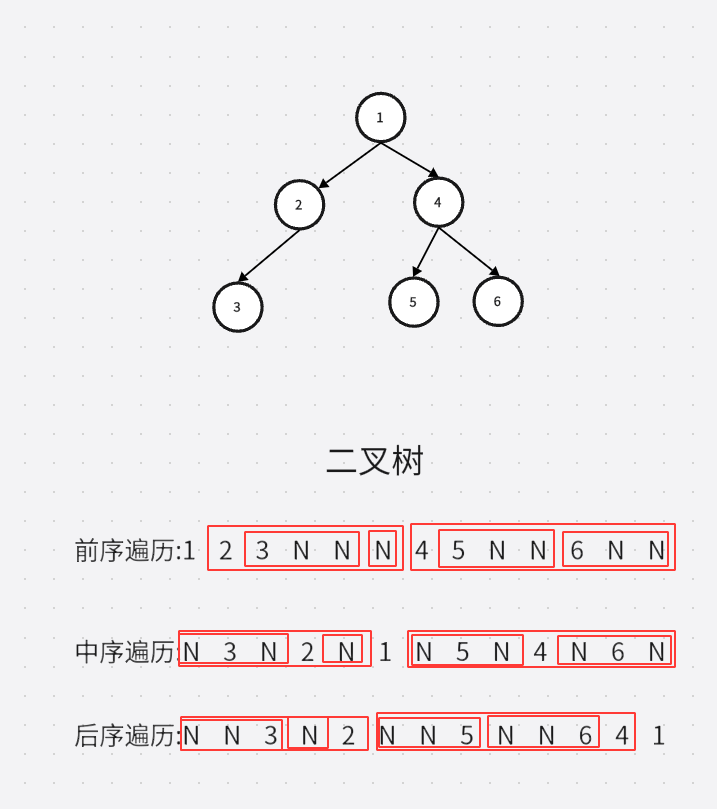
我们讲完三种遍历方式的逻辑运行过程,那么它们的代码怎么写呢?以下是实现这三种遍历方式的代码.
前序遍历的代码实现:
c
//前序遍历
void FrontOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->val);
FrontOrder(root->left);
FrontOrder(root->right);
}中序遍历的代码实现:
c
/中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}后序遍历的代码实现:
c
//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}以前序遍历为例,怎么理解这块代码,为什么这样写就能实现前序遍历呢?以下是前序遍历程序执行过程的逻辑过程,我们用递归展开图来理解代码的运行。
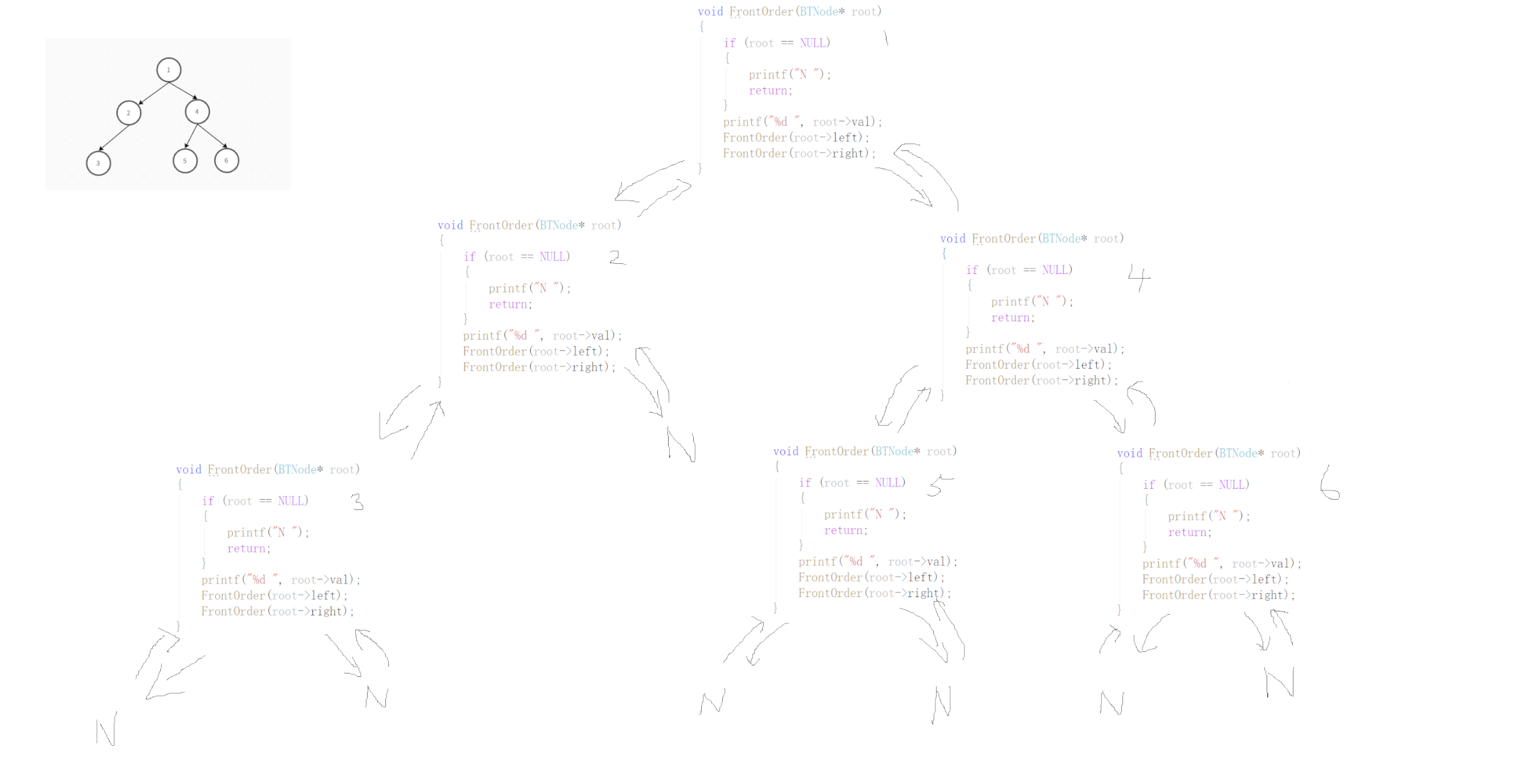
前序遍历的物理过程就是在内存中建立栈帧,以下为前序遍历的物理执行过程:
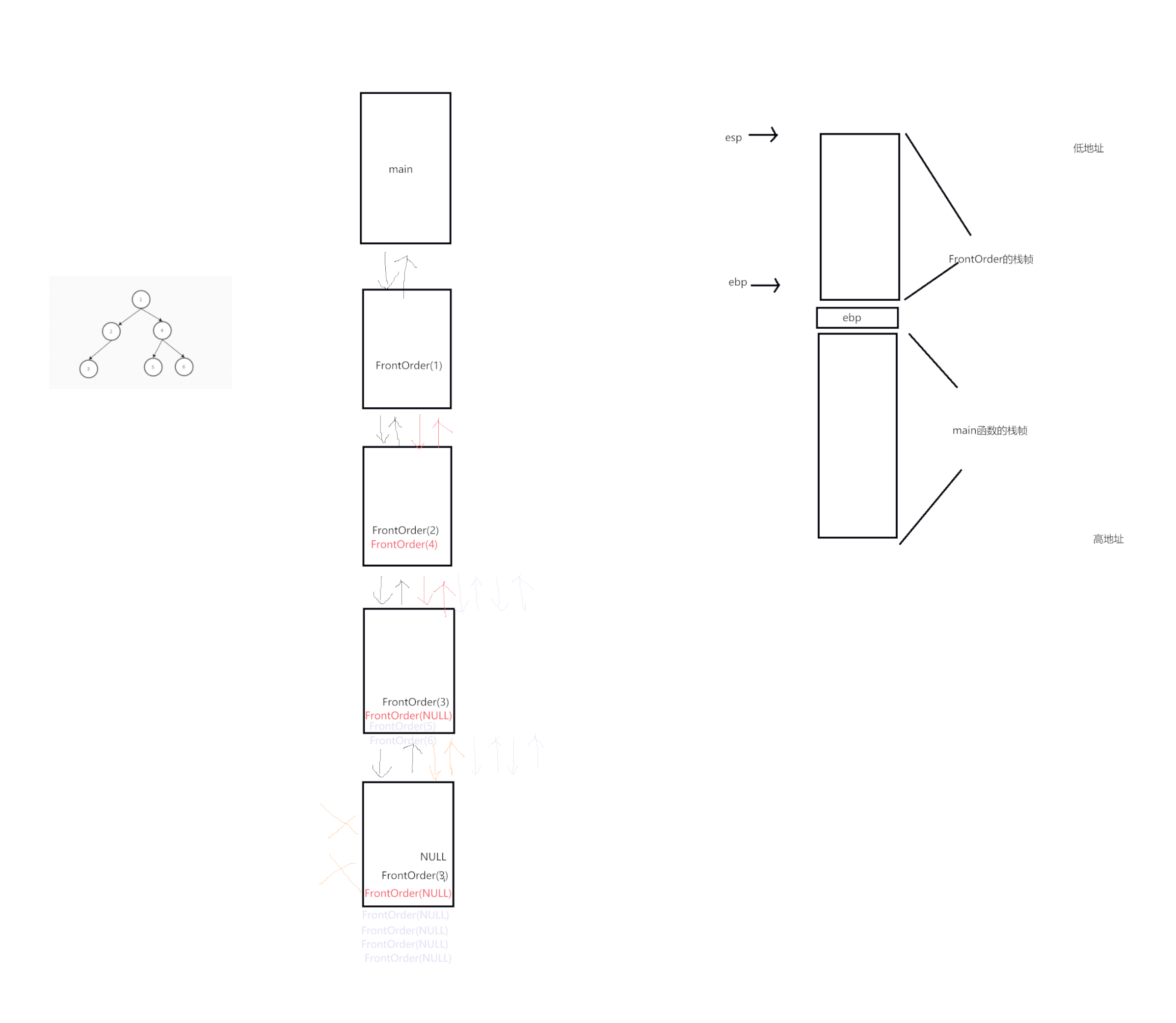
2.2层序遍历
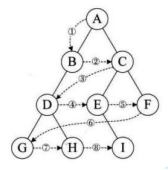
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
三,结点个数以及高度等
二叉树结点个数:
c
//二叉树结点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}二叉树叶子结点个数:
c
//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}二叉树高度:
c
//二叉树高度
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int left = BinaryTreeHeight(root->left);
int right = BinaryTreeHeight(root->right);
return left > right ? left + 1 : right + 1;
}四,二叉树基础OJ练习
答案:
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool _isUnivalTree(struct TreeNode* root,int val)
{
if(root==NULL)
{
return true;
}
if(root->val!=val)
{
return false;
}
return _isUnivalTree(root->left,val) && _isUnivalTree(root->right,val);
}
bool isUnivalTree(struct TreeNode* root) {
//遍历判断
//return _isUnivalTree(root,root->val);
//用分治思想解决
//为空 返回ture
//不为空 根和左子树相等,根和右子树相等并且左右子树都为单值二叉树时,该树为单值二叉树
//
if(root==NULL)
{
return true;
}
if(root->left && root->left->val!=root->val)
{
return false;
}
if(root->right && root->right->val!=root->val)
{
return false;
}
return isUnivalTree(root->left) && isUnivalTree(root->right);
}答案:
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root) {
//使用分治思想实现
//为空 返回0
//不为空 返回左子树的高度 右子树的高度更大的那个+1
if(root==NULL)
{
return 0;
}
int left=maxDepth(root->left);
int right=maxDepth(root->right);
return left>right?left+1:right+1;
}