摘要
本周继续学习了强化学习的相关知识,了解和强化学习的核心思想蒙特卡洛方法与策略梯度算法的原理
abstract
This week, I continued studying reinforcement learning, gaining an understanding of its core concepts, including the principles of the Monte Carlo method and the policy gradient algorithm.
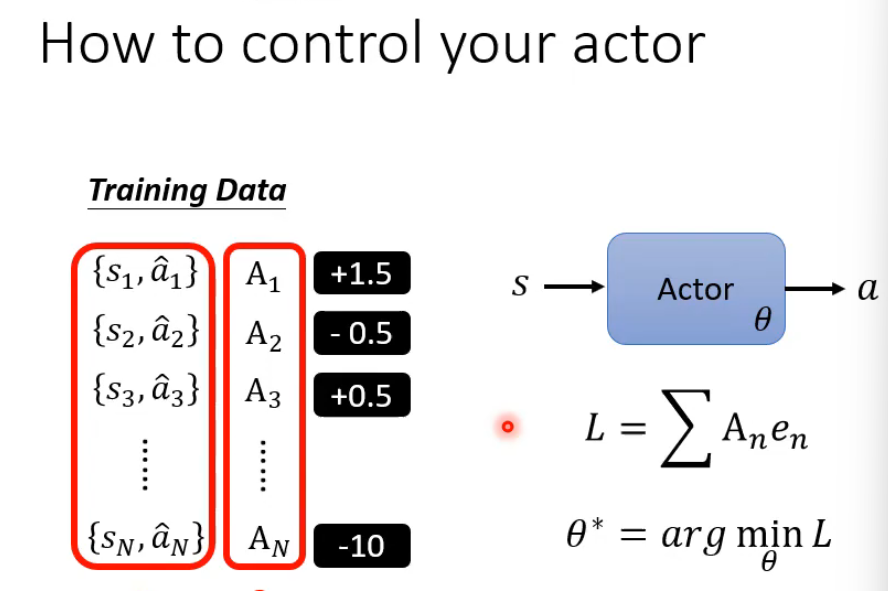
基于优势函数的策略梯度方法用于训练智能体的策略网络
其核心思想是利用一系列状态-动作对 {st,at}{st,a^} 及其对应的优势值 AtAt(正数表示动作优于平均水平,负数则相反)来引导策略更新。通过构建损失函数 L,其中 en 通常为动作的负对数概率,将优势值作为权重,使得智能体在优化参数 θ 以最小化 L 的过程中,更多地学习优势高的动作,抑制优势低的动作。最终,训练好的策略网络能够根据输入状态 s输出更优的动作 a,从而提高累积奖励。这种方法结合了监督学习(给定目标动作)和强化学习(优势加权)的特点,以实现更稳定高效的学习。
蒙特卡洛方法
蒙特卡洛方法是一种基于完整回合经验评估动作价值的直观方法。它的核心思想是通过实际游戏结果来衡量动作的优劣,而不是依赖预测或估计。具体来说,当智能体在某个状态执行某个动作后,我们会等待整个游戏或任务回合结束,记录从该时刻起获得的所有奖励总和(称为回报),然后将这个实际回报与当前状态下预期的平均回报进行比较,其差值即为优势值。

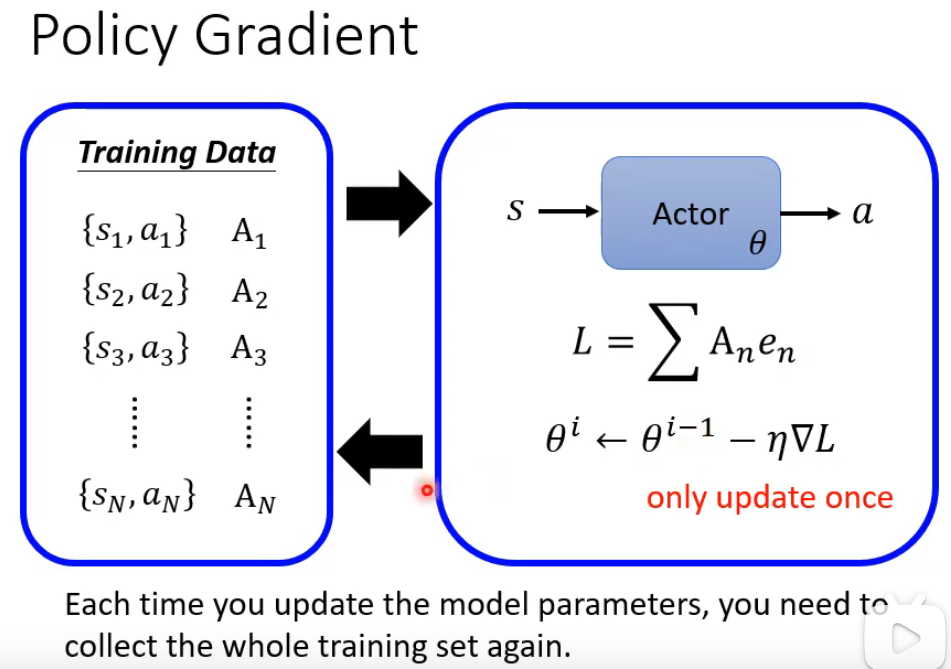
Policy Gradient
策略梯度(Policy Gradient)算法的核心训练流程及其关键限制。它首先通过当前策略网络(Actor)与环境交互收集一批状态-动作对数据,并为每个动作计算优势值 AnAn 以衡量其相对优劣。随后使用这些数据构建损失函数 L,并通过梯度下降对策略参数 θθ进行一次更新,每次参数更新后,必须丢弃当前数据并重新收集完整的训练集