彻底掌握 RNN（实战）：PyTorch API 详解、多层RNN、参数解析与输入机制

All The Way North-2026-02-02 19:42

文章目录

  • [24、RNN - API 基本使用](#24、RNN - API 基本使用)
  • [25、RNN 如何预测](#25、RNN 如何预测)
  • [26、多层RNN（`num_layers > 1`）](#26、多层RNN（num_layers > 1）)
  • [27、RNN - API 进阶使用](#27、RNN - API 进阶使用)
  • [28、PyTorch里输入到底有几个------1个 or 2个](#28、PyTorch里输入到底有几个——1个 or 2个)
  • 29、代码：

本篇文章紧接着上一篇RNN理论篇：万字长文 · 彻底掌握RNN：原理、隐藏状态、矩阵变换、底层公式、单/Batch 样本处理、计算示例等深度解析

24、RNN - API 基本使用

🌟 场景设定：我们要处理两句话

假设我们有以下两句话（每句 3 个词）：

  • 句子 A ：["猫", "追", "狗"]
  • 句子 B ：["我", "爱", "猫"]

我们有一个小词表（共 4 个词）：

text 复制代码 
词表 = ["猫", "追", "狗", "我", "爱"] → 共 5 个词
索引：   0     1     2     3     4

第一步：把词变成向量（one-hot 编码）

每个词用一个 5 维 one-hot 向量 表示（因为词表大小 = 5）：

  • "猫" → [1, 0, 0, 0, 0]
  • "追" → [0, 1, 0, 0, 0]
  • "狗" → [0, 0, 1, 0, 0]
  • "我" → [0, 0, 0, 1, 0]
  • "爱" → [0, 0, 0, 0, 1]

所以：

  • 句子 A →

    python 复制代码 
    [
  [1, 0, 0, 0, 0],  # "猫"
  [0, 1, 0, 0, 0],  # "追"
  [0, 0, 1, 0, 0]   # "狗"
]

  • 句子 B →

    python 复制代码 
    [
  [0, 0, 0, 1, 0],  # "我"
  [0, 0, 0, 0, 1],  # "爱"
  [1, 0, 0, 0, 0]   # "猫"
]

第二步：把两个句子叠成一个三维张量（这就是 RNN 的输入！）

python 复制代码 
import torch

x = torch.tensor([
  [                     # ← 句子 A
    [1., 0., 0., 0., 0.],  # 第1个词："猫"
    [0., 1., 0., 0., 0.],  # 第2个词："追"
    [0., 0., 1., 0., 0.]   # 第3个词："狗"
  ],
  [                     # ← 句子 B
    [0., 0., 0., 1., 0.],  # 第1个词："我"
    [0., 0., 0., 0., 1.],  # 第2个词："爱"
    [1., 0., 0., 0., 0.]   # 第3个词："猫"
  ]
])

✅ 这个 x 的形状是 (2, 3, 5)，含义：

  • 2：2 个句子（batch size = 2）
  • 3：每句 3 个词（sequence length = 3）
  • 5：每个词是 5 维向量（input_size = 5）

🔔 这就是 RNN 的标准输入格式（当 batch_first=True 时）

⚙️ 第三步：创建 RNN 层（解释每个参数）

python 复制代码 
import torch.nn as nn

rnn = nn.RNN(
    input_size=5,      		# ✅ 必须等于 x 的最后一维（5）  （注意：只针对第0层RNN，后面有详情）
    hidden_size=2,     		# ✅ 我们希望"记忆"是 2 维的（比如 [开心程度, 动作强度]）。
    num_layers=1,      		# 先用 1 层（简单）
    batch_first=True,  		# ✅ 关键！让输入是 (句子数, 词数, 词维)
    bias=True,         		# 加偏置（默认 True，先不管）
    nonlinearity='tanh' 	# 激活函数（默认 tanh）
)

💡 hidden_size=2 是什么意思？

就是说，机器人每读一个词，会更新一个 2 维的记忆向量 ，比如 [0.3, -0.7]。

这个向量会传给下一个词。

注意：input_size=5 只是针对第0层RNN，如果 num_layers 大于 1，之后的RNN层的 input_size 就不是5了，后面有详情

🔄 第四步：运行 RNN，看它返回什么

python 复制代码 
# 前向传播
output, hidden = rnn(x)

RNN 会返回 两个东西：

🔹 返回值 1：output ------ 所有时刻的记忆

  • 含义 ：对每个句子，记录它在每个词之后的记忆。
  • 形状 ：(batch_size, seq_len, hidden_size) = (2, 3, 2)
python 复制代码 
print("output.shape =", output.shape)  # (2, 3, 2)
  • output[0] → 句子 A 的 3 个记忆（读完第1、2、3个词后）
  • output[1] → 句子 B 的 3 个记忆

具体来说：

  • output[0, 0, :] = 句子 A 读完"猫"后的记忆（2 维）
  • output[0, 1, :] = 句子 A 读完"追"后的记忆
  • output[0, 2, :] = 句子 A 读完"狗"后的记忆（最终记忆）

同理：

  • output[1, 2, :] = 句子 B 读完"猫"后的最终记忆

🔹 返回值 2：hidden ------ 最后一刻的记忆

  • 含义 ：只取最后一个词之后的记忆（常用于分类任务）
  • 形状 ：(num_layers, batch_size, hidden_size) = (1, 2, 2)
python 复制代码 
print("hidden.shape =", hidden.shape)  # (1, 2, 2)
  • hidden[0, 0, :] = 句子 A 的最终记忆
  • hidden[0, 1, :] = 句子 B 的最终记忆

✅ 并且：
hidden[0, 0, :] == output[0, -1, :]
hidden[0, 1, :] == output[1, -1, :]

🧪 第五步：完整代码 + 打印结果

python 复制代码 
import torch
import torch.nn as nn

torch.manual_seed(66)

# 输入：2 个句子，每句 3 个词，每个词 5 维
x = torch.tensor([
  [[1., 0., 0., 0., 0.], [0., 1., 0., 0., 0.], [0., 0., 1., 0., 0.]],  # 句子 A
  [[0., 0., 0., 1., 0.], [0., 0., 0., 0., 1.], [1., 0., 0., 0., 0.]]   # 句子 B
])

# 创建 RNN
rnn = nn.RNN(input_size=5, hidden_size=2, batch_first=True)

# 前向计算
output, hidden = rnn(x)

# 打印形状
print("输入 x 形状:", x.shape)        # (2, 3, 5)
print("output 形状:", output.shape)   # (2, 3, 2)
print("hidden 形状:", hidden.shape)   # (1, 2, 2)

# 打印具体内容（数值每次运行可能不同，因为权重随机初始化）
print("\n句子 A 的记忆序列（output[0]）:")
print(output[0])
# tensor([[0.6412, 0.7201],
#         [0.3475, 0.4216],
#         [0.4970, 0.4756]], grad_fn=<SelectBackward0>)

print("\n句子 B 的记忆序列（output[1]）:")
print(output[1])
# tensor([[0.6981, 0.7617],
#         [0.9120, 0.0942],
#         [0.5178, 0.3952]], grad_fn=<SelectBackward0>)

print("\n句子 A 的最终记忆（hidden[0, 0]）:")
print(hidden[0, 0])
# tensor([0.4970, 0.4756], grad_fn=<SelectBackward0>)

print("\n验证：hidden[0,0] 是否等于 output[0, -1]?")
print(torch.allclose(hidden[0, 0], output[0, -1]))    #  True

📌 第六步：关键总结（用两个句子举例）

问题 答案
RNN 输入是什么？ 一批句子，每个词是向量 → 形状 (2, 3, 5)
input_size=5 为什么？ 因为每个词是 5 维（词表大小=5）
hidden_size=2 代表什么？ 每个句子在每个时刻都有一个 2 维"记忆"
output 是什么？ 所有时刻的记忆 → (2, 3, 2) • 第0行：句子A的3个记忆 • 第1行：句子B的3个记忆
hidden 是什么？ 最后时刻的记忆 → (1, 2, 2) • hidden[0,0] = 句子A最终记忆 • hidden[0,1] = 句子B最终记忆
output 和 hidden 有什么关系？ hidden[0, i] == output[i, -1]（对每个句子 i 都成立）

❓ 常见疑问解答

Q：为什么 hidden 的第一维是 1？

因为 num_layers=1。如果你堆了 2 层 RNN，那就有 2 个最终记忆（每层一个），hidden 就会是 (2, 2, 2)。

Q：我可以只用 hidden 吗？

✅ 可以！比如做情感分析：

  • 用 hidden[0, 0] 判断句子 A 是正面还是负面
  • 用 hidden[0, 1] 判断句子 B

Q：如果我想用每个词的记忆（比如做词性标注）？

✅ 用 output！

  • output[0, 0] → 给"猫"打标签
  • output[0, 1] → 给"追"打标签
  • ...

❤️ 最后提醒

  • 始终设置 batch_first=True ，否则输入要写成 (3, 2, 5)，非常反直觉。
  • input_size 必须匹配你词向量的维度。
  • output 包含全过程，hidden 只包含最后一步。
  • 两个句子的计算是完全独立的！RNN 不会把句子 A 的记忆混到句子 B 里。

25、RNN 如何预测

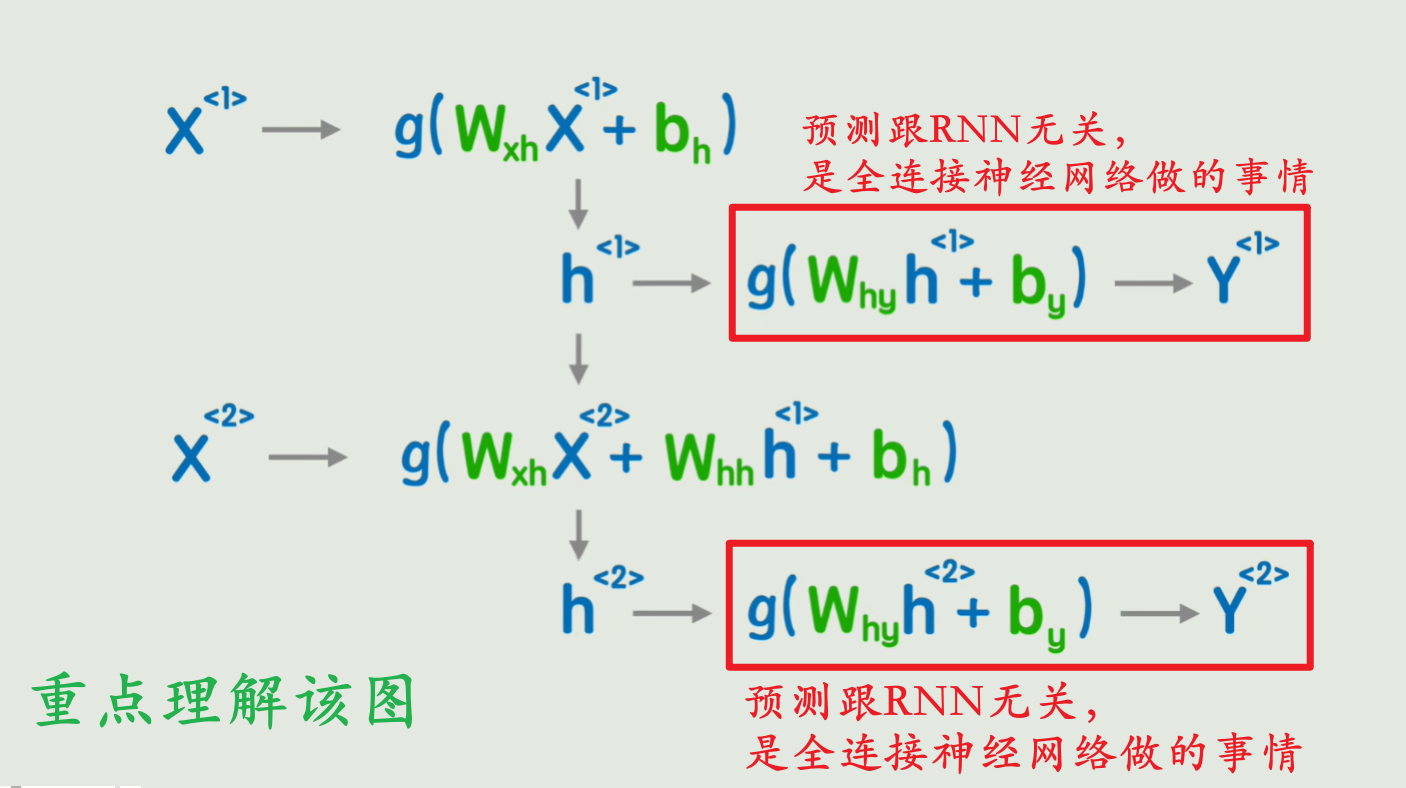
不涉及复杂公式，不用先验知识，只用你熟悉的两个句子 + 一个目标：让 RNN 学会"猜下一个词"。

🎯 一、RNN 预测的核心思想（一句话）

RNN 通过"记住前面说了什么"，来预测"接下来最可能说什么"。

就像你读到 "我 爱 ___"，大脑会自动想到 "猫"、"你"、"巧克力"......

RNN 做的，就是这件事------只不过它用的是数学和向量。

🧩 二、举个具体例子

假设我们有大量类似这样的句子：

  • "猫 追 狗"
  • "狗 追 猫"
  • "我 爱 猫"
  • "我 爱 你"

我们的目标是：

👉 给定前两个词，让 RNN 预测第三个词。

比如：

  • 输入："我 爱" → 预测："猫" 或 "你"
  • 输入："猫 追" → 预测："狗"

这就是语言建模（Language Modeling），也是 RNN 最经典的预测任务。

🔧 三、RNN 预测需要哪些组件？

要完成预测，RNN 模型其实包含 两个部分：

组件 作用 PyTorch 对应
1. RNN 层 读入词序列，生成"记忆"（隐藏状态 h） nn.RNN(...)
2. 输出层 把"记忆"转换成"对每个词的打分" nn.Linear(hidden_size, vocab_size)

✅ 注意：nn.RNN 本身不直接输出预测结果 ！

它只负责生成 h。真正的预测靠后面的线性层。

🔄 四、预测的完整流程（一步一步）

我们以输入 "我 爱" 为例，看看 RNN 怎么一步步预测下一个词。

步骤 1️⃣：把词变成向量

词表 = ["猫", "追", "狗", "我", "爱"] → 共 5 个词

  • "我" → [0, 0, 0, 1, 0]
  • "爱" → [0, 0, 0, 0, 1]

输入张量：

python 复制代码 
x = [
  [0, 0, 0, 1, 0],   # "我"
  [0, 0, 0, 0, 1]    # "爱"
]  # 形状 (2, 5)

（实际代码中会加 batch 维度 → (1, 2, 5)）

步骤 2️⃣：RNN 读入这两个词，生成"最终记忆"

python 复制代码 
rnn = nn.RNN(input_size=5, hidden_size=4, batch_first=True)
output, hidden = rnn(x.unsqueeze(0))  # x 变成 (1, 2, 5)
  • hidden 的形状是 (1, 1, 4)
  • hidden[0, 0, :] 就是 RNN 读完 "我 爱" 后的内部记忆（一个 4 维向量）

💡 这个向量编码了："前面说了'我 爱'，现在情绪是温暖的，大概率接一个名词或人称"

步骤 3️⃣：用这个"记忆"去预测下一个词

我们加一个输出层（全连接层）：

python 复制代码 
linear = nn.Linear(in_features=4, out_features=5)  # 5 = 词表大小
logits = linear(hidden[0, 0, :])  # 得到一个 5 维向量
  • logits = [2.1, -0.5, 1.8, -1.0, 0.3]
  • 每个数字对应一个词的"得分"：
    • 索引 0（"猫"）: 2.1 ← 最高！
    • 索引 1（"追"）: -0.5
    • 索引 2（"狗"）: 1.8
    • 索引 3（"我"）: -1.0
    • 索引 4（"爱"）: 0.3

步骤 4️⃣：把得分转成"概率"

用 softmax 把得分变成概率：

python 复制代码 
probs = torch.softmax(logits, dim=0)
# probs ≈ [0.60, 0.05, 0.30, 0.01, 0.04]

✅ 解读：

  • 下一个词是 "猫" 的概率 ≈ 60%
  • 是 "狗" 的概率 ≈ 30%
  • 其他词概率很低

步骤 5️⃣：做出预测

  • 取最大概率 ：predicted_index = probs.argmax() → 0
  • 查词表 ：word = vocab[0] → "猫"

🎉 预测结果："我 爱 猫"

🟩 🔒 重要限制：模型只能预测词库中的词！

RNN 的预测结果永远只能是训练时构建的词表（vocabulary）里的词。

为什么？因为输出层的大小是 vocab_size，每个位置对应词表中的一个词。

模型根本不知道词表之外的词长什么样------它连这些词的 ID 都没有！

例如，如果你的词表是 ["猫", "追", "狗", "我", "爱"]，那么模型永远不可能输出：

  • "月亮"
  • "悲伤"
  • "周杰伦"

即使这些词在语义上很合理，只要它们没出现在训练词表里，模型就无法生成。

💡 这不是缺陷，而是这类模型的基本设计：它通过组合已知词来创造新句子，而不是发明新词 。

在歌词生成任务中，只要词表覆盖了原歌词的大部分词汇，效果就会很好。

📊 五、训练 vs 预测的区别（关键！）

阶段 输入 目标 RNN 做什么
训练 完整句子（如 "我 爱 猫"） 让模型学会：看到 "我 爱" 就输出 "猫" 用真实标签计算损失，更新权重
预测（推理） 部分句子（如 "我 爱"） 生成最可能的下一个词 用学到的权重做前向传播，输出概率

🔔 训练时，RNN 会同时看到所有词 ；
预测时，RNN 只能看到已有的词，然后猜下一个。

🧠 六、为什么能预测？------因为"记忆"包含了上下文

RNN 的魔法在于：

  • 读第一个词 → 产生初步记忆
  • 读第二个词 → 结合新词 + 旧记忆 → 更新记忆
  • 最终记忆 = 整个上下文的压缩表示

所以：

  • "我 爱" → 记忆偏向"情感+人称"
  • "猫 追" → 记忆偏向"动作+动物"

不同的上下文 → 不同的记忆 → 不同的预测！

🛠️ 七、PyTorch 完整预测代码（极简版）

python 复制代码 
import torch
import torch.nn as nn

torch.manual_seed(66)

# 词表
vocab = ["猫", "追", "狗", "我", "爱"]
vocab_size = len(vocab)

# 模型
rnn = nn.RNN(input_size=vocab_size, hidden_size=4, batch_first=True)
linear = nn.Linear(4, vocab_size)

# 输入："我 爱"
x = torch.tensor([[[0,0,0,1,0], [0,0,0,0,1]]], dtype=torch.float32)  # (1, 2, 5)

# 前向传播
_, hidden = rnn(x)                     # hidden: (1, 1, 4)
logits = linear(hidden[0, 0])          # (5,)
probs = torch.softmax(logits, dim=0)

# 预测
pred_idx = probs.argmax().item()
print(f"预测下一个词是: {vocab[pred_idx]}")    # 爱  (注意, 这里的全连接神经网络没有经过训练，预测错非常正常)
print(f"各词概率: {dict(zip(vocab, probs.tolist()))}")
# {'猫': 0.1471, '追': 0.1489, '狗': 0.1734, '我': 0.1424, '爱': 0.3880}   # 只截取了前4位小数

✅ 八、总结：RNN 预测的 5 个关键点

  1. RNN 本身不直接预测 ，它只生成"记忆"（隐藏状态 h）。
  2. 真正的预测靠一个额外的线性层 （Linear(hidden_size, vocab_size)）。
  3. 预测是逐词进行的：给前 n 个词，猜第 n+1 个词。
  4. "记忆" h 编码了所有历史信息，是预测的核心。
  5. 训练时用完整句子监督学习，预测时用部分句子生成新内容。

你现在可以自信地说：

"我知道 RNN 是怎么预测的了！它不是魔法，而是一个'读上下文 → 生成记忆 → 打分选词'的过程。"

26、多层RNN（num_layers > 1）

下面我将为你完整、清晰、逐层、逐维度地解释多层 RNN（num_layers > 1）中数据的流动过程 ，并使用一组精心设计的、各维度互不相同的数值 ，避免像 (2,2) 这样容易混淆的情况。

我们将以 num_layers = 3 的 RNN 为例，配合详细的 NLP 场景解释和张量形状追踪，确保你彻底理解每一层的输入/输出是什么、为什么这样设计、以及 PyTorch 是如何自动处理维度匹配的。

🧩 一、设定一个"全不同"的例子（避免任何维度重复）

我们设定以下超参数（全部不同）：

参数 值 NLP 含义
batch_size 4 一批中有 4 个句子
seq_len 6 每个句子有 6 个词 （不足补 <PAD>）
input_size 10 每个词用 10 维词向量 表示（如来自 nn.Embedding）
hidden_size 8 RNN 隐藏状态维度为 8
num_layers 3 使用 3 层 RNN 堆叠

✅ 所有数字都不同：4, 6, 10, 8, 3 → 不会混淆！

我们使用 batch_first=True（推荐），所以输入形状为：

python 复制代码 
x.shape = (4, 6, 10)
# 含义：(4个句子, 每句6个词, 每个词10维向量)

🏗️ 二、构建 RNN 模型

python 复制代码 
import torch
import torch.nn as nn

rnn = nn.RNN(
    input_size=10,      # 第0层的输入维度（原始词向量）
    hidden_size=8,      # 所有层的隐藏状态维度
    num_layers=3,       # 3层堆叠
    batch_first=True    # 输入/输出格式：(batch, seq_len, *)
)

🔍 注意：虽然只写了一个 input_size=10，但 只有第 0 层用它 ，第 1、2 层的输入维度会自动设为 hidden_size=8。

🔁 三、逐层数据流动详解（核心部分）

▶ 第 0 层（底层，Layer 0）

  • 输入：原始词向量

    python 复制代码 
    x₀ = x  # shape: (4, 6, 10)
    • 4 个句子
    • 每句 6 个词
    • 每个词 10 维

  • RNN 权重：

    • weight_ih_l0: shape (8, 10) → 将 10 维输入映射到 8 维隐藏状态
    • weight_hh_l0: shape (8, 8)

  • 输出（即该层对每个词的理解）：

    python 复制代码 
    out₀ = [h₀₀, h₀₁, ..., h₀₅]  # 共6个时间步
out₀.shape = (4, 6, 8)
    • 4 个句子
    • 每句 6 个词
    • 每个词被表示为 8 维上下文向量

✅ 这一层完成了：从原始词向量 → 初级上下文表示

▶ 第 1 层（中间层，Layer 1）

  • 输入 ：第 0 层的输出 out₀

    python 复制代码 
    x₁ = out₀  # shape: (4, 6, 8)
    • 不再看原始 10 维词向量！
    • 而是看第 0 层对每个词的 8 维理解

  • RNN 权重（PyTorch 自动创建）：

    • weight_ih_l1: shape (8, 8) ← 输入维度是 8，不是 10！
    • weight_hh_l1: shape (8, 8)

  • 输出：

    python 复制代码 
    out₁ = [h₁₀, h₁₁, ..., h₁₅]
out₁.shape = (4, 6, 8)

✅ 这一层完成了：在初级理解基础上，提炼更抽象的语义特征

▶ 第 2 层（顶层，Layer 2）

  • 输入 ：第 1 层的输出 out₁

    python 复制代码 
    x₂ = out₁  # shape: (4, 6, 8)

  • RNN 权重：

    • weight_ih_l2: shape (8, 8)
    • weight_hh_l2: shape (8, 8)

  • 输出：

    python 复制代码 
    out₂ = [h₂₀, h₂₁, ..., h₂₅]
out₂.shape = (4, 6, 8)

✅ 这一层输出的是最终的、最高层次的序列表示

📤 四、最终返回值

调用 output, h_n = rnn(x) 后：

  1. output

  • 就是 最后一层（第 2 层）的输出 out₂

python 复制代码 
output.shape = (4, 6, 8)
  • 用途：做序列标注任务（如 NER、POS 标注），对每个词预测标签
  1. h_n（final hidden state）

  • 包含 每一层最后一个时间步的隐藏状态

python 复制代码 
h_n.shape = (3, 4, 8)
# 第0维：3层 → [layer0_final_h, layer1_final_h, layer2_final_h]
# 第1维：4个句子
# 第2维：8维隐藏状态

  • 提取整句表示（用于文本分类）：

    python 复制代码 
    sentence_vector = h_n[-1]  # 取最后一层 → shape: (4, 8)

🔍 五、验证：查看各层权重形状（证明维度自动匹配）

python 复制代码 
print("第0层 weight_ih_l0:", rnn.weight_ih_l0.shape)  # torch.Size([8, 10])
print("第1层 weight_ih_l1:", rnn.weight_ih_l1.shape)  # torch.Size([8, 8]) ← 关键！
print("第2层 weight_ih_l2:", rnn.weight_ih_l2.shape)  # torch.Size([8, 8])

✅ 第 1、2 层的输入权重都是 (8, 8)，说明它们的输入维度确实是 8，和上一层的输出匹配！

🧪 六、完整可运行代码（带注释）

python 复制代码 
import torch
import torch.nn as nn

# === 超参数（全不同）===
batch_size = 4      # 4个句子
seq_len = 6         # 每句6个词
input_size = 10     # 词向量10维
hidden_size = 8     # 隐藏状态8维
num_layers = 3      # 3层RNN

# === 构建模型 ===
rnn = nn.RNN(
    input_size=input_size,
    hidden_size=hidden_size,
    num_layers=num_layers,
    batch_first=True
)

# === 模拟输入 ===
x = torch.randn(batch_size, seq_len, input_size)
print("输入 x shape:", x.shape)  # (4, 6, 10)

# === 前向传播 ===
output, h_n = rnn(x)

print("\n最终 output shape:", output.shape)   # (4, 6, 8)
print("最终 h_n shape:", h_n.shape)         # (3, 4, 8)

# === 验证各层权重维度 ===
print("\n各层输入权重形状:")
print("Layer 0 (weight_ih_l0):", rnn.weight_ih_l0.shape)  # (8, 10)
print("Layer 1 (weight_ih_l1):", rnn.weight_ih_l1.shape)  # (8, 8)
print("Layer 2 (weight_ih_l2):", rnn.weight_ih_l2.shape)  # (8, 8)

输出：

复制代码 
输入 x shape: torch.Size([4, 6, 10])

最终 output shape: torch.Size([4, 6, 8])
最终 h_n shape: torch.Size([3, 4, 8])

各层输入权重形状:
Layer 0 (weight_ih_l0): torch.Size([8, 10])
Layer 1 (weight_ih_l1): torch.Size([8, 8])
Layer 2 (weight_ih_l2): torch.Size([8, 8])

✅ 一切维度对齐，无任何冲突！

🧠 七、关键总结（一句话记住）

在 nn.RNN(..., num_layers=N) 中：

  • 第 0 层 的输入维度 = input_size
  • 第 1 ~ N-1 层 的输入维度 = hidden_size
  • PyTorch 自动为每层创建匹配的权重矩阵，你无需手动处理维度衔接

📌 附：LSTM / GRU 是否相同？

✅ 完全相同！

例如：

python 复制代码 
lstm = nn.LSTM(input_size=10, hidden_size=8, num_layers=3, batch_first=True)
  • 第 0 层输入：(4,6,10) → 权重 (8,10)
  • 第 1、2 层输入：(4,6,8) → 权重 (8,8)
  • 返回 (output, (h_n, c_n))，其中 h_n.shape = (3,4,8)

希望这份维度全不同、逐层拆解、带验证代码 的解释，能让你对多层 RNN 的数据流彻底、永久地理解清楚！

27、RNN - API 进阶使用

一、nn.RNN 的完整参数详解

python 复制代码 
torch.nn.RNN(
    input_size,          # 必须 | int | 每个时间步输入特征的维度（如词向量维度）
    hidden_size,         # 必须 | int | 隐藏状态的维度，也是每层输出的特征数
    num_layers=1,        # 可选 | int | RNN 堆叠层数，默认 1；>1 时可在层间加 dropout
    nonlinearity='tanh', # 可选 | str | 激活函数，仅支持 'tanh' 或 'relu'；仅在单层单向时生效，通常保持默认
    bias=True,           # 可选 | bool | 是否使用偏置项；默认 True，一般不修改
    batch_first=False,   # 可选 | bool | 若为 True，输入/输出形状为 (batch, seq, feature)；NLP 中常设为 True
    dropout=0.0,         # 可选 | float | 层间 dropout 概率（仅作用于非最后一层）；仅当 num_layers > 1 时生效
    bidirectional=False, # 可选 | bool | 是否使用双向 RNN；若为 True，输出维度变为 2 * hidden_size
    device=None,        # 可选 | torch.device | 指定模块所在设备（如 'cpu' 或 'cuda'）；通常用 .to(device) 设置
    dtype=None           # 可选 | torch.dtype | 指定参数数据类型（如 torch.float32）；通常保持默认
)
  1. input_size: int
  • 作用：每个时间步输入向量的维度。
  • 示例 ：
    • 词嵌入维度为 300 → input_size=300
    • 时间序列每步有 5 个特征 → input_size=5
  • 必须匹配：输入张量的最后一维。
  1. hidden_size: int
  • 作用：RNN 隐藏状态的维度，也是每一层输出的特征数。
  • 注意 ：
    • 若 bidirectional=True，最终输出和最后一层隐藏状态的维度为 2 * hidden_size；
    • 但 h_n 中每个方向仍单独保存为 hidden_size。
  1. num_layers: int = 1
  • 作用：堆叠的 RNN 层数。
  • 行为 ：
    • 第 1 层接收原始输入；
    • 第 2 层接收第 1 层所有时间步的输出作为输入；
    • 所有层都处理整个序列（不是只处理一个时间步）。
  • 典型值：1~3。层数越多，模型越深，但也更容易梯度消失。
  1. nonlinearity: str = 'tanh'
  • 可选值 ：'tanh' 或 'relu'
  • 限制 ：
    • 仅支持单层、单向 RNN（即 num_layers == 1 且 bidirectional == False）；
    • 即便如此，在某些 PyTorch 版本或 CUDA 环境下，CUDNN 后端可能不支持 ReLU，导致回退到 CPU 或报错；
  • 建议 ：保持默认 'tanh'，除非明确需要且在 CPU 上调试。
  1. bias: bool = True
  • 作用：是否启用偏置项。
  • 影响 ：若设为 False，则不创建 bias_ih 和 bias_hh 参数。
  • 通常保留为 True。
  1. batch_first: bool = False ⭐⭐⭐（重点！）

  • 决定输入/输出张量的布局：

    batch_first 输入 x 形状 输出 output 形状
    False（默认） (seq_len, batch, input_size) (seq_len, batch, output_size)
    True (batch, seq_len, input_size) (batch, seq_len, output_size)

  • 推荐：

    • NLP 任务中通常设为 True，便于与 DataLoader 输出对齐；
    • 时间序列或传统任务可保留 False。

💡 注意：h_0 和 h_n 的形状不受 batch_first 影响！

  1. dropout: float = 0.0
  • 作用 ：在非最后一层的输出上应用 dropout。
  • 生效条件 ：仅当 num_layers > 1 时有效。
  • 机制 ：
    • 对第 0 层到第 num_layers-2 层的输出做 dropout；
    • 最后一层（num_layers-1）不做 dropout。
  • 典型值：0.2 ~ 0.5
  1. bidirectional: bool = False 【 bidirectional adj.双向的 】
  • 作用：是否使用双向 RNN。
  • 效果 ：
    • 每层会运行两个独立的 RNN：一个正向处理序列，一个反向处理；
    • 最终输出会在隐藏维度上拼接，因此输出特征维度变为 2 * hidden_size；
    • 参数数量翻倍（因为有两套权重）。
  1. device / dtype
  • 用于指定模块的设备（CPU/GPU）和数据类型（如 torch.float32）。
  • 通常通过 .to(device) 设置，无需在初始化时指定。

二、输入张量 input 的形状要求

标准格式（三维张量）：

python 复制代码 
# batch_first=False（默认）
input: (L, N, H_in)

# batch_first=True
input: (N, L, H_in)
  • L = sequence length（序列长度）
  • N = batch size（批次大小）
  • H_in = input_size

示例：

python 复制代码 
# 场景：3 个句子，最长 5 个词，词向量维度 100
x = torch.randn(3, 5, 100)  # (batch, seq, embed)

rnn = nn.RNN(100, 64, batch_first=True)
output, h_n = rnn(x)

⚠️ 重要 ：nn.RNN 不会自动跳过 padding 位置 ！如果你的 batch 中包含不同长度的序列，必须使用 pack_padded_sequence + pad_packed_sequence，否则 padding 会被当作真实数据参与计算，严重影响结果。

三、初始隐藏状态 h_0（可选输入）

形状规则（与 batch_first 无关！）：

python 复制代码 
h_0: (num_directions * num_layers, N, hidden_size)
  • num_directions = 2 if bidirectional else 1
  • N = batch size

构造示例：

单向单层：

python 复制代码 
h_0 = torch.zeros(1, batch, hidden_size)

双向双层：

python 复制代码 
h_0 = torch.zeros(4, batch, hidden_size)  # 2 directions × 2 layers

传入方式：

python 复制代码 
output, h_n = rnn(x, h_0=h_0)

默认行为：

  • 若不传 h_0，PyTorch 自动初始化为全 0 张量。

实用技巧：

  • 在语言模型中跨 batch 传递状态：

    python 复制代码 
    h = h.detach()  # 断开历史计算图
output, h = rnn(x, h)

四、返回值详解：output 与 h_n

  1. output
  • 含义 ：最后一层 在每个时间步的隐藏状态。
  • 形状 ：
    • batch_first=False → (L, N, output_size)
    • batch_first=True → (N, L, output_size)
    • 其中 output_size = hidden_size（单向）或 2 * hidden_size（双向）

✅ 用途：

  • 序列标注（NER、POS）→ 对每个位置分类
  • Encoder 输出 → 供 Attention 或 Decoder 使用
  1. h_n
  • 含义 ：每一层 在最后一个时间步的隐藏状态（正向/反向分开存储）。
  • 形状 ：(num_directions * num_layers, N, hidden_size) ← 固定格式，不受 batch_first 影响

✅ 用途：

  • 文本分类 → 用最后隐藏状态代表整句
  • 状态传递 → 作为下一个 RNN 的初始状态

如何提取有用信息？

情况1：单向 RNN（bidirectional=False）

python 复制代码 
# 取最后一层的最终隐藏状态
final_hidden = h_n[-1]  # (N, hidden_size)

情况2：双向 RNN（bidirectional=True，单层）

python 复制代码 
# h_n: (2, N, hidden_size)
forward_h = h_n[0]   # (N, hidden_size)
backward_h = h_n[1]  # (N, hidden_size)
combined = torch.cat([forward_h, backward_h], dim=1)  # (N, 2*hidden_size)

情况3：多层双向 RNN（num_layers=2, bidirectional=True）

python 复制代码 
# h_n: (4, N, hidden_size)
# 顺序为：[layer0_forward, layer0_backward, layer1_forward, layer1_backward]

last_forward = h_n[-2]  # layer1 forward
last_backward = h_n[-1] # layer1 backward
combined = torch.cat([last_forward, last_backward], dim=1)

📌 排列顺序是：按层优先，每层内先 forward 后 backward 。

因此，最后一层的前向状态是 h_n[-2]，后向是 h_n[-1]。

五、完整代码示例（覆盖各种场景）

示例1：最简使用（单向、单层、batch_first=True）

python 复制代码 
import torch
import torch.nn as nn

rnn = nn.RNN(10, 20, batch_first=True)
x = torch.randn(4, 6, 10)  # batch=4, seq=6, input=10

output, h_n = rnn(x)
print("output:", output.shape)  # (4, 6, 20)
print("h_n:", h_n.shape)        # (1, 4, 20)

# 用于分类：取最后一个时间步的隐藏状态
final_hidden = h_n.squeeze(0)  # (4, 20)
logits = nn.Linear(20, 2)(final_hidden)

示例2：双向 RNN 用于文本分类

python 复制代码 
rnn = nn.RNN(100, 64, bidirectional=True, batch_first=True)
x = torch.randn(8, 12, 100)  # 8 sentences, max_len=12

output, h_n = rnn(x)
# h_n: (2, 8, 64)

forward_h, backward_h = h_n[0], h_n[1]
final_repr = torch.cat([forward_h, backward_h], dim=1)  # (8, 128)

classifier = nn.Linear(128, 2)
logits = classifier(final_repr)

示例3：多层 RNN + Dropout

python 复制代码 
rnn = nn.RNN(
    input_size=50,
    hidden_size=128,
    num_layers=3,
    dropout=0.3,
    batch_first=True
)
x = torch.randn(5, 10, 50)

output, h_n = rnn(x)
print(h_n.shape)  # (3, 5, 128)

# 取最后一层
final_hidden = h_n[-1]
print(final_hidden.shape)   # (5, 128)

示例4：手动传入初始隐藏状态

python 复制代码 
batch, seq, in_dim = 2, 4, 10
hidden_size = 16
num_layers = 2
bidirectional = True

rnn = nn.RNN(in_dim, hidden_size, num_layers, bidirectional=bidirectional, batch_first=True)

x = torch.randn(batch, seq, in_dim)
h0 = torch.randn(4, batch, hidden_size)  # 2 directions × 2 layers

output, hn = rnn(x, h0)
print(hn.shape)  # (4, 2, 16)

示例5：与变长序列配合（使用 pack/pad）

python 复制代码 
from torch.nn.utils.rnn import pad_sequence, pack_padded_sequence, pad_packed_sequence

# 假设有两个句子，长度分别为 5 和 3
seqs = [torch.randn(5, 10), torch.randn(3, 10)]
lengths = torch.tensor([5, 3])

# padding
padded = pad_sequence(seqs, batch_first=True)  # (2, 5, 10)

# 排序（pack 要求降序）
sorted_lengths, idx = lengths.sort(descending=True)
padded = padded[idx]

# pack
packed = pack_padded_sequence(padded, sorted_lengths, batch_first=True)

# RNN
rnn = nn.RNN(10, 20, batch_first=True)
packed_output, h_n = rnn(packed)

# 解包（如果需要 output）
output, out_lengths = pad_packed_sequence(packed_output, batch_first=True)

这样可以避免 padding 部分参与计算，提升效率和精度。

六、常见错误与解决方案

错误信息 原因 修复方法
RuntimeError: Expected hidden size (1, 3, 20) but got (1, 2, 20) h_0 的 batch 维度与输入不一致 确保 h_0.shape[1] == input.shape[0 if batch_first else 1]
output has shape (5, 3, 20) but expected (5, 3, 40) 忘了 bidirectional=True 会让输出翻倍 检查是否设置了 bidirectional，并调整后续层输入维度
Expected tensor with dim 3, got 2 输入不是三维张量 确保输入是 (L,N,H) 或 (N,L,H)
CUDA error: device-side assert triggered 序列长度 ≤ 0 或索引越界 检查 lengths 是否全 > 0，且 ≤ max_seq_len
All input tensors must be on the same device x 和 h_0 设备不一致 调用 .to(device) 统一设备

七、与 LSTM / GRU 的 API 差异（仅接口层面）

特性 RNN LSTM GRU
初始化参数 相同 相同 相同
输入形状 相同 相同 相同
h_0 形状 (num_dirs * L, N, H) (num_dirs * L, N, H) (num_dirs * L, N, H)
返回值数量 2 (output, h_n) 2 (output, (h_n, c_n)) 2 (output, h_n)
是否需要 c_0 否 是（可选） 否

所以：除了 LSTM 多一个 cell state，其他用法几乎一致！

八、总结：使用 nn.RNN 的 checklist

✅ 确定 input_size 和 hidden_size

✅ 决定是否 batch_first=True（推荐 True）

✅ 根据任务选择 num_layers（1~3）和 bidirectional（分类常用双向）

✅ 构造输入为三维张量

✅ 理解 output 用于序列任务，h_n 用于分类/状态传递

✅ 双向时记得拼接 h_n[0] 和 h_n[1]

✅ 多层时 h_n[-1] 是最后一层（单向）或 h_n[-2]/h_n[-1]（双向）

✅ 变长序列必须用 pack_padded_sequence

✅ 如果使用 GPU，确保所有张量（包括 h_0）都在同一设备上

28、PyTorch里输入到底有几个------1个 or 2个

聚焦于：

PyTorch 中 nn.RNN 的前向调用（forward call）需要传入几个张量作为输入？这和"每个时间步有两个输入"有什么关系？

答案是：PyTorch 的接口设计是对理论 RNN 的批量（batched）、序列化（sequential）封装，输入张量个数 ≠ 单步计算的输入变量个数，但二者在逻辑上完全一致。

下面我们一步步拆解。

一、PyTorch 中 nn.RNN 的标准调用方式

python 复制代码 
import torch
import torch.nn as nn

rnn = nn.RNN(input_size=10, hidden_size=20, batch_first=True)

# 输入序列: batch_size=32, 序列长度=15, 每个token维度=10
x = torch.randn(32, 15, 10)          # shape: (B, T, D_in)

# 初始隐藏状态（可选）
h0 = torch.zeros(1, 32, 20)         # shape: (num_directions * num_layers, N, hidden_size)

# 前向传播
output, hn = rnn(x, h0)

关键点：

  • rnn(x, h0) 接收 两个张量参数 ：
    1. x：整个输入序列
    2. h0：初始隐藏状态（可选；若不传，默认为全零）

✅ 所以，从 PyTorch 函数调用角度看，nn.RNN 的输入是 2 个张量。

二、这两个输入张量对应什么？

PyTorch 输入 对应理论概念 说明
x (shape: (B, T, D_in)) { x 1 , x 2 , . . . , x T } \{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_T\} {x1,x2,...,xT} 包含了所有时间步的外部输入，一次性传入
h0 (shape: (num_directions * num_layers, B, D_hid)) h 0 \mathbf{h}_0 h0 初始隐藏状态（单层时 L=1）

注意：

  • x 不是单个 x t \mathbf{x}_t xt，而是整个序列打包成一个张量
  • h0 就是理论中的 h 0 \mathbf{h}_0 h0，只在 t=1 时使用

三、PyTorch 内部做了什么？（自动展开时间步）

虽然你只传了两个张量，但 nn.RNN 内部会自动按时间步循环，对每个 t 执行：

python 复制代码 
# 伪代码（简化版，忽略 batch 和 layer 维度）
h_prev = h0[0]  # 初始状态
for t in range(T):
    x_t = x[:, t, :]                     # 取出第 t 步输入
    h_t = tanh(W_xh @ x_t + W_hh @ h_prev + b_h)
    output[:, t, :] = h_t
    h_prev = h_t

在这个循环中，每一步的计算仍然严格依赖两个东西：

  1. 当前 token x_t
  2. 上一状态 h_prev

✅ 这和我们之前说的"每个时间步有两个输入 "完全一致！

四、对比总结：理论 vs PyTorch

视角 "输入"的含义 输入个数 说明
理论（单步、单样本） 计算 h t h_t ht 所需的变量 2 个 ： x t x_t xt, h t − 1 h_{t-1} ht−1 微观计算单元
PyTorch（整体、批量） 用户调用 RNN 层时传入的张量 2 个张量 ： input_seq, initial_hidden 宏观接口封装

🔔 关键理解 ：

PyTorch 把"所有 x t x_t xt"打包成一个张量 x，把"初始 h 0 h_0 h0"作为一个张量 h0，

从而用两个张量完成了对"T 个时间步 × 每步两个输入"的高效表达。

五、如果我不传 h0 呢？

python 复制代码 
output, hn = rnn(x)  # 不传 h0
  • PyTorch 会自动创建一个全零张量 作为 h0
  • 这对应理论中的 h 0 = 0 \mathbf{h}_0 = \mathbf{0} h0=0
  • 所以输入张量个数变为 1 个（只有 x），但内部逻辑不变

💡 这类似于函数有默认参数：def rnn(x, h0=None)。

六、常见误区澄清

❌ 误区1："PyTorch RNN 每步接收三个输入"

→ 错。用户只传两个张量，内部每步计算仍只用两个变量。

❌ 误区2："x 是一个输入，h0 是第二个，所以总共两个输入，和理论一致"

→ 基本正确，但要明确：

  • x 代表 T 个 x t x_t xt
  • h0 代表 1 个 h 0 h_0 h0
  • 总共参与计算的"输入变量实例"其实是 T + 1 个 （T 个 x t x_t xt + 1 个 h 0 h_0 h0），
  • 但接口张量数量是 2 个。

✅ 正确认知：

PyTorch 的两个输入张量，是对经典 RNN 理论中"序列输入 + 初始状态"的工程实现，二者在数学和计算逻辑上完全等价。

七、终极回答

经典 RNN 在 PyTorch 代码中的输入张量个数是：1 个或 2 个

  • 如果提供初始隐藏状态：2 个张量 （input_seq, h0）
  • 如果不提供：1 个张量 （input_seq，h0 自动设为零）
    这与理论中"每个时间步有两个输入（ x t x_t xt 和 h t − 1 h_{t-1} ht−1）"并不矛盾 ，

因为 PyTorch 的接口是对整个序列和初始条件的批量封装 ，

而内部循环依然严格遵循经典 RNN 的每步双输入机制。

29、代码：

python 复制代码 
import torch
import torch.nn as nn

torch.manual_seed(66)

x = torch.randn(2, 3, 5)   # 2个句子, 每个句子3个词, 每个词是5维词向量

rnn = nn.RNN(input_size=5, hidden_size=4, num_layers=2, batch_first=True)

output, hidden = rnn(x)
print(output.shape)     # (2, 3, 4)
print(hidden.shape)     # (2, 2, 4)
相关推荐
童话名剑3 小时前
情感分类与词嵌入除偏（吴恩达深度学习笔记）
笔记·深度学习·分类
咋吃都不胖lyh3 小时前
CLIP 不是一个 “自主判断图像内容” 的图像分类模型，而是一个 “图文语义相似度匹配模型”—
人工智能·深度学习·机器学习
咚咚王者5 小时前
人工智能之核心技术 深度学习 第七章 扩散模型（Diffusion Models）
人工智能·深度学习
逄逄不是胖胖5 小时前
《动手学深度学习》-60translate实现
人工智能·python·深度学习
koo3646 小时前
pytorch深度学习笔记19
pytorch·笔记·深度学习
哥布林学者7 小时前
吴恩达深度学习课程五：自然语言处理 第三周：序列模型与注意力机制（三）注意力机制
深度学习·ai
A先生的AI之旅7 小时前
2026-1-30 LingBot-VA解读
人工智能·pytorch·python·深度学习·神经网络
Learn Beyond Limits7 小时前
文献阅读：A Probabilistic U-Net for Segmentation of Ambiguous Images
论文阅读·人工智能·深度学习·算法·机器学习·计算机视觉·ai
下午写HelloWorld8 小时前
差分隐私深度学习（DP-DL）简要理解
人工智能·深度学习
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Clawdbot 中文汉化版 接入微信、飞书04OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书052026美赛A题智能手机电池续航时间预测的连续时间数学模型06UV安装并设置国内源07Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services08Claude Code Skills 实用使用手册09Linux下V2Ray安装配置指南10在Trae中使用Pencil MCP