MATLAB中LASSO方法的特征矩阵优化与特征选择实现

一、LASSO方法的核心原理与MATLAB实现基础

LASSO（Least Absolute Shrinkage and Selection Operator）通过L1正则化实现特征选择，其目标函数为：

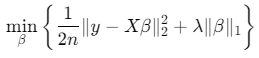
其中，λ控制正则化强度， $∥β∥$ 1为L1范数（系数绝对值之和）。MATLAB通过lasso函数实现该算法，支持交叉验证自动选择最优λ。

关键特性：

稀疏性：自动将不重要特征的系数压缩至0。
特征选择：非零系数对应的特征即为重要特征。
线性模型兼容性：适用于线性回归、逻辑回归等场景。

二、MATLAB实现LASSO特征选择的完整流程

1. 数据预处理

标准化：消除量纲差异（LASSO对特征尺度敏感）。
缺失值处理：删除或插补缺失值。
数据划分：分为训练集与测试集。

matlab 复制代码

% 示例：加载数据并标准化
load('data.mat'); % 假设数据包含特征矩阵X和标签y
X = normalize(X); % 标准化
y = y(:); % 确保列向量
cv = cvpartition(size(X,1),'HoldOut',0.3); % 70%训练，30%测试
X_train = X(training(cv),:);
y_train = y(training(cv));
X_test = X(test(cv),:);
y_test = y(test(cv));

2. 模型训练与参数调优

交叉验证：通过K折交叉验证选择最优λ。
弹性网络扩展 ：结合L1和L2正则化（Alpha参数控制混合比例）。

matlab 复制代码

% 基本LASSO回归（线性模型）
[B, FitInfo] = lasso(X_train, y_train, 'CV', 10, 'Alpha', 1);

% 广义线性模型（如逻辑回归）
[B_logit, FitInfo_logit] = lassoglm(X_train, y_train, 'binomial', 'Link', 'logit', 'CV', 10);

3. 特征筛选

最优λ选择 ：根据交叉验证误差最小（IndexMinMSE）或1SE规则（Index1SE）。
非零系数提取：筛选出非零系数对应的特征。

matlab 复制代码

% 选择最小MSE对应的λ
lambda_min = FitInfo.IndexMinMSE;
coef_min = B(:, lambda_min);

% 选择1SE规则对应的λ（更稀疏）
lambda_1se = FitInfo.Index1SE;
coef_1se = B(:, lambda_1se);

% 提取非零特征索引
selected_features_min = find(coef_min ~= 0);
selected_features_1se = find(coef_1se ~= 0);

4. 模型评估

训练集与测试集预测：验证模型性能。
可视化分析：绘制系数路径与交叉验证误差曲线。

matlab 复制代码

% 测试集预测（线性回归）
y_pred = [ones(size(X_test,1),1) X_test] * [coef_min(1); coef_min(2:end)];

% 计算均方误差（MSE）
mse = mean((y_test - y_pred).^2);
disp(['Test MSE: ', num2str(mse)]);

% 绘制系数路径
lassoPlot(B, FitInfo, 'PlotType', 'Lambda', 'XScale', 'log');
title('Coefficient Path vs Log(\lambda)');

三、关键参数与优化策略

1. 正则化参数λ选择

交叉验证 ：默认使用10折交叉验证，可通过CV参数调整折数。
1SE规则：选择比最小MSE对应的λ稍大的值，以增加模型稀疏性。

2. 弹性网络（Elastic Net）扩展

混合正则化 ：通过Alpha参数平衡L1（特征选择）与L2（共线性处理）。

matlab 复制代码

% Alpha=0.5表示L1和L2惩罚各占50%
[B_elastic, FitInfo_elastic] = lasso(X_train, y_train, 'Alpha', 0.5, 'CV', 10);

3. 多模型支持

广义线性模型 ：支持逻辑回归、泊松回归等，通过lassoglm函数实现。
matlab 复制代码
```
% 逻辑回归示例
[B_logit, FitInfo_logit] = lassoglm(X_train, y_train, 'binomial', 'Link', 'logit');
```

四、应用案例：高维基因表达数据分析

1. 数据背景

目标：从10,000个基因中筛选与疾病相关的关键基因。
数据特点：样本量小（n=100），特征数高（p=10,000）。

2. MATLAB实现步骤

matlab 复制代码

% 加载数据
load('gene_expression.mat'); % X: 100x10000, y: 100x1（0/1标签）

% 数据预处理
X = normalize(X);
cv = cvpartition(size(X,1),'KFold',10); % 10折交叉验证

% LASSO特征选择（逻辑回归）
[B, FitInfo] = lassoglm(X, y, 'binomial', 'Link', 'logit', 'CV', cv);

% 选择最优λ
lambda_min = FitInfo.IndexMinMSE;
selected_genes = find(B(:, lambda_min) ~= 0);

% 结果输出
disp(['Selected Genes: ', num2str(length(selected_genes))]);
disp('Top 5 Genes:');
disp(selected_genes(1:5));

3. 结果分析

特征重要性排序：根据系数绝对值排序。
模型性能评估：通过ROC曲线与AUC值验证分类效果。

参考代码 lasso方法对特征矩阵进行优化特征选择 www.youwenfan.com/contentcsq/53566.html

五、常见问题与解决方案

1. 过拟合问题

原因：高维数据中噪声特征过多。
解决：增加正则化强度（减小λ）或引入弹性网络。

2. 多重共线性

原因：特征间高度相关。
解决：使用弹性网络（Alpha < 1）或主成分分析（PCA）降维。

3. 计算效率低

优化：对稀疏矩阵使用lasso的'UseLARS'选项加速。
matlab 复制代码
```
[B, FitInfo] = lasso(X_train, y_train, 'UseLARS', true);
```

六、扩展应用与工具

实时特征选择 ：结合在线学习算法（如onlineLasso）处理流数据。
多模态数据融合：联合不同模态特征（如图像+文本）进行联合LASSO分析。
可视化工具 ：使用lassoPlot分析系数路径与交叉验证误差。

七、总结

MATLAB通过lasso和lassoglm函数提供了完整的LASSO特征选择解决方案，适用于高维数据建模、基因筛选、金融风险预测等场景。关键步骤包括数据标准化、交叉验证参数选择、特征筛选与模型评估。通过弹性网络扩展和多模型支持，可进一步提升模型鲁棒性与解释性。