数据结构：二叉树（Binary tree）

[2.二叉树（Binary tree）](#2.二叉树（Binary tree）)

1.树:描述数据一对多的关系的数据结构

2.节点:组成树形结构的单独的数据元素称为树形结构中的节点

1.根节点：只有后继没有前驱

2.分支节点：既有前驱又有后继，树形结中的分支节点最多有一个前驱，但是可以有多个后继

叶子节点：只有前驱没有后继

3.前驱(祖先):数据从哪里来

4.后继(子孙):数据对应后续的节点

5.度:前驱或者后继的个数

1.入度: 均为1

2.出度:后续节点的个数

6.根节点所在的位置称为第一层，每过一个节点，层数+1

7.节点的高度：距离该节点最远的叶子节点的距离

8.节点的深度：距离根节点的节点个数

9.树的高度 == 树的深度 == 树的层数

1.概念：一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

1.树形结构中每个节点最多有2个后继节点，称为二叉树

2.满二又树（特殊的完全二叉树）：所有的叶子节点都在同一层

3.空二叉树：集合为空时的二叉树

4.左孩子:二又树中节点左侧的子节点称为左孩子，也叫左节点

右孩子:二叉树中节点右侧的子节点称为右孩子，也叫右节点

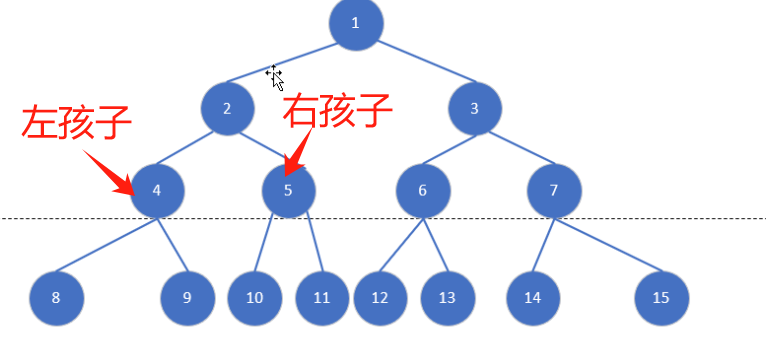4.完全二叉树：将二叉树所有节点展开后编号连续称为完全二叉树【记：编号连续，所以完全】

2.二叉树特性

1.第k层最多有:2^(k-1)个节点

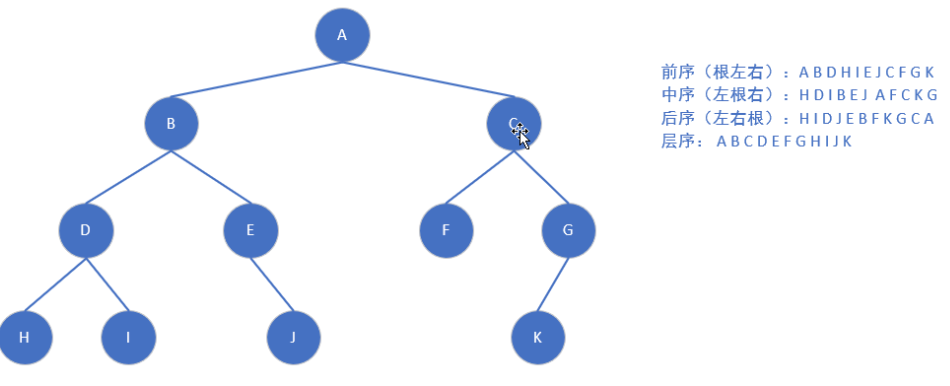
3.二叉树的遍历:树的遍历实质上是将二叉树的各个节点转换成为一个线性序列来表示

深度优先遍历（DFS）：

前序遍历：根左右------通常用于复制一棵树的结构。

中序遍历：左根右

后序遍历：左右根------通常用于先处理子节点再处理父节点的场景，如计算目录大小或释放二叉树内存。

注意：已知前序中序，可得二叉树，进而求得后续

已知中序后续，可得二叉树，进而求得前续

广度优先遍历（BFS）:

层序遍历:逐层从左到右遍历访问节点，这需要借助队列来实现
练习

4.应用：

许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。

主要应用 ：实现二叉搜索树进行高效查找排序、表达式求值、数据压缩（哈夫曼编码）等