一、逻辑回归核心概念
1.1 什么是逻辑回归?
逻辑回归(Logistic Regression)是一种分类算法(而非回归算法),核心目标是预测样本属于某一类别的概率,特别适用于二分类问题(如 "是否违约""是否患病"),也可扩展到多分类场景。
1.2 与线性回归的核心区别
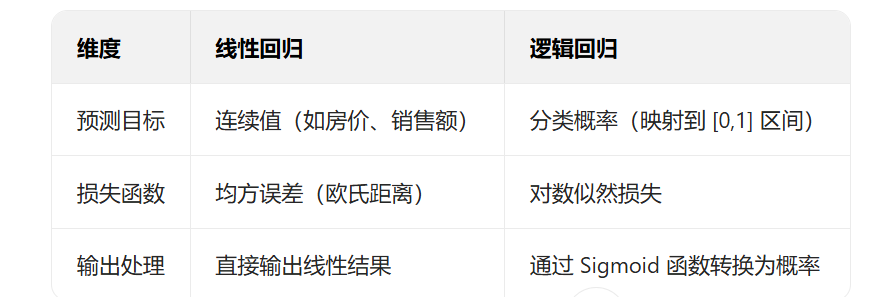
二、逻辑回归核心原理
2.1 Sigmoid 函数:从线性到概率的转换
逻辑回归的核心是通过 Sigmoid 函数,将线性回归的连续输出映射到 [0,1] 区间,从而表示 "属于正类" 的概率。
函数定义:
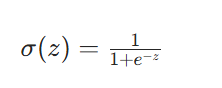
2.2 损失函数与优化
逻辑回归使用对数似然损失函数(也叫交叉熵损失),衡量模型预测概率与真实标签的偏差:
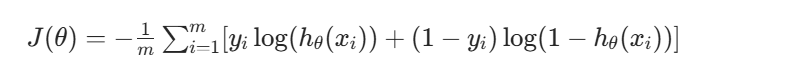
损失化函数:
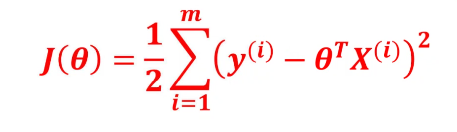
优化方法:梯度下降梯度下降的核心思想是 "沿损失函数下降方向调整参数",类比 "蒙眼下山找最低点",通过迭代更新参数 θ,最小化损失函数:

三、正则化技术:解决过拟合的核心手段
3.1 正则化的本质
正则化是在损失函数中加入权重惩罚项,强迫模型参数(权重)变小,降低模型复杂度,从而避免过拟合(模型 "死记硬背" 训练集,泛化能力差)。
3.2 两种常用正则化
正则化法则
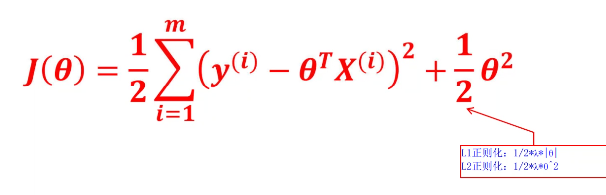
(1)L1 正则化:特征选择神器
惩罚项:
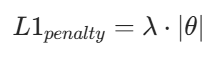
特点:会让部分权重直接变为 0,相当于自动筛选重要特征,适合高维数据(如电商用户特征、文本特征)。
(2)L2 正则化:最常用的权重衰减
惩罚项:
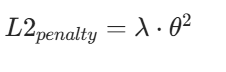
特点:让所有权重都变小且均匀,不会直接置 0,能有效降低模型复杂度,是工业界最常用的正则化方式(也叫 "权重衰减")。
3.3 正则化强度 C 的选择(核心实战)
在 sklearn 中,C是正则化强度 λ 的倒数(C=1/λ):
C 越小 → λ 越大 → 正则化越强 → 模型越简单(防止过拟合);
C 越大 → λ 越小 → 正则化越弱 → 模型越复杂(易过拟合)。
(1)手动选择思路(按业务目标优化)
如果业务核心目标是召回率(Recall)(如风控场景 "不漏掉坏样本"),步骤如下:
-
定义 C 的搜索范围:按对数尺度选取,覆盖强→弱正则化,如[0.01, 0.1, 1, 10, 100];
-
交叉验证评估:对每个 C 值做 5/10 折交叉验证,计算召回率平均值;
-
绘制 C-Recall 曲线:找到召回率峰值对应的 C 值(C 太小欠拟合、太大过拟合)。
(2)自动化选择:网格搜索 + 交叉验证(推荐)
通过代码自动遍历候选 C 值,结合交叉验证选择最优值,是工业界最稳健的方法:
python
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
# 1. 定义基础模型
model = LogisticRegression(penalty='l2', solver='liblinear', class_weight='balanced')
# 2. 定义C的搜索范围
param_grid = {'C': [0.01, 0.1, 1, 10, 100]}
# 3. 5折交叉验证,按召回率优化(可替换为accuracy/precision)
grid_search = GridSearchCV(model, param_grid, cv=5, scoring='recall')
grid_search.fit(X_train, y_train)
# 4. 输出最优参数
print("最佳正则化强度C:", grid_search.best_params_['C'])
print("最优模型召回率:", grid_search.best_score_)四、Sklearn 实战:逻辑回归参数配置
4.1 核心参数说明
python
from sklearn.linear_model import LogisticRegression
# 核心参数配置
model = LogisticRegression(
penalty='l2', # 正则化方式:l1/l2
C=1.0, # 正则化强度(越小正则化越强)
solver='liblinear', # 优化算法(关键!根据数据规模选择)
max_iter=100, # 最大迭代次数(确保模型收敛)
class_weight='balanced' # 处理类别不平衡(如正样本占1%,负样本占99%)
)4.2 优化算法(solver)选择
|-------|-----------|-------------|
| 场景 | 推荐 solver | 原理 |
| 小数据集 | liblinear | 坐标下降法(稳定) |
| 大数据集 | sag/saga | 随机平均梯度下降(快) |
| 多分类问题 | lbfgs | 拟牛顿法(支持多分类) |
五、过拟合 / 欠拟合与数据量不足的处理
5.1 过拟合 vs 欠拟合
|-----|---------------|-------------|
| 问题 | 表现 | 核心原因 |
| 欠拟合 | 训练集 / 测试集效果都差 | 模型太简单,没学到特征 |
| 过拟合 | 训练集好,测试集差 | 模型太复杂,过度拟合 |
5.2 过拟合解决方法
-
增加正则化强度:减小 C 值(如从 1→0.1),强迫模型简化;
-
交叉验证:将数据分成训练集 + 验证集 + 测试集,用验证集调参,测试集仅做最终评估;
常用 10 折交叉验证:将数据分 10 份,轮流用 9 份训练、1 份测试,取平均值评估,减少数据划分的随机性偏差;
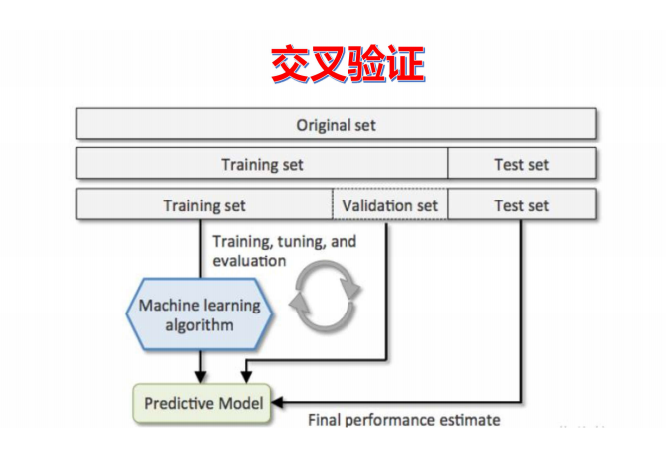
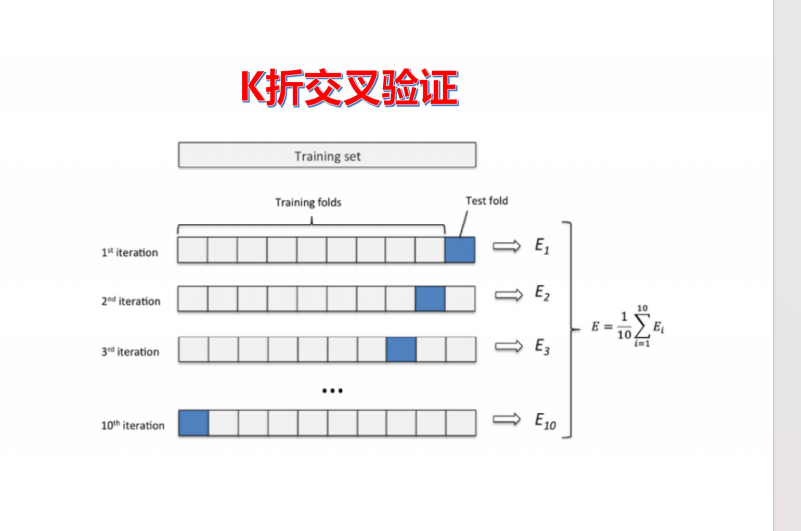
- 减少特征维度:删除冗余 / 噪声特征,降低模型复杂度。
5.3 数据量不足的处理
-
精简测试集:仅留 10% 数据做最终测试,90% 用于训练 + 交叉验证;
-
数据增强:对现有数据做轻微变换(如数值特征加噪声、类别特征重采样);
python
from sklearn.utils import resample
# 重采样增强数据(示例)
X_resampled, y_resampled = resample(X_train, y_train, n_samples=10000, random_state=42)3.结合强正则化:数据少易过拟合,选择更小的 C 值(如 0.01)。
六、完整实战代码
python
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, recall_score
from sklearn.preprocessing import StandardScaler
# 1. 数据准备(替换为你的数据路径)
data = pd.read_csv('your_data.csv')
X = data.drop('target', axis=1) # 特征
y = data['target'] # 标签(0/1)
# 2. 数据标准化(逻辑回归对特征尺度敏感,必须做!)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 3. 划分训练集(90%)和测试集(10%)
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.1, random_state=42 # 少留测试集,解决数据量不足
)
# 4. 网格搜索选择最优C值(按召回率优化)
param_grid = {'C': [0.01, 0.1, 1, 10, 100]}
base_model = LogisticRegression(penalty='l2', solver='liblinear', class_weight='balanced')
grid_search = GridSearchCV(base_model, param_grid, cv=10, scoring='recall')
grid_search.fit(X_train, y_train)
best_C = grid_search.best_params_['C']
# 5. 用最优C值训练最终模型
final_model = LogisticRegression(
penalty='l2',
C=best_C,
solver='liblinear',
class_weight='balanced',
max_iter=200
)
final_model.fit(X_train, y_train)
# 6. 模型评估
y_pred = final_model.predict(X_test)
print(f"最优C值: {best_C}")
print(f"测试集准确率: {accuracy_score(y_test, y_pred):.4f}")
print(f"测试集召回率: {recall_score(y_test, y_pred):.4f}")Sigmoid 函数是逻辑回归的核心,将线性输出转换为 [0,1] 区间的概率,是分类的基础;
正则化通过惩罚权重解决过拟合,L2 更常用,C 值越小正则化越强(需结合交叉验证选择);
实战关键:数据标准化、按业务目标(如召回率)调参、用交叉验证避免过拟合,小数据集需精简测试集 + 强正则化。