【深度学习教程——01_深度基石(Foundation)】04_分类问题怎么解？逻辑回归与交叉熵的由来

04_分类问题怎么解？逻辑回归与交叉熵的由来

本章目标：从"预测分数"跨越到"预测概率"。理解 Sigmoid 激活函数和 CrossEntropy 损失函数这对"黄金搭档"是如何诞生的。

📖 目录

从回归到分类：不仅是换个名字
Sigmoid：把线性值压弯
[为什么分类不用 MSE？](#为什么分类不用 MSE？)
[Cross Entropy：信息论的视角](#Cross Entropy：信息论的视角)
[实战：PyTorch 实现逻辑回归](#实战：PyTorch 实现逻辑回归)

1. 从回归到分类：不仅是换个名字

在前几章，我们解决的是回归 (Regression) 问题：预测一个连续的数值（如分数、房价）。
y ^ ∈ ( − ∞ , + ∞ ) \hat{y} \in (-\infty, +\infty) y^∈(−∞,+∞)

但在现实世界中，更多的是分类 (Classification) 问题：

这张图是猫(1)还是狗(0)？
这封邮件是垃圾邮件(1)还是正常邮件(0)？
y ∈ { 0 , 1 } y \in \{0, 1\} y∈{0,1}

如果我们直接用线性模型 y ^ = x ⋅ w + b \hat{y} = x \cdot w + b y^=x⋅w+b，输出可能是 2.5 2.5 2.5 甚至 − 100 -100 −100。这代表什么？概率不能超过 1，也不能小于 0。

我们需要一个"压缩机"，把线性输出强行压缩到 ( 0 , 1 ) (0, 1) (0,1) 之间。

2. Sigmoid：把线性值压弯

我们要找一个函数 σ ( z ) \sigma(z) σ(z)，满足：

当 z → + ∞ z \to +\infty z→+∞， σ ( z ) → 1 \sigma(z) \to 1 σ(z)→1
当 z → − ∞ z \to -\infty z→−∞， σ ( z ) → 0 \sigma(z) \to 0 σ(z)→0

这个函数就是 Logistic Sigmoid ：
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1

其中 z = x ⋅ w + b z = x \cdot w + b z=x⋅w+b 称为 Logits。

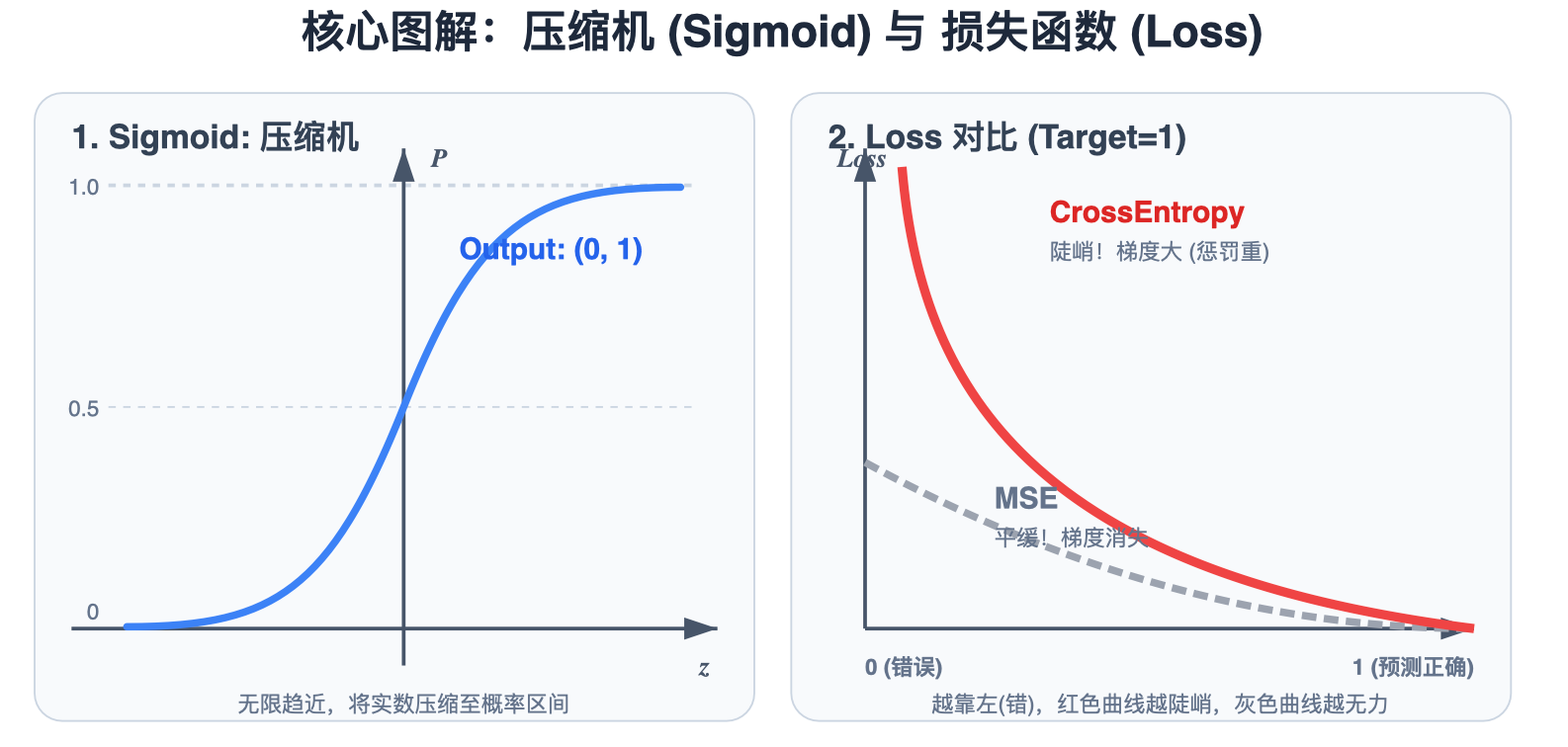
请看图中的 左图 (Sigmoid: 压缩机) ：Sigmoid 函数平滑地将任意实数 z z z 压缩成概率值 P ∈ ( 0 , 1 ) P \in (0, 1) P∈(0,1)。

P ( y = 1 ) = σ ( z ) P(y=1) = \sigma(z) P(y=1)=σ(z)
P ( y = 0 ) = 1 − σ ( z ) P(y=0) = 1 - \sigma(z) P(y=0)=1−σ(z)

3. 为什么分类不用 MSE？

既然有了预测概率 y ^ \hat{y} y^ 和真实标签 y y y，我们能不能继续用 MSE 算 Loss？
L o s s = ( y ^ − y ) 2 = ( σ ( z ) − y ) 2 Loss = (\hat{y} - y)^2 = (\sigma(z) - y)^2 Loss=(y^−y)2=(σ(z)−y)2

答案是：可以用，但效果很差。

请看图中 右图 (Loss 对比) 的灰色虚线曲线 (MSE)：

假设真实标签 y = 1 y=1 y=1 (Target=1)。
当预测值 y ^ ≈ 0 \hat{y} \approx 0 y^≈0（错得离谱）时，MSE 的曲线非常平缓 (坡度缓)。
平缓这意味着梯度几乎为 0 。梯度消失 → \to → w 更新不动 → \to → 模型学不会。

这被称为 梯度消失 (Gradient Vanishing)。在分类问题中，MSE 是一个非凸函数，容易卡在局部最优解。

4. Cross Entropy：信息论的视角

为了解决 MSE 梯度小的问题，我们引入 交叉熵 (Cross Entropy) 。它的核心思想是：如果预测错了，我要给你一个极其严厉的惩罚！

对于二分类，交叉熵公式为：
L o s s = − ( y ⋅ ln ⁡ y ^ + ( 1 − y ) ⋅ ln ⁡ ( 1 − y ^ ) ) Loss = -(y \cdot \ln\hat{y} + (1-y) \cdot \ln(1-\hat{y})) Loss=−(y⋅lny^+(1−y)⋅ln(1−y^))

当 y = 1 y=1 y=1 : L o s s = − ln ⁡ ( y ^ ) Loss = -\ln(\hat{y}) Loss=−ln(y^)。如果你预测 y ^ → 0 \hat{y} \to 0 y^→0 (错)， L o s s → + ∞ Loss \to +\infty Loss→+∞。
当 y = 0 y=0 y=0 : L o s s = − ln ⁡ ( 1 − y ^ ) Loss = -\ln(1-\hat{y}) Loss=−ln(1−y^)。如果你预测 y ^ → 1 \hat{y} \to 1 y^→1 (错)， L o s s → + ∞ Loss \to +\infty Loss→+∞。

请看图中 右图 (Loss 对比) 的红色实线曲线 (CrossEntropy)：

在预测错误时（ y ^ → 0 \hat{y} \to 0 y^→0，即 X 轴左侧），Loss 曲线极其陡峭。如图所示"梯度陡峭，惩罚严重"，这意味着梯度很大，模型会被"狠狠地踢一脚"，迅速修正参数。

结论：Sigmoid + CrossEntropy 是二分类的最佳拍档。

5. 实战：PyTorch 实现逻辑回归

PyTorch 提供了 torch.nn.BCELoss (Binary Cross Entropy) 和 torch.nn.BCEWithLogitsLoss（推荐）。

python 复制代码

import torch
import torch.nn as nn
import torch.nn.functional as F

# 1. 准备数据 (二分类)
# x_data: [Hours], y_data: [Fail=0, Pass=1]
x_data = torch.tensor([[1.0], [2.0], [3.0]], dtype=torch.float32)
y_data = torch.tensor([[0.0], [0.0], [1.0]], dtype=torch.float32)

# 2. 定义模型
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)  # w * x + b

    def forward(self, x):
        # 加上 Sigmoid 激活函数
        # linear(x) 输出的是 Logits
        return F.sigmoid(self.linear(x))

model = LogisticRegressionModel()

# 3. 损失函数
# BCELoss 要求输入必须是概率 (经过 Sigmoid)
criterion = torch.nn.BCELoss()

# 4. 优化器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 5. 训练循环
for epoch in range(1000):
    # Forward
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)

    # Backward
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 200 == 0:
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")

# 6. 测试
print("\n测试预测:")
hour_var = torch.tensor([[4.0]])
prob = model(hour_var).item()
print(f"学习 4 小时通过的概率: {prob:.4f} ({'>0.5 通过' if prob > 0.5 else '挂科'})")

关键点：BCEWithLogitsLoss

在工业界，我们通常不直接用 F.sigmoid + BCELoss，而是直接使用 BCEWithLogitsLoss。

它在内部将 Sigmoid 和 BCE 合并运算，利用 LogSumExp 技巧，数值稳定性更高 ，防止 log(0) 导致 NaN。

python 复制代码

# 更稳健的写法
class RobustModel(torch.nn.Module):
    def forward(self, x):
        return self.linear(x) # 不加 Sigmoid，直接输出 Logits

criterion = torch.nn.BCEWithLogitsLoss()

总结

这一章我们完成了从回归到分类的跃迁。

Sigmoid: 概率压缩机，把数值压到 0~1。
CrossEntropy: 对错误预测进行"指数级暴击"，解决梯度消失。
Visualization: 通过数学精确的双面板对比图，直观展示了 Sigmoid 激活函数的压缩特性，以及 MSE 和 CrossEntropy 在分类任务中的差异。

下一章预告 ：

数据量只有 3 个没什么了不起。如果是 3 万个呢？一次性把所有数据塞进 GPU 显存会爆炸。我们需要 Mini-Batch 训练。这就是下一章的核心 ------ 数据管道的设计模式。

➡️ 下一章：05_数据太多怎么吃？Mini-batch训练的设计模式