贪心-最长递增子序列

我帮你把这张笔记里的核心知识点整理成清晰的模块，方便你复习和记忆：

---

一、题目：最长递增子序列（LIS）

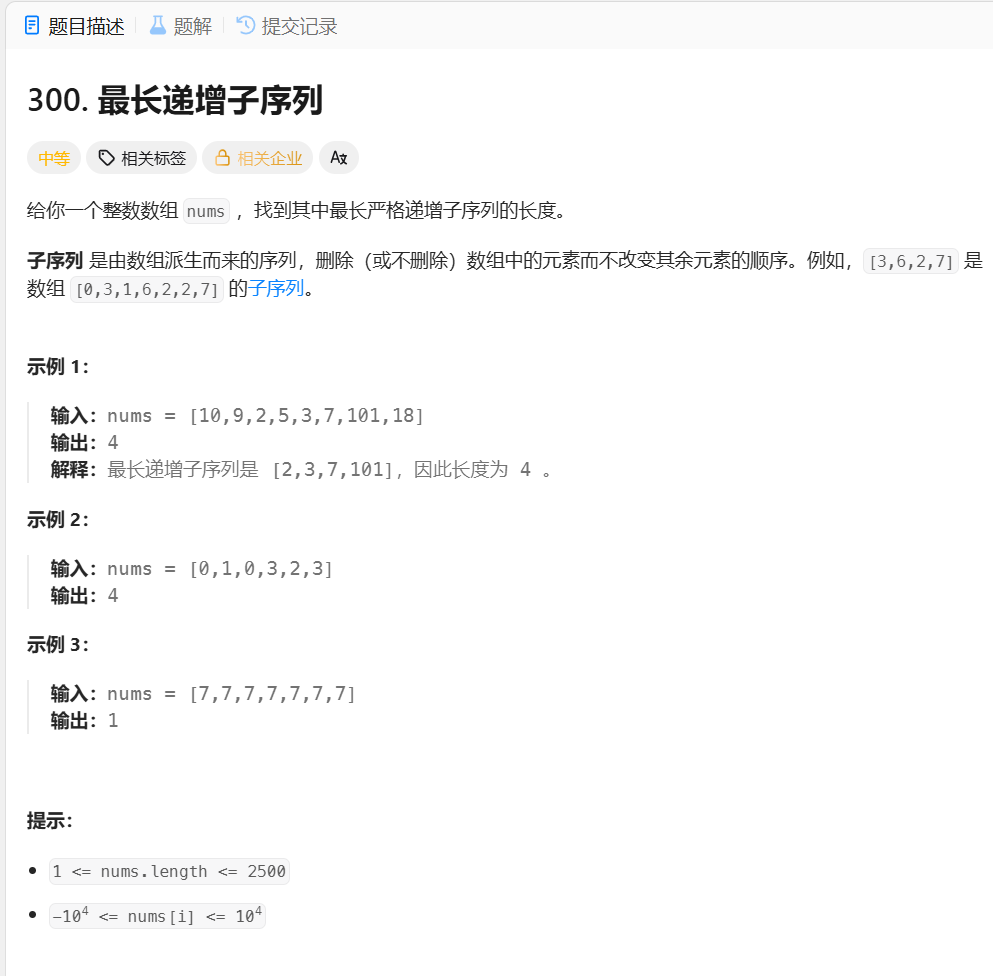
• 定义 ：子序列是从数组中删除（或不删除）元素且不改变剩余元素顺序得到的序列；题目要求是严格递增的子序列。
• 目标：找到数组中最长的严格递增子序列的长度。
• 示例 ：输入 [10,9,2,5,3,7,101,18] → 输出 4（对应子序列 [2,3,7,101]）。

---

二、算法1：动态规划（DP）解法

• 时间复杂度：O(n²)

• 状态表示 ：dp[i] 表示以第 i 个元素结尾的所有子序列中，最长递增子序列的长度。

• 状态转移方程 ：

  dp[i] = max(dp[j] + 1)  （其中 j < i 且 nums[j] < nums[i]）

• 核心思路 ：对每个位置 i，向前遍历所有 j < i，找到能让 dp[i] 最大的 dp[j]，加 1 即为当前位置的最长长度。

---

三、算法2：贪心 + 二分查找优化解法

• 时间复杂度：O(n log n)
• 贪心思想 ：
  1. 维护一个数组 tails，其中 tails[x] 表示所有长度为 x+1 的递增子序列中，最后一个元素的最小值。
  2. 核心逻辑：相同长度的子序列，最后一个元素越小，后续越容易接上更大的元素，从而形成更长的子序列。
• 二分查找的作用 ：
  对当前元素 nums[i]，在 tails 数组中找到第一个大于等于 nums[i] 的位置 ，并将该位置的值更新为 nums[i]；若 nums[i] 比 tails 所有元素都大，则直接追加到末尾。
• 最终结果 ：tails 数组的长度就是最长递增子序列的长度。
• 关键性质 ：tails 数组是严格递增的（可通过直接证明法验证），因此可以用二分查找高效定位。
• 边界情况 ：当 nums[i] > tails[-1] 时，直接追加到 tails 末尾。

---

四、辅助理解的例子

以数组 [7,3,8,4,7,2,14,13] 为例，tails 数组的变化过程：

1. 长度 1：[7] → 更新为 [3]（3 更小，更优）
2. 长度 2：[3,8] → 更新为 [3,4]（4 比 8 小，更优）
3. 长度 3：[3,4,7]
4. 长度 4：[3,4,7,14] → 更新为 [3,4,7,13]（13 比 14 小，更优）
   最终 tails 长度为 4，即最长递增子序列长度为 4。

---

五、注意事项

• 这是动态规划的经典题目，优化解法需要结合贪心和二分查找。
• 贪心优化的核心是关注子序列最后一个元素的最小值，而非子序列本身的具体内容。