LeetCode_二叉树1

珍珠是蚌的眼泪2026-02-03 12:21

二叉树

进阶二叉树算法题请点击LeetCode_二叉树2

1、二叉树思路总结

1.1 树的自顶向下和自底向上遍历

  1. 自顶向下
    前序遍历：先看当前节点的情况，再看当前节点的左子节点和右子节点的情况，然后层层向下，但是存在的问题是可能存在重复遍历的情况。
  2. 自底向上
    后序遍历：先看当前节点的左子节点和右子节点的情况，再看当前节点的情况，然后层层向上，不存在重复遍历，节省复杂度。典型题：平衡二叉树（力扣110）

1.2 深度和高度

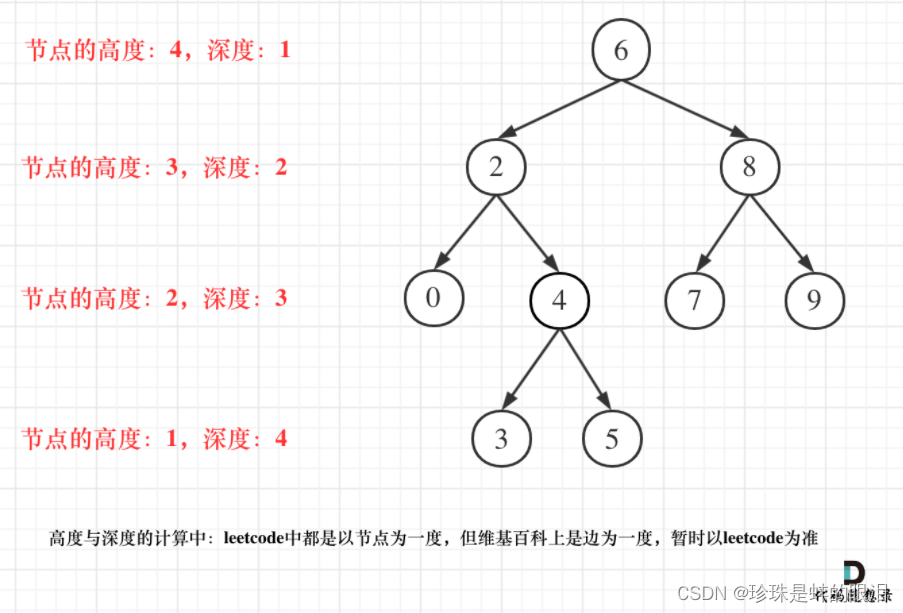
  1. 二叉树的高度和深度是等价的。
  2. 二叉树节点的深度 ：指从根节点到该节点的最长路径包含的节点个数。求深度：可以从上到下去查 所以需要前序遍历（中左右）。
    二叉树节点的高度：指从该节点到叶子节点的最长路径包含的节点个数。求高度：从下到上去查，所以只能后序遍历（左右中）。

1.3 递归函数有无返回值的判断

  1. 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（113.路径总和ii）
  2. 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （236. 二叉树的最近公共祖先）
  3. 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（路径总和112）

1.4 前中后序两两组合确定二叉树

  1. 前序和中序可以唯一确定一棵二叉树。
  2. 后序和中序可以唯一确定一棵二叉树。
  3. 前序和后序不能唯一确定一棵二叉树

1.5 递归函数有返回值时，如何区分搜索一条边还是搜索整个树

  1. 搜索一条边的写法(直接返回)
java 复制代码 
if(递归函数（root.left）) return;
if(递归函数（root.right）) return;
  1. 搜索整个树的写法（用left和right变量接住返回值，进行逻辑处理）
java 复制代码 
left = 递归函数（root.left）
right = 递归函数(root.right)
left 和 right 的逻辑处理

1.6 递归函数前加if

什么时候递归函数前面加if，什么时候不加if？一般情况来说：如果让空节点（空指针）进入递归，就不加if，如果不让空节点进入递归，就加if限制一下， 终止条件也会相应的调整。

2、二叉树的前序遍历（力扣144）

java 复制代码 
//1.递归
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        preOrder(root,list);
        return list;
    }

    public void preOrder(TreeNode root,List<Integer> list){
        if(root == null){
            return;
        }

        list.add(root.val);
        preOrder(root.left,list);
        preOrder(root.right,list);
    }
java 复制代码 
//2.迭代，利用栈
    public static List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        Deque<TreeNode> stack = new LinkedList<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            list.add(node.val);
            // 先右子结点入栈
            if(node.right != null){
                stack.push(node.right);
            }
            // 再左子结点入栈
            if(node.left != null){
                stack.push(node.left);
            }
        }
        return list;
    }

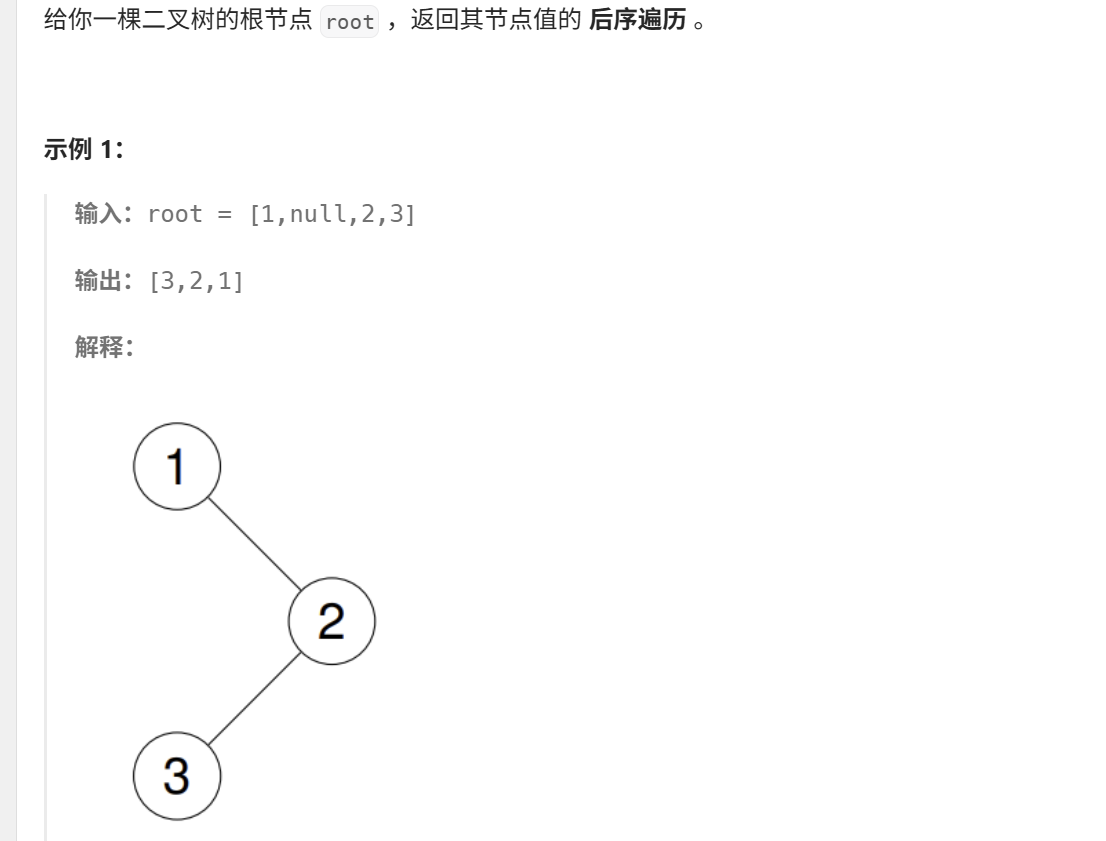
3、二叉树的后序遍历（力扣145）

java 复制代码 
//1.递归
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        postOrder(root,list);
        return list;
    }

    public void postOrder(TreeNode root,List<Integer> list){
        if(root == null){
            return;
        }

        postOrder(root.left,list42
        postOrder(root.right,list);
        list.add(root.val);
    }
java 复制代码 
//2.迭代（利用栈，多了一次反转）
    public List<Integer> postorderTraversal2(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        Deque<TreeNode> stack = new LinkedList<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            list.add(node.val);
            if(node.left != null){
                stack.push(node.left);
            }
            if(node.right != null){
                stack.push(node.right);
            }
        }
        
		// 此时顺序为根右左，反转即为：左右根
        Collections.reverse(list);
        return list;
    }
java 复制代码 
//3.迭代（利用栈，推荐使用）
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null) return list;

        Deque<TreeNode> stack = new LinkedList<>();
        //由于在某颗子树访问完成以后，接着就要回溯到其父节点去
        //因此可以用pre来记录访问历史，在回溯到父节点时，可以由此来判断，上一个访问的节点是否为右子结点
        TreeNode cur = root, pre = null;
        while(cur != null || !stack.isEmpty()){
        	// 沿着左子树一直到空为止
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            //从栈中弹出的节点，其左子树一定已经访问了
            cur = stack.pop();
            //如果没有右子树或者右子树已经访问完了，表示可以访问当前节点了
            if(cur.right == null || cur.right == pre){
                list.add(cur.val);
                //更新pre，记录上一个访问的节点
                pre = cur;
                //切记将cur置为空
                cur = null;
            }else{
                //如果右子树还没有访问，先访问右子树
                stack.push(cur);
                cur = cur.right;
            }
        }
        return list;
    }

4、二叉树的中序遍历（力扣94）

java 复制代码 
//1.递归
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        inOrder(root,list);
        return list;
    }

    public void inOrder(TreeNode root,List<Integer> list){
        if(root == null){
            return;
        }

        inOrder(root.left,list);
        list.add(root.val);
        inOrder(root.right,list);
    }
java 复制代码 
//2.迭代（利用栈）
    public List<Integer> inorderTraversal2(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        // 两种情况，要么左子树到底，要么弹栈
        while(cur != null || !stack.isEmpty()){
            //沿着左子树一直为空为止
            if(cur != null){
                stack.push(cur);
                cur = cur.left;
            }else{
                //开始往外弹栈
                cur = stack.pop();
                list.add(cur.val);
                //弹栈过程中考虑右子树
                cur = cur.right;
            }
        }
        return list;
    }

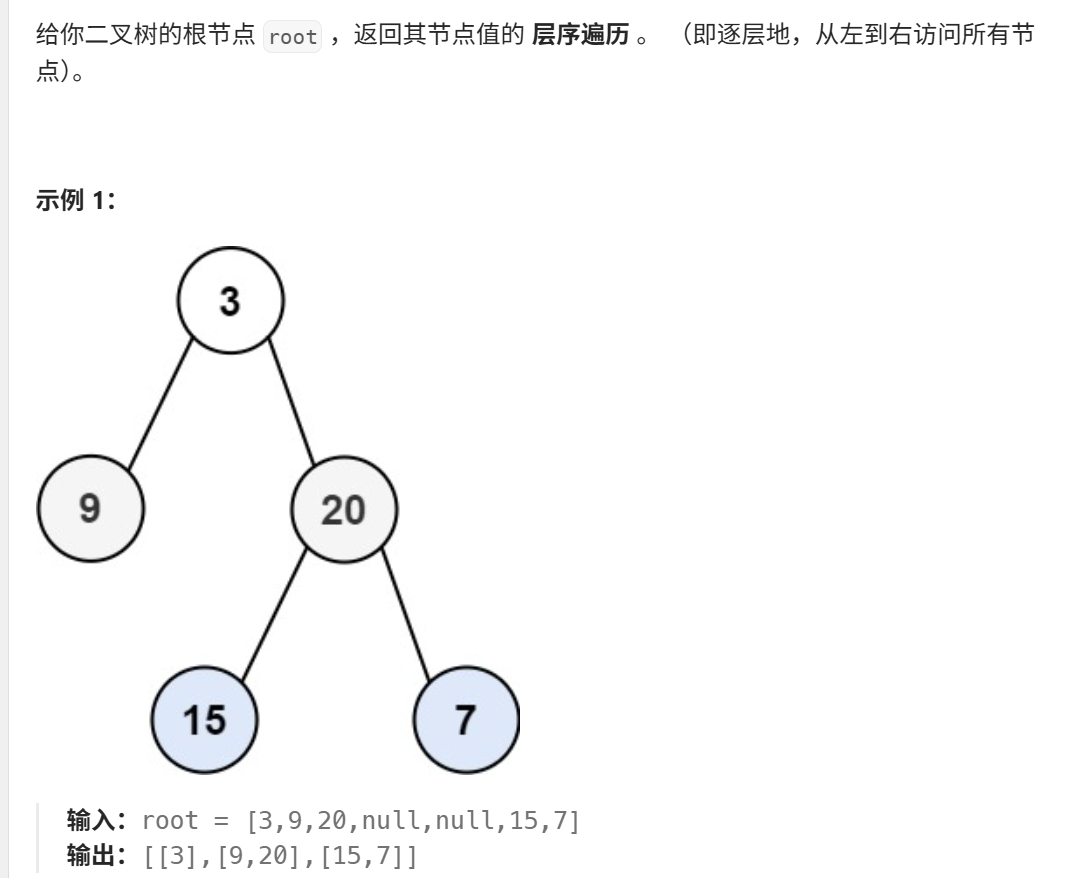
5、 二叉树的层序遍历（力扣102）

java 复制代码 
// 1.利用队列
class Solution {
    public static List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<>();
        if (root == null) {
            return list;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<>();
            // 必须用len暂存长度  
            int len = queue.size();
            /* 遍历当前层，并将当前层所有节点的左右子节点入队列 */
            for (int i = 0; i < len; i++) {
                TreeNode node = queue.poll();
                level.add(node.val);
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
            list.add(level);
        }
        return list;
    }
}

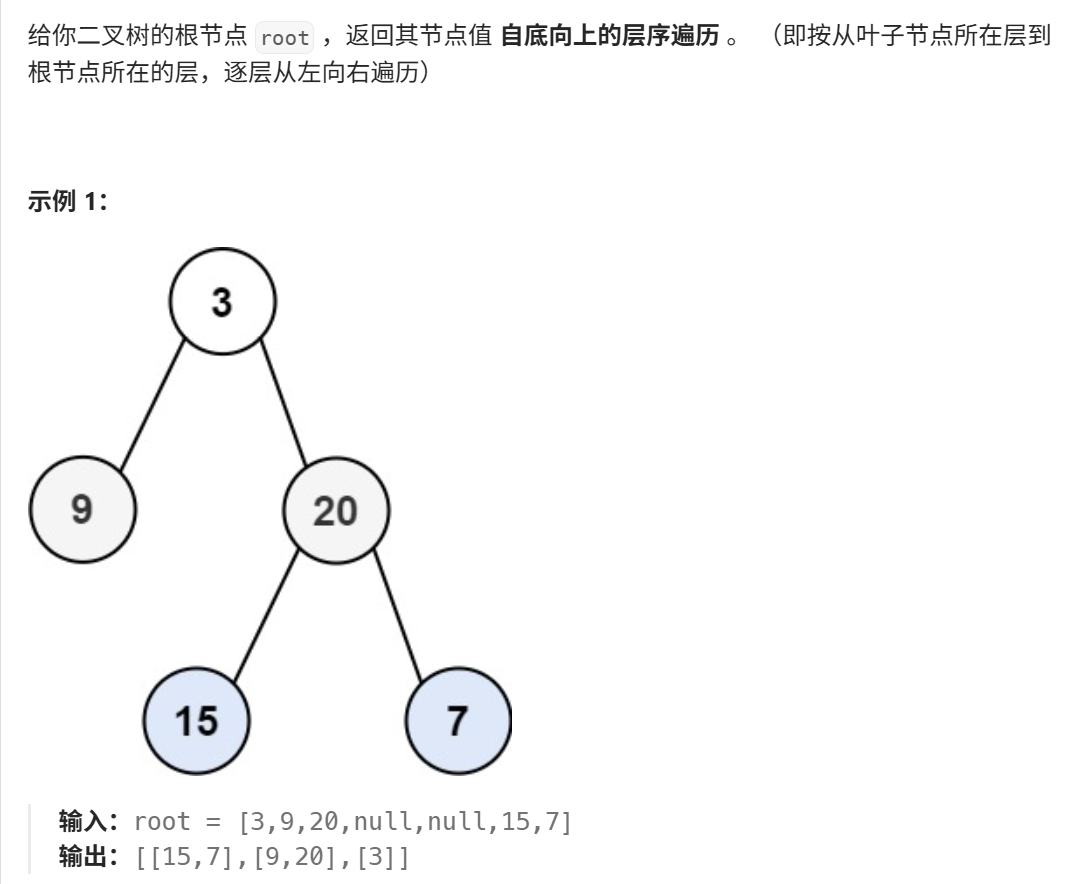
6、二叉树的层序遍历 II（力扣107）

java 复制代码 
//1.层序遍历+栈
    public static List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        Deque<List<Integer>> stack = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> level = new ArrayList<>();
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                TreeNode node = queue.poll();
                level.add(node.val);
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            stack.push(level);
        }

        while(!stack.isEmpty()){
            list.add(stack.pop());
        }
        
        return list;
    }

7、二叉树的右视图（力扣199）

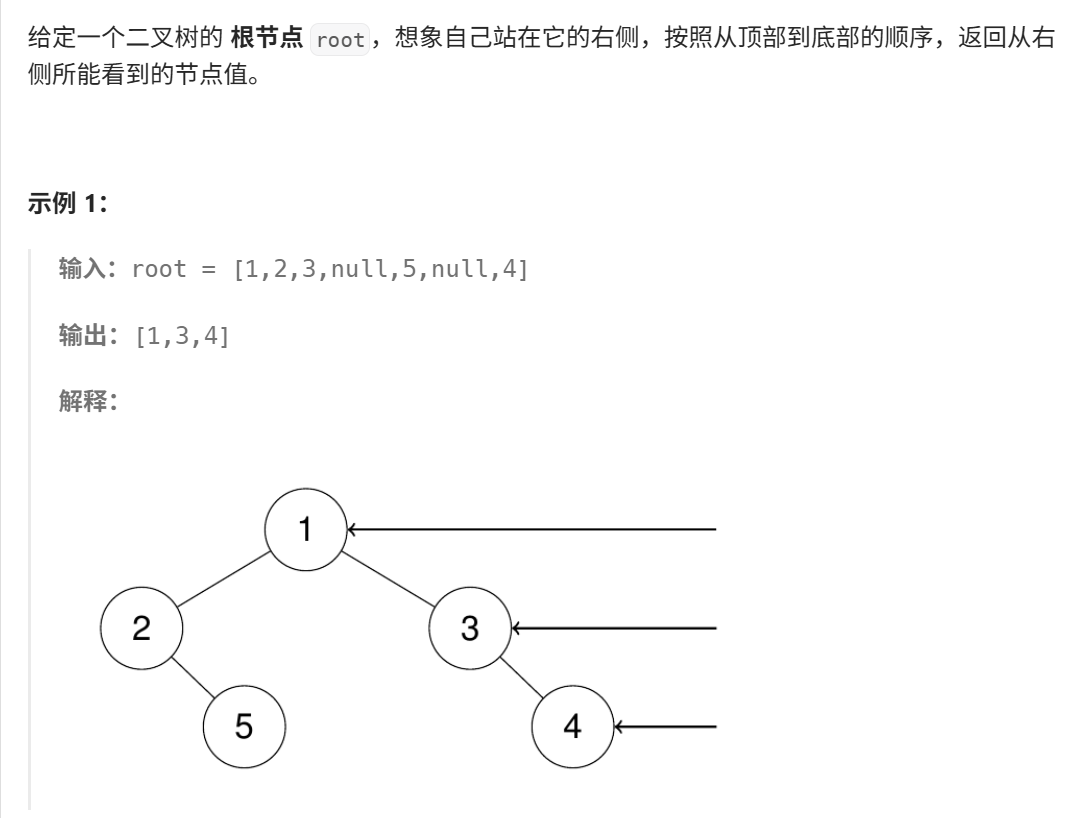
java 复制代码 
//1.利用队列先进先出
    public static List<Integer> rightSideView(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                TreeNode node = queue.poll();
                //只将每一层的最后一个加入到结果集
                if(i == len - 1){
                    list.add(node.val);
                }
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
        }
        return list;
    }

8、二叉树的层平均值（力扣637）

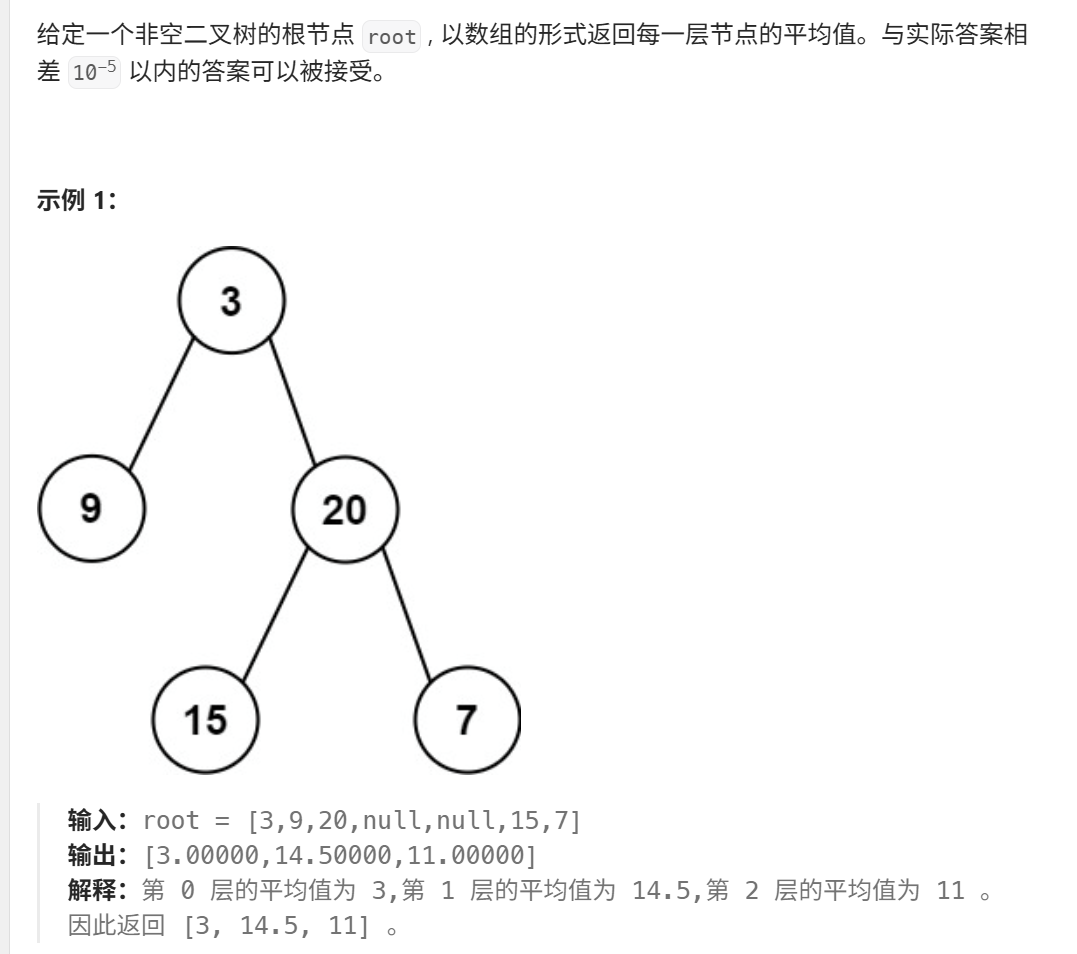
java 复制代码 
//1.利用队列
    public static List<Double> averageOfLevels(TreeNode root) {
        List<Double> list = new ArrayList<>();
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            double sum = 0;
            for(int i = 0;i < len;i++){
                TreeNode node = queue.poll();
                sum += node.val;
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            list.add(sum / len);
        }

        return list;
    }

9、N 叉树的层序遍历（力扣429）

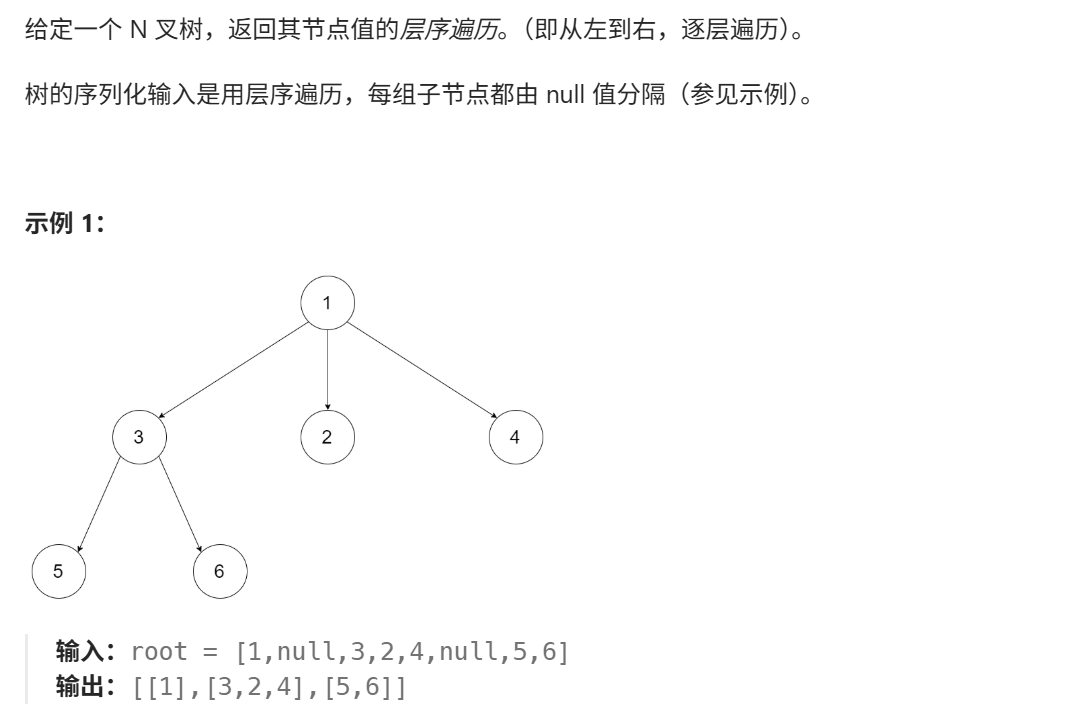
java 复制代码 
//1.利用队列
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> list = new ArrayList<>();
        if(root == null){
            return list;
        }
        
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> level = new ArrayList<>();
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                Node node = queue.poll();
                level.add(node.val);
                if(node.children != null){
                    List<Node> cur = node.children;
                    for(Node n : cur){
                        queue.add(n);
                    }
                }
            }
            list.add(level);
        }
        return list;
    }

10、在每个树行中找最大值（力扣515）

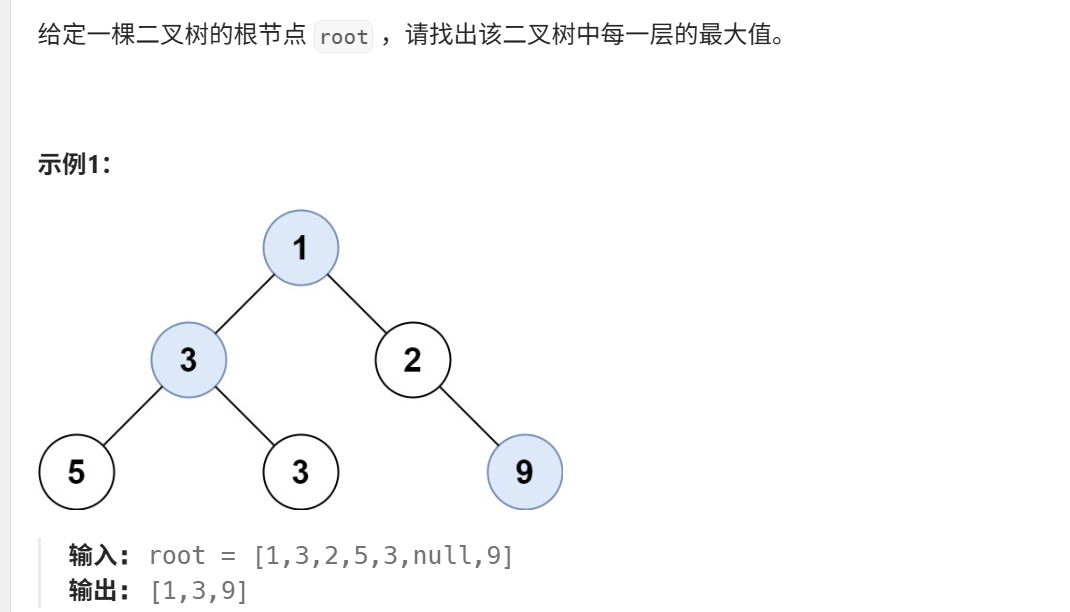
java 复制代码 
//1.利用队列
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            int max = Integer.MIN_VALUE;
            for(int i = 0;i < len;i ++){
                TreeNode node = queue.poll();
                max = Math.max(max,node.val);
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            list.add(max);
        }
        return list;
    }

11、填充每个节点的下一个右侧节点指针（力扣116）

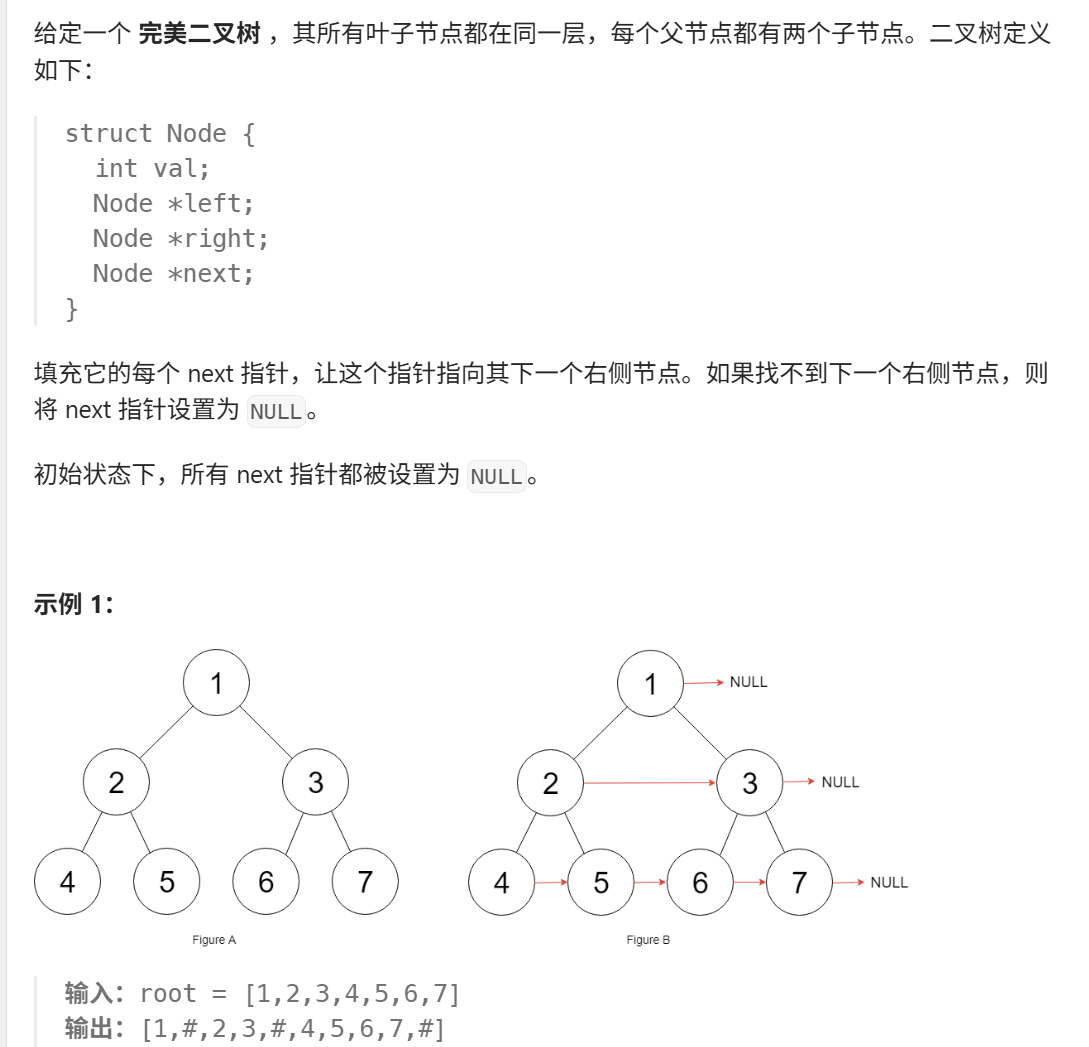
java 复制代码 
//1.队列（非常数空间）
class Solution {
    public static Node connect(Node root) {
        if (root == null) {
            return root;
        }

        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                Node curNode = queue.poll();
                /* 当前层依次串接 */
                if (i < len - 1) {
                    curNode.next = queue.peek();
                }
                if (curNode.left != null) {
                    queue.add(node1.left);
                }
                if (curNode.right != null) {
                    queue.add(node1.right);
                }
            }
        }
        return root;
    }
}
java 复制代码 
//2.常数空间
class Solution {
    public Node connect(Node root) {
        if (null == root){
            return root;
        }
        /* 站在当前树层，将下一层的结点串接起来。此结点用于标识每一层最左边的结点 */
        Node mostLeftNode = root;
        /* 如果有下一层 */
        while (mostLeftNode.left != null){
            Node curNode = mostLeftNode;
            /* 从左到右移动 */
            while (curNode != null){
                curNode.left.next = curNode.right;
                if (curNode.next != null){
                    curNode.right.next = curNode.next.left;
                }
                curNode = curNode.next;
            }
            /* 一层遍历完，从下一层的最左边再开始 */
            mostLeftNode = mostLeftNode.left;
        }
        return root;
    }
}

12、填充每个节点的下一个右侧节点指针 II（力扣117）

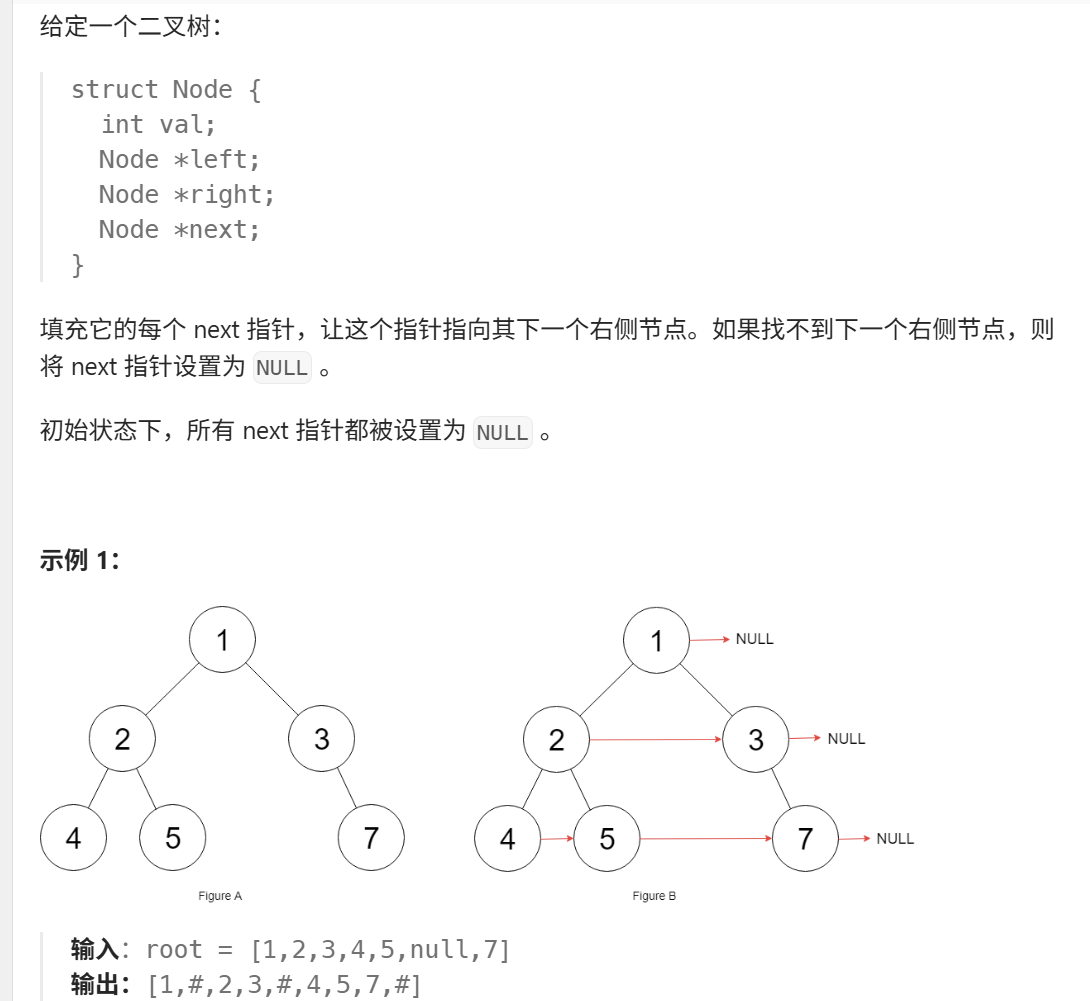
java 复制代码 
//1.队列（非常数空间）
    public Node connect1(Node root) {
        if(root == null){
            return root;
        }

        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                Node node = queue.poll();
                if(i < len - 1){
                    node.next = queue.peek();
                }
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
        }
        return root;
    }
java 复制代码 
// 2.常数空间
class Solution {
    public Node connect(Node root) {
        if (root == null){
            return root;
        }
        Node curNode = root;
        /* 遍历本层，连接下层 */
        while (curNode != null){
            /* 维持每一层最左边的结点，便于切换到下一层 */
            Node mostLeftNode = new Node(0);
            /* 遍历到的结点的前一个结点 */
            Node preNode = mostLeftNode;
            while (curNode != null){
                if (curNode.left != null){
                    preNode.next = curNode.left;
                    preNode = preNode.next;
                }
                if (curNode.right != null){
                    preNode.next = curNode.right;
                    preNode = preNode.next;
                }
                /* 继续向右遍历 */
                curNode = curNode.next;
            }
            /* 切换到下一层 */
            curNode = mostLeftNode.next;
        }
        return root;
    }
}

13、二叉树的最大深度（力扣104）

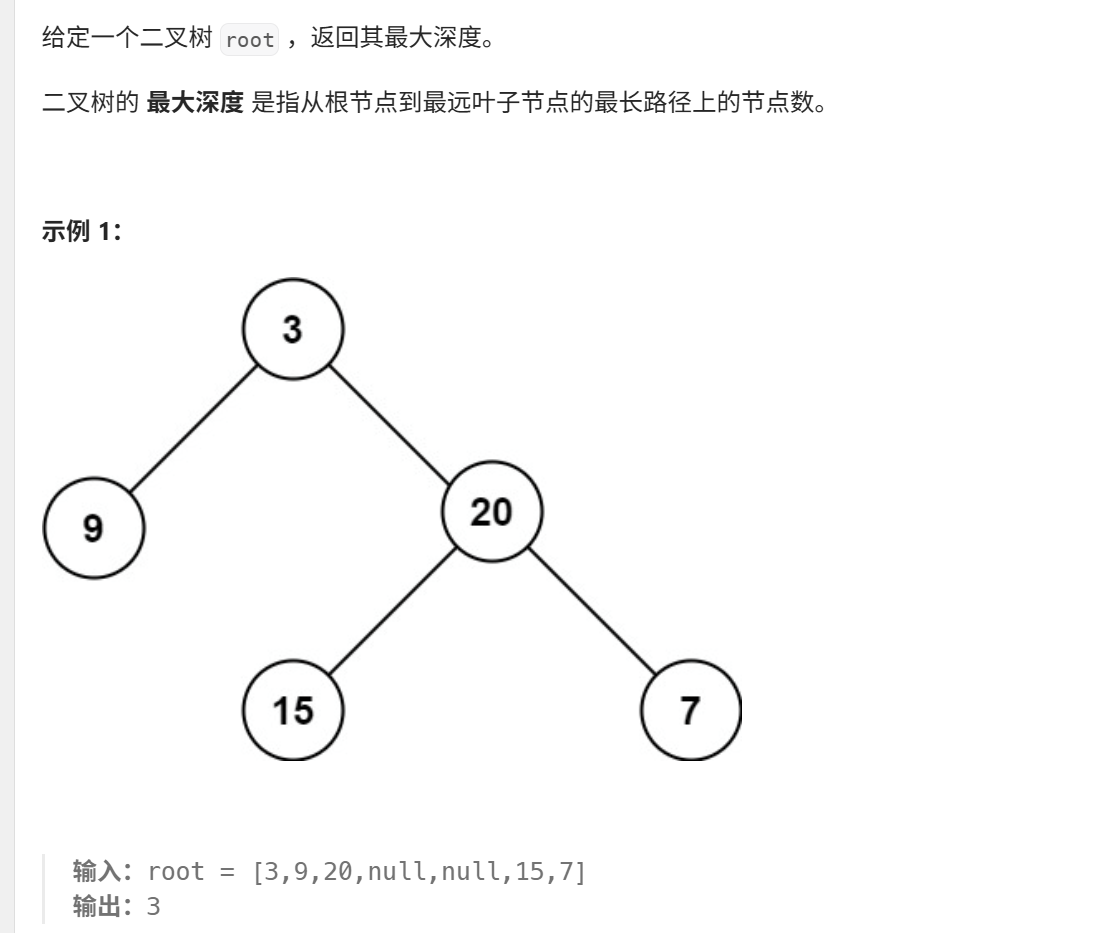
java 复制代码 
//1.递归（传入一个结点，返回以此结点为根结点的最大深度）
    public static int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
java 复制代码 
//2.利用队列，遍历完一层深度加1
    public int maxDepth2(TreeNode root) {
        if(root == null){
            return 0;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int deepth = 0;
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                TreeNode node = queue.poll();
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            deepth ++;
        }
        return deepth;
    }

14、二叉树的最小深度（力扣111）

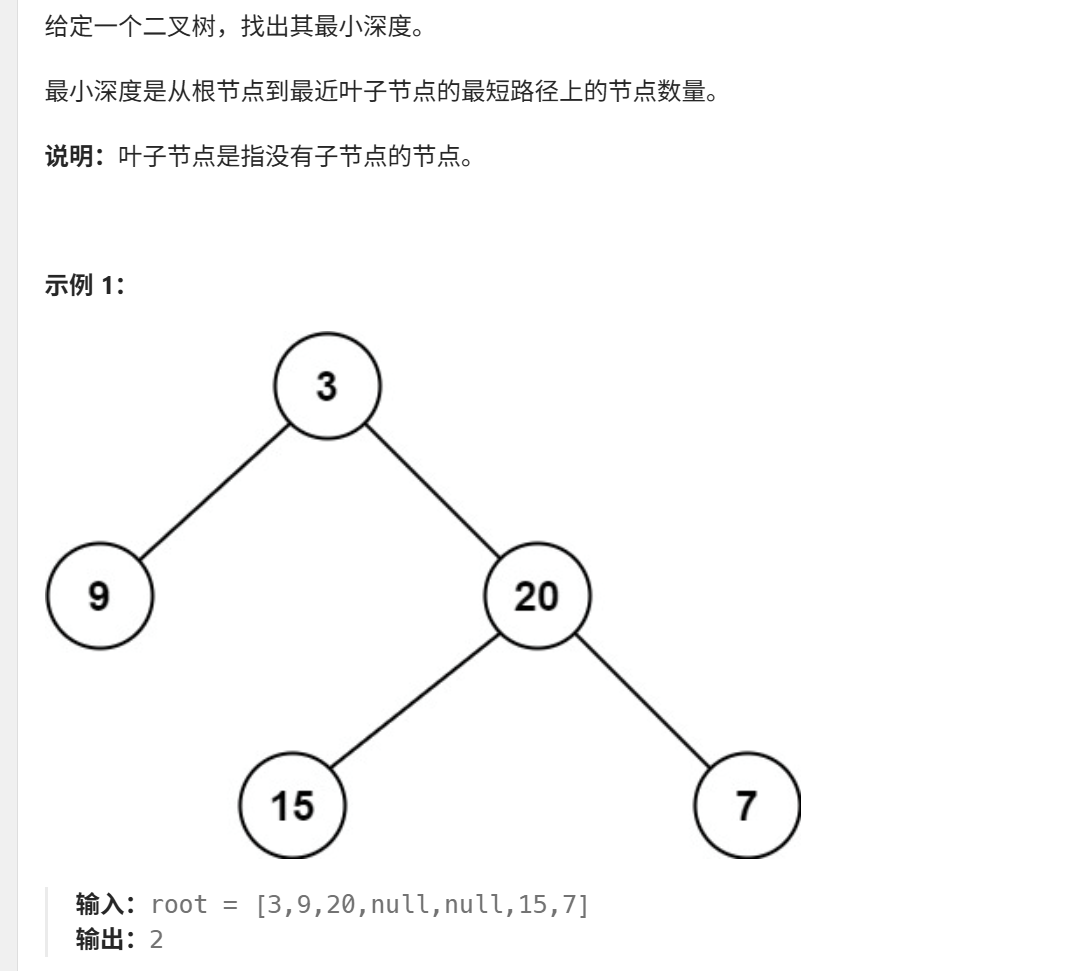
此题注意点：找到离根节点最近的那个"叶子节点"

java 复制代码 
//1.递归
    /*
    * 1.确定递归函数参数和返回值：传入一个节点，返回以此节点为根节点的树的最小深度
    * 2.确定递归的终止条件：当所传入的节点为null，返回为0
    * 3.确定每一层的逻辑：
    *     1.当前节点为null，返回0；
    *     2.当前节点的左子节点和右子节点均为null，返回1；
    *     3.当前节点的左节点或右节点为null，返回 len1 + len2 + 1
    *     4.当前节点的左子节点和右子节点均不为null，返回以两者为根节点的子树的较小值
    * */
    public static int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }

        if(root.left == null && root.right == null){
            return 1;
        }

        int len1 = minDepth(root.left);
        int len2 = minDepth(root.right);
        if(root.left == null || root.right == null){
            return len1 + len2 + 1;
        }

        return Math.min(len1,len2) + 1;
    }
java 复制代码 
//对递归进行简化，情况2和情况4可以合二为一；情况3可以拆分为两个条件
    public static int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }

        if(root.left == null && root.right != null){
            return minDepth(root.right) + 1;
        }
        if(root.right == null && root.left != null){
            return minDepth(root.left) + 1;
        }

        return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
    }
java 复制代码 
//2.队列（层次遍历，比较简单）
    public int minDepth2(TreeNode root) {
        if(root == null){
            return 0;
        }
        
        int depth = 1;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0;i < len;i++){
                TreeNode node = queue.poll();
                //找到了一个叶子节点，直接返回结果
                if(node.left == null && node.right == null){
                    return depth;
                }
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            depth ++;
        }
        return depth;
    }

15、完全二叉树的节点个数（力扣222）

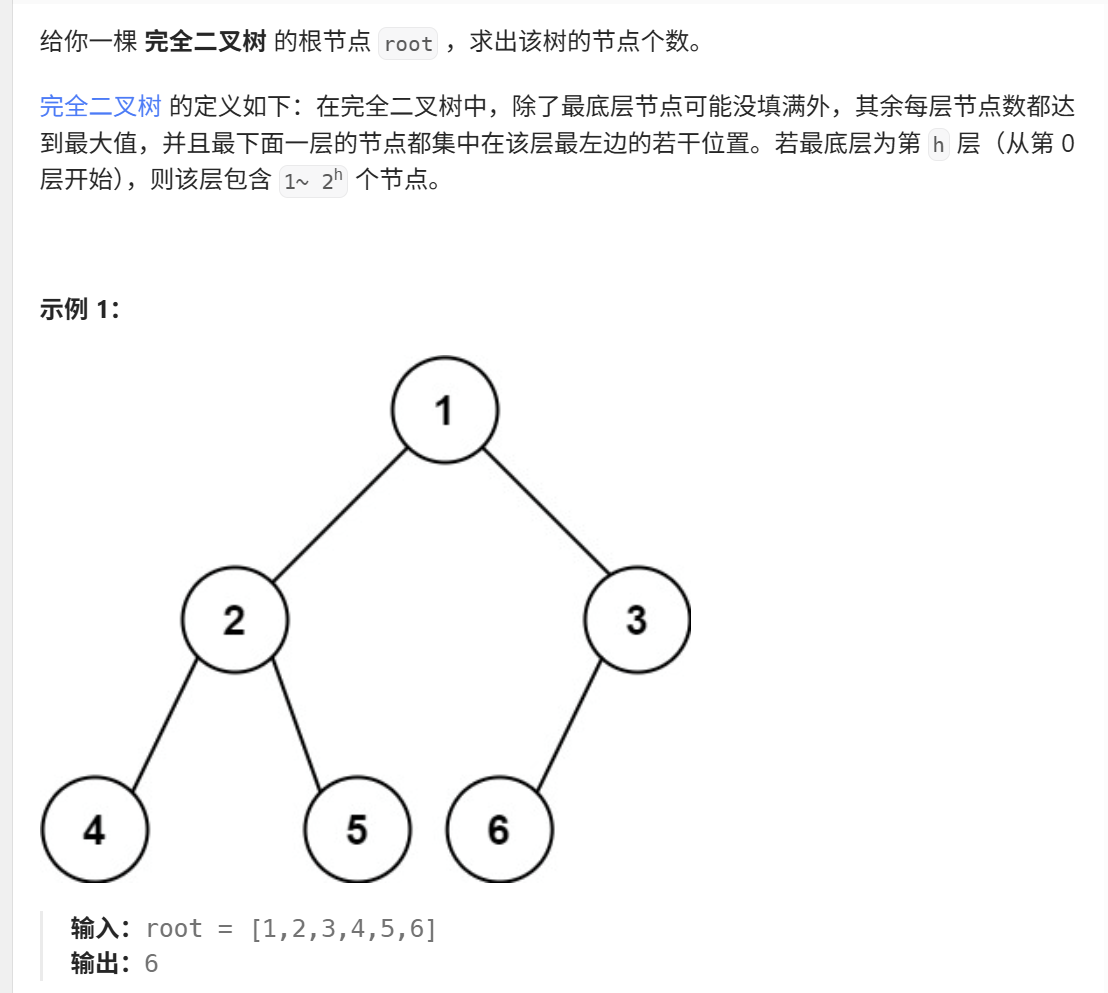
java 复制代码 
//1.递归
    //首先确定递归函数的参数和返回值
    //参数：传入一个节点；返回值：返回以此节点为根节点的树的节点总数量
    public int countNodes(TreeNode root) {
        //如果当前节点为null，直接返回0
        if(root == null){
            return 0;
        }
        //以此节点的左子节点为根节点的树的节点数量
        int leftCount = countNodes(root.left);
        //以此节点的右子节点为根节点的树的节点数量
        int rightCount = countNodes(root.right);
        //返回以此节点为根节点的树的节点数量为 leftCount + rightCount + 此节点的数量1
        return leftCount + rightCount + 1;
    }
java 复制代码 
//2.考虑完全二叉树的特点
    public int countNodes1(TreeNode root) {
        if(root == null){
            return 0;
        }
        //计算以根节点的左子节点为根节点的完全二叉树的高度
        int leftDepth = maxDepth(root.left);
        //计算以根节点的右子节点为根节点的完全二叉树的高度
        int rightDepth = maxDepth(root.right);
        //如果相等，说明以根节点的左子节点为根节点的完全二叉树是满二叉树，总的节点数量为
        //此满二叉树节点数量+根节点数量1+以根节点的右子节点为根节点的完全二叉树的节点数量
        if(leftDepth == rightDepth){
            return (int)Math.pow(2,leftDepth) + count(root.right);
            //如果不相等，说明以根节点的右子节点为根节点的完全二叉树是满二叉树，总的节点数量为
            //此满二叉树节点数量+根节点数量1+以根节点的左子节点为根节点的完全二叉树的节点数量
        }else{
            return (int)Math.pow(2,rightDepth) + count(root.left);
        }
    }

    //计算以此节点为根节点的完全二叉树的节点个数
    public int count(TreeNode root){
        if(root == null){
            return 0;
        }
        return count(root.left) + count(root.right) + 1;
    }

    //计算以此节点为根节点的完全二叉树的高度
    public int maxDepth(TreeNode root){
        if(root == null){
            return 0;
        }
        return maxDepth(root.left) + 1;
    }

16、平衡二叉树（力扣110）

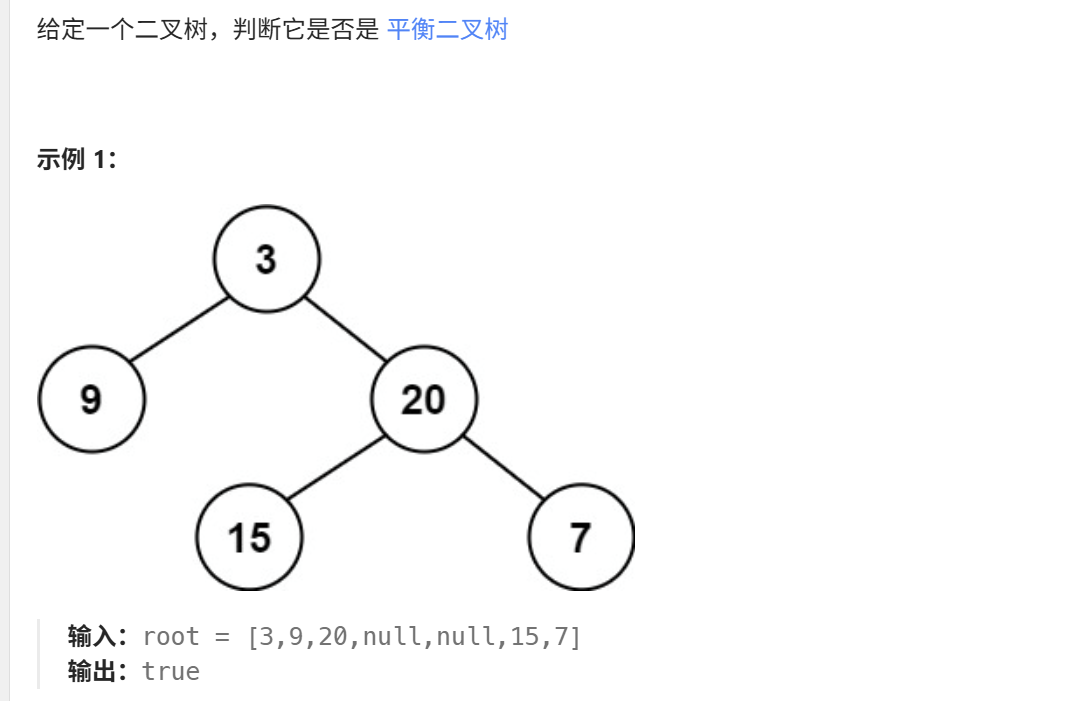
java 复制代码 
//1.二叉树的层次遍历，判断每一个节点的左右子树的高度是否满足要求（自顶向下)
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                TreeNode node = queue.poll();
                if(Math.abs(Depth(node.left) - Depth(node.right)) > 1){
                    return false;
                }
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
        }
        return true;
    }

    //传入一个节点，返回以此节点为根节点的树高度
    public int Depth(TreeNode root){
        if(root == null){
            return 0;
        }
        return Math.max(Depth(root.left), Depth(root.right)) + 1;
    }
java 复制代码 
//2.递归（自顶向下）
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        if(Math.abs(Depth(root.left) - Depth(root.right)) > 1){
            return false;
        }

        return isBalanced(root.left) && isBalanced(root.right);
    }

    //输入一个节点，返回以此节点为根节点的树的高度
    public int Depth(TreeNode root){
        if(root == null){
            return 0;
        }
        return Math.max(Depth(root.left), Depth(root.right)) + 1;
    }
java 复制代码 
//3.递归（自底向上）
    //后续遍历，先看最底下的树是否是平衡二叉树，再层层往上递归
    //时间和空间复杂度都是o(n)
    public boolean isBalanced(TreeNode root) {
        return Depth(root) >= 0;
    }

    public int Depth(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftDepth = Depth(root.left);
        int rightDepth = Depth(root.right);
        if((leftDepth == -1) || (rightDepth == -1) || Math.abs(leftDepth - rightDepth) > 1){
            return -1;
        }else{
            return Math.max(leftDepth, rightDepth) + 1;
        }
    }

17、二叉树的所有路径（力扣257）

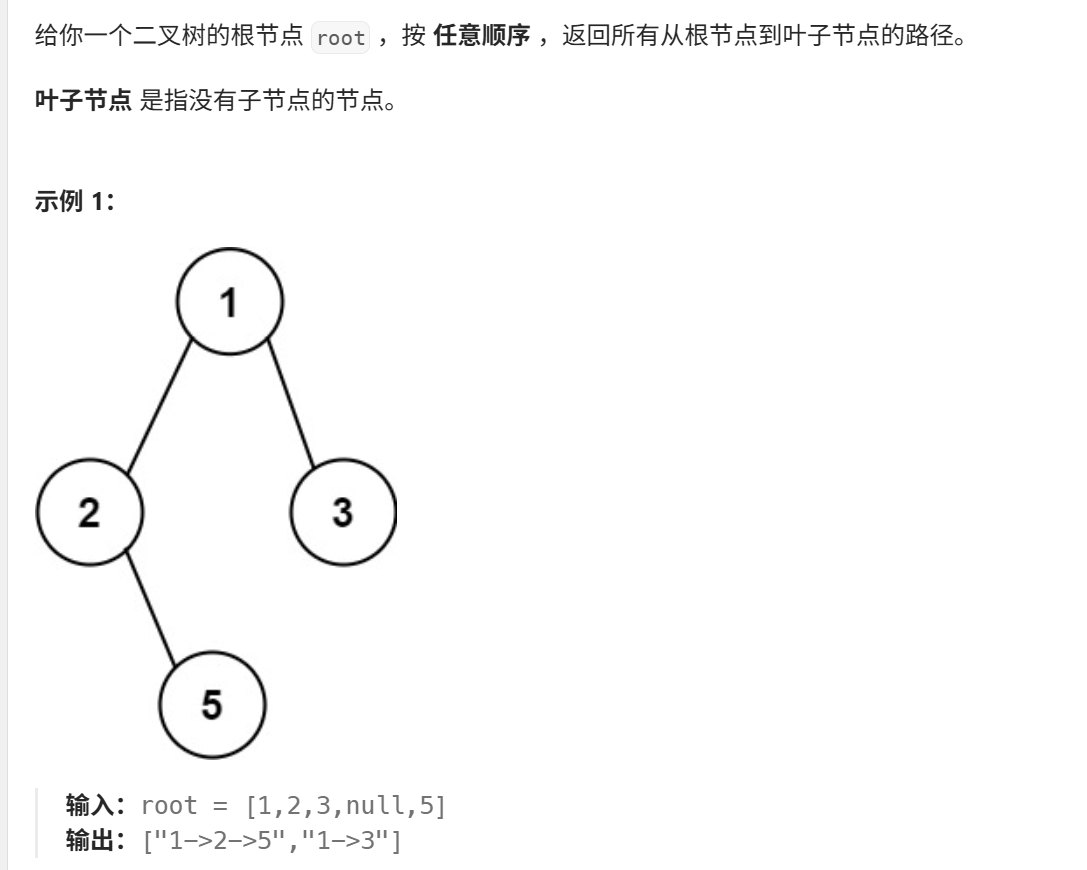
java 复制代码 
//1.回溯(时间和空间复杂度都是O(n2))
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        List<Integer> path = new ArrayList<>();
        travelsal(root, path, res);
        return res;
    }

    //递归+回溯
    //递归函数:每次传入当前节点;path记录从根节点到此节点的路径上的所有节点，便于回溯；
    //res记录最终的结果，每到达一个左右节点均为null的节点，就回溯从根节点到此节点路径
    //上的所有节点，连成一个String，放到res中
    public void travelsal(TreeNode root, List<Integer> path, List<String> res){
        path.add(root.val);
        if(root.left == null && root.right == null){
            int len = path.size();
            StringBuilder sb = new StringBuilder();
            for(int i = 0;i < len - 1;i ++){
                sb.append(path.get(i));
                sb.append("->");
            }
            sb.append(path.get(len - 1));
            res.add(sb.toString());
        }

        if(root.left != null){
            travelsal(root.left, path,res);
            //到这一步，说明上面加入的root.left节点已经用过了，需要及时删除
            path.remove(path.size() - 1);
        }

        if(root.right != null){
            travelsal(root.right, path,res);
            //到这一步，说明上面加入的root.right节点已经用过了，需要及时删除
            path.remove(path.size() - 1);
        }
    }
java 复制代码 
//2.栈（难以想到，不推荐使用）
    public List<String> binaryTreePaths2(TreeNode root) {
        List<String> res = new ArrayList<>();
        if(root == null){
            return res;
        }

        Deque<Object> stack = new LinkedList<>();
        //装入节点
        stack.push(root);
        //装入从根节点到此节点的路径
        stack.push(root.val + "");
        while(!stack.isEmpty()){
            //取出到此节点的路径
            String path = (String)stack.pop();
            //取出此节点
            TreeNode node = (TreeNode)stack.pop();
            //如果当前节点的左右子节点均为null，说明此节点为叶子结点，将路径放入返回集合
            if(node.left == null && node.right == null){
                res.add(path);
            }
            //如果左子节点不为null，将左子节点和到左子节点的路径压栈
            if(node.left != null){
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
            //同样处理右子节点
            if(node.right != null){
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }
        }
        return res;
    }
java 复制代码 
//3.递归（时空复杂度都是O(n2)）
    public List<String> binaryTreePaths3(TreeNode root) {
        List<String> res = new ArrayList<>();
        if(root == null) return res;
        binary(res, new StringBuilder(), root);
        return res;
    }

    public void binary(List<String> res, StringBuilder sb, TreeNode root){
        sb.append(root.val);
        if(root.left == null && root.right == null){
            res.add(sb.toString());
        }
        if(root.left != null){
            //因为每次传进去的都是new的StringBuilder，不用回溯
            binary(res, new StringBuilder(sb).append("->"), root.left);
        }
        if(root.right != null){
            binary(res, new StringBuilder(sb).append("->"), root.right);
        }
    }

18、左叶子之和（力扣404）

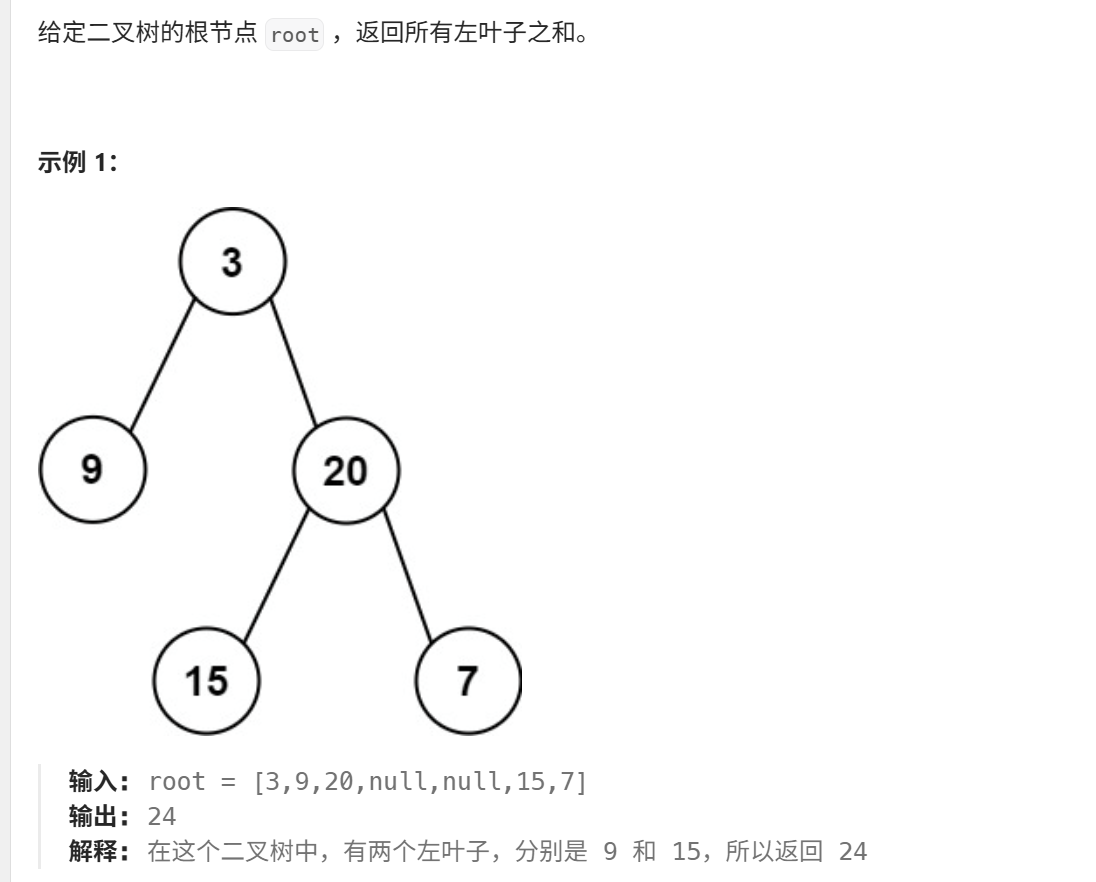
java 复制代码 
//1.层序遍历（当然也可以使用其他的遍历方式，判断每一个节点的左子节点是不是叶子节点）
    public int sumOfLeftLeaves(TreeNode root) {
        int sum = 0;
        if(root == null){
            return sum;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0;i < len;i ++){
                TreeNode node = queue.poll();
                //站在当前层看下一层：
                //如果当前节点的左子节点不为空，并且当前节点的左子节点的左子节点和右子节点均为空，则此节点的左子节点为左叶子节点
                if(node.left != null && node.left.left == null && node.left.right == null){
                    sum += node.left.val;
                }

                if(node.left != null){
                    queue.add(node.left);
                }

                if(node.right != null){
                    queue.add(node.right);
                }
            }
        }
        return sum;
    }
java 复制代码 
//2.递归
    //递归函数：每次传入一个节点，返回以此节点为根节点的树的左叶子节点的和
    //自底向上，使用后序遍历
    public int sumOfLeftLeaves2(TreeNode root) {
        if(root == null){
            return 0;
        }
				
		// 左
        int leftValue = sumOfLeftLeaves(root.left);
        // 右
        int rightValue = sumOfLeftLeaves(root.right);
		// 当前结点
        int midValue = 0;
        if(root.left != null && root.left.left == null && root.left.right == null){
            midValue = root.left.val;
        }
        return leftValue + rightValue + midValue;
    }

19、找树左下角的值（力扣513）

java 复制代码 
//1.层序遍历，每遍历到每层的第一个节点时，将返回值替换为此节点值
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int res = root.val;
        boolean flag = true;
        while(!queue.isEmpty()){
            int len = queue.size();
            for(int i = 0; i < len; i ++){
                TreeNode node = queue.poll();
                // 遍历到每一层的第一个结点时flag=true
                if(flag){
                    res = node.val;
                    flag = false;
                }
                if(node.left != null){
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            flag = true;
        }
        return res;
    }
java 复制代码 
//2.递归，采用前序遍历
    //用来记录最大深度
    private int Deep = -1;
    //返回值
    private int value = 0;

    public int findBottomLeftValue2(TreeNode root) {
        value = root.val;
        findLeftValue(root, 0);
        return value;
    }

    //递归函数
    //传入节点和当前节点的深度
    //采用前序遍历，保证每次到达最大深度所取得值是最左边的
    private void findLeftValue(TreeNode root, int deep){
        if(root == null){
            return;
        }
        if(root.left == null && root.right == null){
            //保证每次到达一个更大深度时，所取的值是最左边的
            if(deep > Deep){
                value = root.val;
                // 更新最大深度
                Deep = deep;
            }
        }
        findLeftValue(root.left, deep + 1);
        findLeftValue(root.right, deep + 1);
    }

20、路径总和（力扣112）

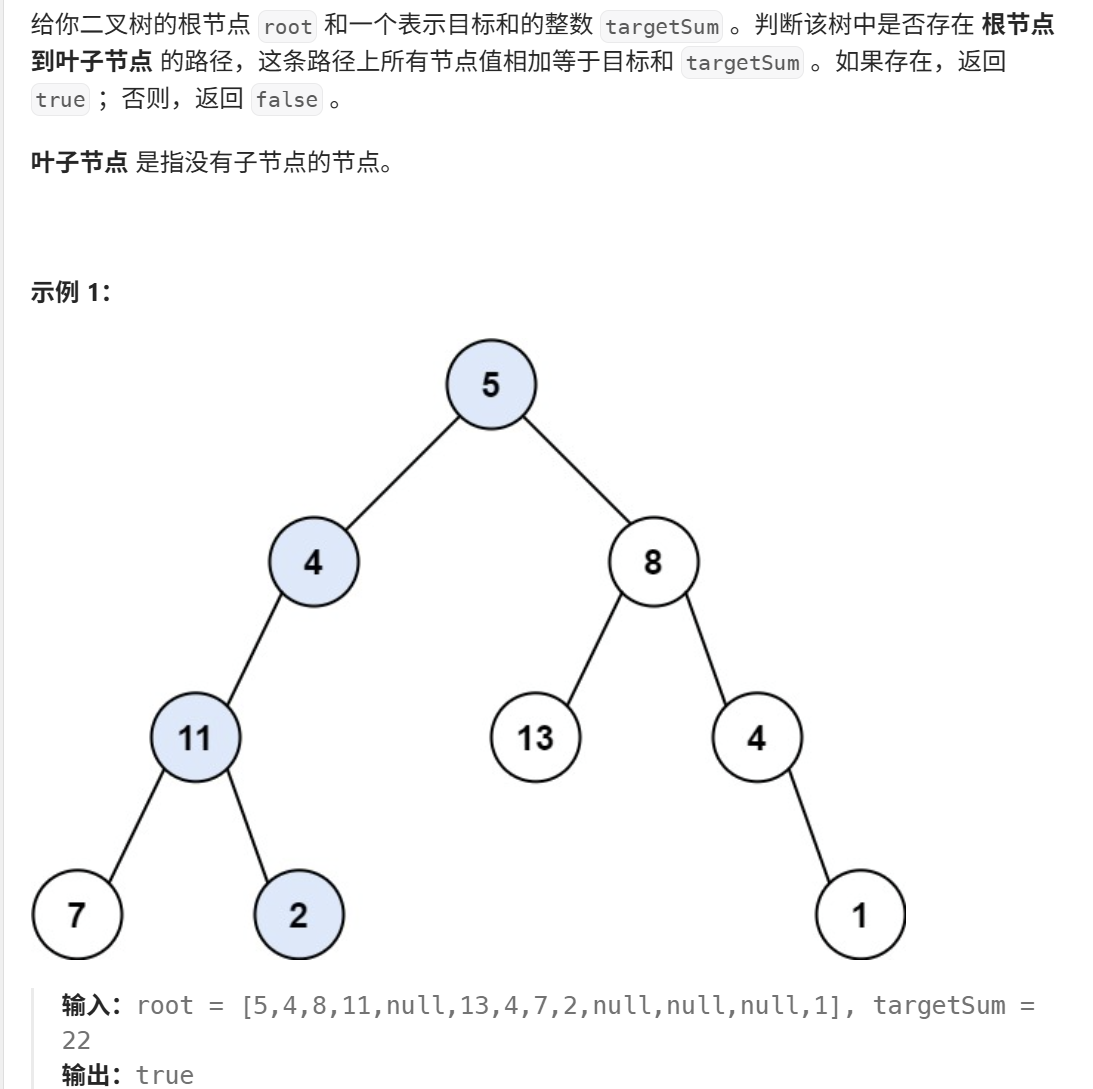
java 复制代码 
//1.递归，每次传入递归函数的是相减的值，代码比较简洁
    public boolean hasPathSum2(TreeNode root, int targetSum) {
        if(root == null){
            return false;
        }
        // 当前结点为叶子结点且路径和符合要求
        if(root.left == null && root.right == null && targetSum - root.val == 0){
            return true;
        }
        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }
java 复制代码 
//2.层序遍历，利用两个队列，分别存放节点和到此节点路径上的节点的和
    public boolean hasPathSum3(TreeNode root, int targetSum) {
        if(root == null){
            return false;
        }
        Queue<TreeNode> queueNode = new LinkedList<>();
        Queue<Integer> queueInt = new LinkedList<>();
        queueNode.add(root);
        queueInt.add(root.val);
        while(!queueNode.isEmpty()){
            int len = queueNode.size();
            for(int i = 0; i < len; i ++){
                TreeNode node = queueNode.poll();
                int value = queueInt.poll();
                if(node.left == null && node.right == null && value == targetSum){
                    return true;
                }
                if(node.left != null){
                    queueNode.add(node.left);
                    queueInt.add(node.left.val + value);
                }
                if(node.right != null){
                    queueNode.add(node.right);
                    queueInt.add(node.right.val + value);
                }
            }
        }
        return false;
    }
相关推荐
老鼠只爱大米2 小时前
LeetCode经典算法面试题 #199：二叉树的右视图（BFS双队列法、DFS递归法等多种实现方案详细解析）
算法·leetcode·二叉树·dfs·bfs·深度优先搜索·右视图
历程里程碑2 小时前
子串-----和为 K 的子数组
java·数据结构·c++·python·算法·leetcode·tornado
We་ct2 小时前
LeetCode 383. 赎金信：解题思路+代码解析+优化实战
前端·算法·leetcode·typescript
皮皮哎哟3 小时前
数据结构：从队列到二叉树基础解析
c语言·数据结构·算法·二叉树·队列
一匹电信狗3 小时前
【高阶数据结构】并查集
c语言·数据结构·c++·算法·leetcode·排序算法·visual studio
WBluuue3 小时前
数据机构与算法：dp优化——倍增优化
c++·算法·leetcode·动态规划
圣保罗的大教堂4 小时前
leetcode 3013. 将数组分成最小总代价的子数组 II 困难
leetcode
划破黑暗的第一缕曙光4 小时前
[数据结构]：6.二叉树链式结构的实现2
c语言·数据结构·二叉树
iAkuya5 小时前
(leetcode)力扣100 59括号生成（回溯||按括号序列的长度递归）
算法·leetcode·职场和发展
热门推荐
01GitHub 镜像站点02Clawdbot 中文汉化版 接入微信、飞书03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services05OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书06Claude Code Skills 实用使用手册07UV安装并设置国内源08Linux下V2Ray安装配置指南09在Trae中使用Pencil MCP102026美赛A题智能手机电池续航时间预测的连续时间数学模型