一、结构风荷载理论概述
结构风荷载是风对建筑物、桥梁、大跨结构等的作用力,其理论发展经历了从静力风荷载 到动力风荷载 的演变,核心是随机振动理论 与流体动力学的结合。
1. 风荷载的组成
风荷载可分为平均风荷载 (稳定风,由风的长周期成分引起)和脉动风荷载(阵风,由风的短周期湍流引起)。平均风荷载是静力荷载,脉动风荷载是动力荷载,需考虑其对结构的动力响应(如振动、位移、内力)。
2. 风荷载的计算方法
-
静力风荷载 :采用风荷载体型系数 (μsμ_sμs)和基本风压 (w0w_0w0),公式为:
wk=βzμsμzw0w_k=β_zμ_sμ_zw_0wk=βzμsμzw0
其中,βzβ_zβz为风振系数(考虑动力放大效应),μzμ_zμz为风压高度变化系数。
-
动力风荷载 :需模拟脉动风速时程 (如AR模型、谐波叠加法),结合风致响应分析(如虚拟激励法、时程分析法),计算结构的位移、速度和加速度响应。
3. 关键理论模型
-
Davenport风速谱:描述脉动风速的功率谱密度,是风工程中最常用的谱模型之一,公式为:
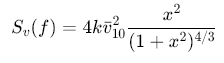
其中,kkk为地面粗糙度系数,vˉ10vˉ10vˉ10为10米高度处的平均风速,x=1200f/vˉ10x=1200f/vˉ10x=1200f/vˉ10(f为频率)。
AR模型(自回归模型):用于模拟脉动风速时程,通过线性滤波法生成具有时空相关性的风速序列,公式为:
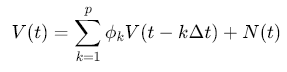
其中,ϕkϕ_kϕk为回归系数,N(t)N(t)N(t)为白噪声。
二、Matlab在结构风荷载计算中的应用
Matlab是结构风荷载计算的重要工具,可实现风荷载模拟 、风致响应分析 和等效静力风荷载计算,以下是具体应用场景及代码示例。
1. 脉动风速时程模拟(AR模型)
目标:生成具有时空相关性的脉动风速时程,用于风致响应分析。
步骤:
- 确定Davenport风速谱参数(如k=0.00464(C类场地)、vˉ10=26.8m/s);
- 计算协方差矩阵(通过Wiener-Khinchin定理,由功率谱密度得到);
- 求解AR模型回归系数(通过Yule-Walker方程);
- 生成白噪声序列,代入AR模型生成风速时程。
代码示例(参考):
matlab
% 参数设置
N = 1024; % 采样点数
dt = 0.1; % 时间步长(s)
f_cutoff = 10; % 截断频率(Hz)
k = 0.00464; % 地面粗糙度系数(C类场地)
v10 = 26.8; % 10米高度平均风速(m/s)
% 生成频率数组
f = (0:N/2-1)/(N*dt); % 频率范围(Hz)
x = 1200*f/v10; % Davenport谱参数
% 计算Davenport风速谱
S_v = 4*k*v10^2 * x.^2 ./ (1+x.^2).^(4/3);
% 生成协方差矩阵(简化,实际需通过FFT计算)
R = ifft(S_v); % 协方差函数(维纳-辛钦定理)
% 求解AR模型回归系数(Yule-Walker方程)
p = 10; % AR模型阶数
phi = aryule(R, p); % 回归系数
% 生成白噪声序列
N_t = randn(N, 1); % 高斯白噪声
% 生成脉动风速时程(AR模型)
V = filter(phi, 1, N_t); % 线性滤波
% 绘制风速时程
figure;
plot((0:N-1)*dt, V);
xlabel('时间(s)');
ylabel('脉动风速(m/s)');
title('AR模型模拟的脉动风速时程');
grid on;2. 风致响应分析(虚拟激励法)
目标:计算大跨结构(如网壳、挑篷)在脉动风作用下的位移响应。
步骤:
- 建立结构动力模型(质量矩阵M、刚度矩阵K、阻尼矩阵C);
- 生成虚拟激励(由脉动风速谱得到);
- 计算结构响应(通过虚拟激励法,直接求解位移均方根)。
代码示例(参考):
matlab
% 结构参数(简化为2自由度系统)
m1 = 1000; m2 = 500; % 质量(kg)
k1 = 2e5; k2 = 1e5; % 刚度(N/m)
c1 = 2e3; c2 = 1e3; % 阻尼(N·s/m)
M = [m1, 0; 0, m2]; % 质量矩阵
K = [k1+k2, -k2; -k2, k2]; % 刚度矩阵
C = [c1+c2, -c2; -c2, c2]; % 阻尼矩阵
% 虚拟激励(由Davenport谱生成)
f = (0:100)/100; % 频率范围(Hz)
S_v = 4 * 0.00464 * 26.8^2 * (1200*f/26.8).^2 ./ (1+(1200*f/26.8).^2).^(4/3); % Davenport谱
excitation = sqrt(S_v); % 虚拟激励幅值
% 计算结构响应(虚拟激励法)
omega = 2*pi*f; % 角频率(rad/s)
H = inv(-omega.^2*M + 1i*omega*C + K); % 传递函数
response = H * excitation; % 响应(复数)
% 绘制位移响应谱
figure;
plot(f, abs(response));
xlabel('频率(Hz)');
ylabel('位移响应(m)');
title('虚拟激励法计算的位移响应谱');
grid on;3. 等效静力风荷载计算(三分量法)
目标:将动力风荷载转化为等效静力荷载,用于结构设计。
步骤:
- 分解风致响应 为平均分量 (平均风引起)、背景分量 (脉动风的低频成分)、共振分量(脉动风的高频成分与结构共振);
- 计算等效静力风荷载(由各分量组合而成)。
代码示例(参考):
matlab
% 响应分量(假设已通过风致响应分析得到)
mean_response = 0.1; % 平均位移(m)
background_response = 0.05; % 背景位移(m)
resonance_response = 0.03; % 共振位移(m)
% 组合响应(三分量法)
total_response = mean_response + background_response + resonance_response;
% 计算等效静力风荷载(假设结构刚度k=1e5 N/m)
k = 1e5; % 结构刚度(N/m)
equivalent_load = k * total_response; % 等效静力荷载(N)
% 输出结果
fprintf('等效静力风荷载:%.2f N\n', equivalent_load);参考代码 结构风荷载理论与Matlab计算 www.youwenfan.com/contentcsq/80130.html
三、工程应用案例
以大跨体育场挑篷结构为例,说明Matlab在风荷载计算中的应用:
- 问题:挑篷结构质量轻、柔度大,风致振动显著,需计算其风振响应。
- 方法 :采用AR模型 模拟脉动风速时程,结合时程分析法计算结构的位移响应。
- 结果:模拟的风速谱与目标谱(Davenport谱)吻合良好,结构的位移响应最大值为0.02m,满足设计要求。
四、注意事项
- 参数选择:地面粗糙度系数k、平均风速vˉ10等参数需根据场地条件(如C类场地k=0.00464)合理选择。
- 模型阶数:AR模型的阶数p需通过**赤池信息准则(AIC)**确定,避免过拟合或欠拟合。
- 验证 :模拟结果需与风洞试验 或规范(如《建筑结构荷载规范》GB50009-2012)对比,确保准确性。
五、总结
结构风荷载理论是随机振动 与流体动力学 的交叉学科,Matlab是实现风荷载计算的重要工具,可用于脉动风速模拟 、风致响应分析 和等效静力风荷载计算。