进阶篇-8-数学篇-7--特征值与特征向量：AI特征提取的核心逻辑

特征值与特征向量：AI 特征提取的核心逻辑

作者：Weisian
日期：2026年1月28日

在前几篇文章中，我们一步步揭开了向量、矩阵、张量的神秘面纱------它们是 AI 用来描述世界、承载数据的"数字语言"。

向量是串起多个特征的"线条"；
矩阵是铺展平面信息的"表格"；
张量是装下高维复杂场景的"集装箱"。

你有没有想过一个问题：

当 AI 拿到一张 224×224 的彩色图片（4D 张量），里面有上百万个像素值，它该如何快速抓住"这是一只猫"的核心信息，而不是被杂乱的像素噪音干扰？
当推荐系统拿到用户的几十项行为数据（向量），它该如何筛选出"决定用户喜好"的关键特征，而不是在无关数据中浪费算力？

答案藏在一对相辅相成的数学概念里------特征值（Eigenvalue）与特征向量（Eigenvector）。

如果说向量、矩阵、张量是 AI "储存信息"的容器，

那么特征值与特征向量，就是 AI "提炼核心信息"的"黄金筛子"。

它们是线性代数的核心，更是 AI 特征提取、数据降维、模式识别的"幕后功臣"------从图片压缩、人脸识别，到 PCA 降维、谱聚类，再到深度学习中的权重矩阵分析，都离不开它们的身影。

今天，我们就从"矩阵变换的不变方向"这个核心视角，由浅入深揭开特征值与特征向量的神秘面纱，用形象的比喻、手动推导和代码实操，看懂它们如何成为 AI 从海量数据中"抓重点"的核心逻辑。

一、从直觉到数学：什么是"特征"？

我们先抛开所有公式，从最贴近生活的感知出发，一步步看清"特征"到底是什么。

不妨先做一个简单的观察：收集100个人的身高、体重数据，把每一个人都记作一组[身高，体重]的二维数据，将这些数据点画在坐标系里，你会立刻发现一个规律------

这些点并不会杂乱无章地散落，而是紧紧贴着一条倾斜的直线分布：身高越高的人，体重往往也越重，二者呈现出清晰的正向关联。

原始的坐标轴，是独立的"身高轴"和"体重轴"，它们只是两个孤立的衡量维度；而这条斜着的、贯穿大部分数据的趋势线，才是藏在数据背后、更能代表整体规律的核心方向 。

它浓缩了两组数据的关联，比单一的身高或体重，更能概括这100个人的身体特征规律。

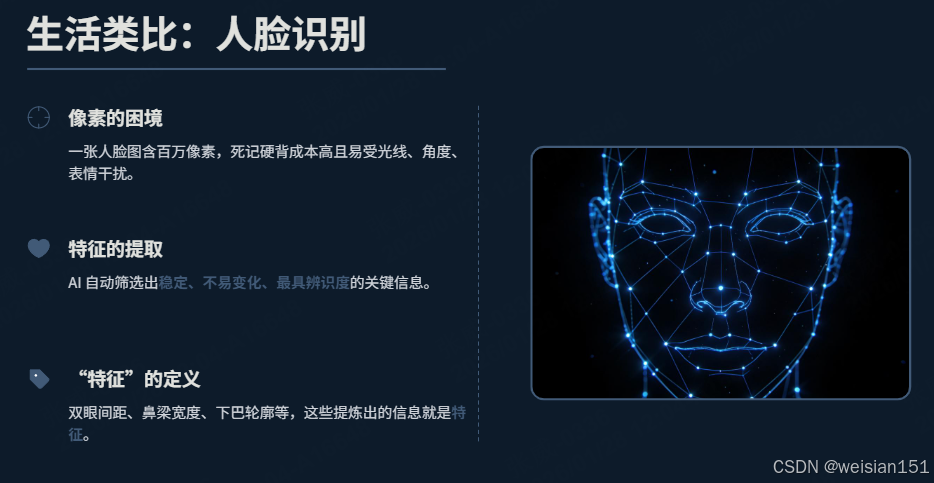
生活类比：人脸识别的"关键特征"

再换一个场景，我们每天都在接触的人脸识别，背后同样是"找特征"的逻辑。

一张普通的人脸图片，可能包含几十万甚至上百万个像素点，每个像素只有单一的颜色数值，既零散又冗余。如果让AI死记每一个像素，不仅计算成本极高，还极易受到光线、角度、表情的干扰，稍微换个环境就无法识别。

所以AI不会这么做。

它会自动筛选出那些稳定、不易变化、最具辨识度 的关键信息：比如双眼的间距、鼻梁的宽度与高度、下巴的轮廓弧度、眉骨的走向......这些经过提炼的信息，就是我们所说的特征。

它们舍弃了无关的像素噪音，只保留最能区分"这张脸和其他脸"的核心信息，让识别变得高效、准确。

💡 这就是特征提取的核心思想 ：
从海量、冗余、杂乱的原始信息里，找到少数几个最具代表性的"核心方向"，用最精简的方式，完整描述整个数据集的本质规律。

而在严谨的数学体系中，能够精准实现这一思想，帮我们从数据中"抓重点、找规律"的核心工具，正是接下来要深入讲解的------特征值与特征向量。

二、核心前提：矩阵 = 一种"数据变换"

在理解特征值与特征向量之前，我们必须先刷新对"矩阵"的认知------它不只是一张静态的数字表格，更本质的是，一个矩阵对应着一种特定的线性变换。

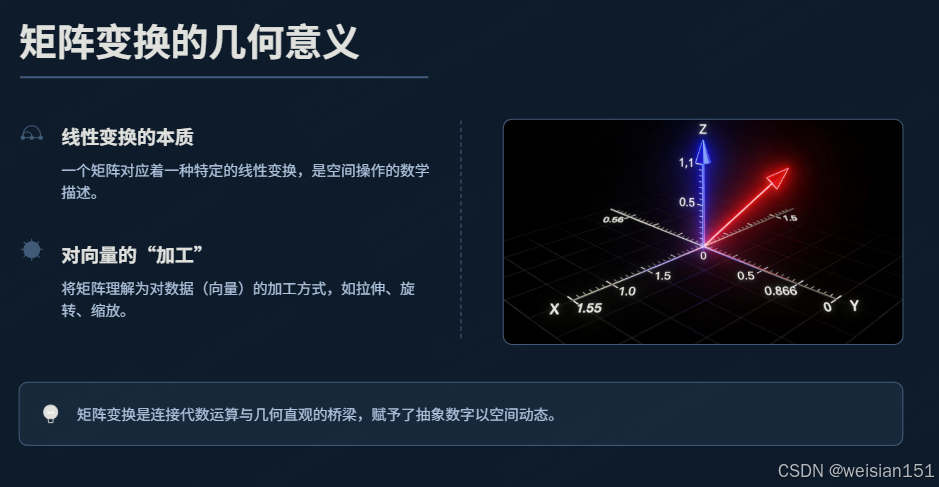
就像我们之前聊到的，快递分拣的矩阵是"分拣规则"，美颜滤镜的矩阵是"磨皮规则"，而这里的"矩阵变换"，可以理解为对一组数据（向量）的"加工方式"------比如拉伸、旋转、缩放。

2.1 生活类比：矩阵 = 一台"数据加工机器"

想象你有一堆塑料棒（向量），现在你有一台机器（矩阵），把塑料棒放进去，机器会对它做两种操作之一：

既拉伸/压缩，又旋转：比如把一根竖直的塑料棒，变成一根倾斜的、更长的塑料棒；
只拉伸/压缩，不旋转：比如把一根竖直的塑料棒，变成一根更长（或更短）的竖直塑料棒，方向完全不变。

而这第二种情况，就是我们要找的"特征场景"------那些经过矩阵变换后，方向保持不变，只发生伸缩变化的向量，就是这个矩阵的特征向量；而伸缩的比例，就是对应的特征值。

补充：通俗理解"方向不变性"的核心意义

很多人学到这里都会卡住：明明只是数学上"方向不变"的性质，为什么就能成为AI提取有效信息的关键？

我们先把抽象概念彻底落地，再一层层讲透它和图像识别、抗干扰、降噪的真实关联。

（1）、什么是"方向不变性"？

先明确核心定义：

"方向不变"不是向量完全静止不动 ，而是向量在经过矩阵变换后，仍然落在原来所在的直线上，只发生长度的拉伸或压缩，完全不发生角度的偏转、旋转或偏移 。

满足这个条件的向量，就是这个矩阵的特征向量 ；拉伸或压缩的倍数，就是对应的特征值。

我们举两个更直观、更贴近"变换"场景的例子：

例子1：舞台上的追光灯

想象舞台中央有一盏固定安装的追光灯，灯头只能沿着竖直方向上下摆动，不能左右转动。

无论你把灯头调得更亮、投射范围拉得更大（对应拉伸），还是调暗、收窄范围（对应压缩），它始终只能照亮竖直方向的一条直线 ，灯光的主轴方向永远不会偏到左侧或右侧。

这个"竖直不变的光照主轴"，就对应数学上的特征向量方向 ；灯光范围缩放的程度，就是特征值 。

如果这盏灯可以随意左右旋转，照亮不同方向，那就不再是"特征方向"，而是普通的向量变换。
例子2：可伸缩的旗杆

一根垂直固定在地面的旗杆，本身可以通过伸缩结构改变高度。

你把旗杆拉长、或是缩短收回，它始终保持垂直于地面 ，不会歪向任何一侧，也不会发生任何角度的倾斜。

这种"只改变长短、不改变朝向"的特性，就是特征向量的方向不变性 。

反之，如果你把旗杆强行掰弯、推倒，让它指向斜方，就同时发生了旋转和形变，不再符合特征向量的定义。

简单总结：
方向不变，就是向量经过矩阵变换后，仍在原来的直线上，仅做长度的伸缩，没有任何角度的偏转。

（2）、方向不变，为什么就等于"有用信息"？

这是整个章节最容易困惑的地方，我们用图像识别的真实逻辑，把"方向不变"和"有效特征"直接绑定。

我们可以先建立一个核心认知：

在现实数据里，稳定不变的规律，才是有用信息；容易随环境乱动、随机变化的，大多是噪音。

把这个认知对应到矩阵变换和特征向量上，逻辑就完全通顺了：

把"图像变化"看作一次矩阵变换
在图像处理中，我们可以把光照变化、噪声叠加、轻微角度偏移等影响，整体抽象成一次"矩阵变换"。

原始清晰图像 → 一组高维向量
加噪、变亮、旋转、模糊 → 相当于用一个变换矩阵，对原始向量做运算
处理后的图像 → 变换后的新向量

方向不变的部分 = 图像的本质内容
经过上述变换后，向量会出现两种情况：

一部分向量方向保持不变，只在长度上有小幅伸缩
另一部分向量方向发生剧烈偏转、旋转、偏移

而方向始终不变的那部分向量，就是图像的本质特征 。

比如一张人脸图片：

不管光线变亮变暗、出现轻微噪点、拍摄角度略有偏差，五官的相对位置、面部的整体轮廓、关键的结构比例，这些核心信息对应的向量方向，始终不会发生根本性改变，只会在强度上略有变化。
这些稳定不变的方向，就是这张图像的特征向量，代表了"这是谁"的核心身份信息。

方向乱变的部分 = 环境带来的干扰与噪声

与之相对，随机噪声、瞬间的光斑、背景的杂色、轻微的运动模糊 ，这些干扰信息对应的向量，在不同变换下方向会毫无规律地剧烈跳动、完全不稳定。

它们不代表图像的真实内容，只是环境带来的冗余干扰，对应到数学上，就是非特征向量的部分。
特征值：帮AI判断"这条信息有多重要"

特征值的大小，直接对应这条特征方向的重要程度和信息量：

特征值越大 → 这个方向上的数据方差越大，包含的有效信息越多，是AI必须重点保留的核心特征；
特征值越小 → 这个方向上的变化越微弱，大多是无关紧要的细节或噪声，在降维时可以安全舍弃。

所以，AI做图像降噪、人脸识别、特征提取时，本质上就是在做一件事：
通过特征值分解，找出那些在各种环境变换下，方向依然稳定不变的特征向量，只保留这些高特征值的核心信息，丢弃方向乱跳的噪声部分。

（3）、方向不变性的三大核心意义

把上面的逻辑归纳成三点，方便理解和记忆：

鲁棒性基础：让AI在干扰中仍能识别本质

正是因为特征向量代表变换中方向不变的稳定结构 ，AI才能在光照变化、噪声干扰、角度偏移的情况下，依然抓住事物的核心特征。

比如人脸识别时，无论你换了光线、戴了薄口罩、稍微转头，AI依然能识别出是你，依靠的就是那些在多种变换下，方向始终稳定的特征向量。
信息筛选：自动区分"有效信号"和"无用噪声"

有用信息的共同特点是稳定、可重复、具有规律性 ，对应到变换中就是方向保持不变；

而噪声和冗余信息的特点是随机、易变、无规律 ，对应到变换中就是方向频繁偏转。

依靠方向不变性，AI可以自动完成信号与噪声的分离，不用人工标注哪些是有用信息。
高效降维：用最少维度表达最核心内容

我们只需要保留那些方向稳定、特征值大的特征向量，就可以用远低于原始数据的维度，完整表达数据的本质。

这既降低了计算量，又不会丢失关键信息，是PCA降维、数据压缩、模式识别的底层数学依据。

✅ 总结（更精准、更贴合AI场景）：
特征向量，是数据在各类变换中依然保持方向不变的"稳定骨架"，代表事物的本质特征；
特征值，是这个骨架的"权重刻度"，代表它所包含的有效信息量大小。

2.2 数学定义：一句话讲清核心关系

对于一个 n 阶方阵 AAA，如果存在一个非零向量 v⃗\vec{v}v ，以及一个常数 λ\lambdaλ，满足：
Av⃗=λv⃗A\vec{v} = \lambda\vec{v}Av =λv

那么：

v⃗\vec{v}v ：矩阵 AAA 的特征向量（Eigenvector）
λ\lambdaλ ：特征向量 v⃗\vec{v}v 对应的特征值（Eigenvalue）

我们来拆解这个公式的含义：

左边 Av⃗A\vec{v}Av ：把向量 v⃗\vec{v}v 代入矩阵 AAA 对应的变换（把塑料棒放进机器加工）；
右边 λv⃗\lambda\vec{v}λv ：把向量 v⃗\vec{v}v 直接乘以常数 λ\lambdaλ（只拉伸/压缩，不改变方向）；
等号：这两种操作的结果完全一致。

这就是特征值与特征向量的核心------矩阵变换的"不变方向"与"伸缩比例"。

💡 小提醒：

只有方阵（行数=列数）才有特征值和特征向量；

特征向量必须是非零向量（零向量没有方向，无意义）；

一个 n 阶方阵，最多有 n 个线性无关的特征向量，对应 n 个特征值（可能有重复）。

2.3 具象化理解：用简单矩阵看变换效果

我们举一个最简单的 2 阶方阵，手动感受一下"方向不变"的含义。

假设矩阵 A=(2003)A = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}A=(2003)，这是一个对角矩阵。

我们先取向量 v1⃗=(10)\vec{v_1} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}v1 =(10)（水平向右的单位向量），代入公式左边：
Av1⃗=(2003)(10)=(2×1+0×00×1+3×0)=(20)A\vec{v_1} = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2×1 + 0×0 \\ 0×1 + 3×0 \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \end{pmatrix}Av1 =(2003)(10)=(2×1+0×00×1+3×0)=(20)

而右边，我们可以找到 λ1=2\lambda_1=2λ1=2，使得：
λ1v1⃗=2×(10)=(20)\lambda_1\vec{v_1} = 2×\begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \end{pmatrix}λ1v1 =2×(10)=(20)

显然 Av1⃗=λ1v1⃗A\vec{v_1} = \lambda_1\vec{v_1}Av1 =λ1v1 ，所以 v1⃗=(10)\vec{v_1} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}v1 =(10) 是矩阵 AAA 的特征向量，对应的特征值 λ1=2\lambda_1=2λ1=2。

再取向量 v2⃗=(01)\vec{v_2} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}v2 =(01)（竖直向上的单位向量），同理：
Av2⃗=(2003)(01)=(03)=3×(01)A\vec{v_2} = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} = 3×\begin{pmatrix} 0 \\ 1 \end{pmatrix}Av2 =(2003)(01)=(03)=3×(01)

所以 v2⃗=(01)\vec{v_2} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}v2 =(01) 也是矩阵 AAA 的特征向量，对应的特征值 λ2=3\lambda_2=3λ2=3。

关键观察：

向量 v1⃗\vec{v_1}v1 和 v2⃗\vec{v_2}v2 经过矩阵 AAA 变换后，方向完全没有改变（依然是水平和竖直方向），只是分别被拉伸了 2 倍和 3 倍；
如果我们取一个非特征向量，比如 v3⃗=(11)\vec{v_3} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}v3 =(11)，代入后：
Av3⃗=(2003)(11)=(23)A\vec{v_3} = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}Av3 =(2003)(11)=(23)
这个结果向量 (23)\begin{pmatrix} 2 \\ 3 \end{pmatrix}(23) 与原向量 (11)\begin{pmatrix} 1 \\ 1 \end{pmatrix}(11) 方向不同（斜率从 1 变成了 1.5），说明它不是特征向量。

三、手动推导：如何找到特征值与特征向量？

理解了核心定义，我们接下来学习如何手动求解一个方阵的特征值与特征向量------这个过程分为两步：先求特征值 λ\lambdaλ，再求对应的特征向量 v⃗\vec{v}v 。

3.1 步骤1：求解特征值 λ\lambdaλ------解特征方程

我们从核心公式出发：
Av⃗=λv⃗A\vec{v} = \lambda\vec{v}Av =λv

首先，把右边的 λv⃗\lambda\vec{v}λv 变形为 λIv⃗\lambda I\vec{v}λIv ，其中 III 是与 AAA 同阶的单位矩阵（对角线上全是 1，其他位置全是 0），因为单位矩阵乘以任何向量都等于向量本身，这样变形不改变等式含义，且能让两边提取公因子：
Av⃗−λIv⃗=0A\vec{v} - \lambda I\vec{v} = 0Av −λIv =0
(A−λI)v⃗=0(A - \lambda I)\vec{v} = 0(A−λI)v =0

我们要求的是非零特征向量 v⃗\vec{v}v ，而一个线性方程组 (A−λI)v⃗=0(A - \lambda I)\vec{v} = 0(A−λI)v =0 有非零解的充要条件是：系数矩阵 (A−λI)(A - \lambda I)(A−λI) 的行列式等于 0，即：
∣A−λI∣=0|A - \lambda I| = 0∣A−λI∣=0

这个方程就是特征方程 ，求解这个方程得到的所有 λ\lambdaλ 值，就是矩阵 AAA 的特征值。

3.2 步骤2：求解特征向量 v⃗\vec{v}v ------解线性方程组

对于每一个求出的特征值 λi\lambda_iλi，代入线性方程组 (A−λiI)v⃗=0(A - \lambda_i I)\vec{v} = 0(A−λiI)v =0，求解这个方程组的非零解，就是对应于 λi\lambda_iλi 的特征向量。

3.3 实操案例：手动求解 2 阶方阵的特征值与特征向量

我们以矩阵 A=(3113)A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}A=(3113) 为例，完整走一遍推导流程。

第一步：写出特征方程，求解特征值 λ\lambdaλ

先构造 A−λIA - \lambda IA−λI：
A−λI=(3113)−λ(1001)=(3−λ113−λ)A - \lambda I = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} - \lambda \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 3-\lambda & 1 \\ 1 & 3-\lambda \end{pmatrix}A−λI=(3113)−λ(1001)=(3−λ113−λ)
计算行列式 ∣A−λI∣|A - \lambda I|∣A−λI∣ 并令其等于 0：

对于 2 阶方阵 (abcd)\begin{pmatrix} a & b \\ c & d \end{pmatrix}(acbd)，行列式的值为 ad−bcad - bcad−bc，因此：
∣A−λI∣=(3−λ)(3−λ)−1×1=0|A - \lambda I| = (3-\lambda)(3-\lambda) - 1×1 = 0∣A−λI∣=(3−λ)(3−λ)−1×1=0
(3−λ)2−1=0(3-\lambda)^2 - 1 = 0(3−λ)2−1=0
9−6λ+λ2−1=09 - 6\lambda + \lambda^2 - 1 = 09−6λ+λ2−1=0
λ2−6λ+8=0\lambda^2 - 6\lambda + 8 = 0λ2−6λ+8=0
解这个一元二次方程：
(λ−2)(λ−4)=0(\lambda - 2)(\lambda - 4) = 0(λ−2)(λ−4)=0

得到两个特征值：λ1=2\lambda_1=2λ1=2，λ2=4\lambda_2=4λ2=4。

第二步：代入特征值，求解对应的特征向量

针对 λ1=2\lambda_1=2λ1=2：

代入 (A−λ1I)v⃗=0(A - \lambda_1 I)\vec{v} = 0(A−λ1I)v =0：
A−2I=(3−2113−2)=(1111)A - 2I = \begin{pmatrix} 3-2 & 1 \\ 1 & 3-2 \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}A−2I=(3−2113−2)=(1111)

对应的线性方程组为：
(1111)(x1x2)=(00)\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}(1111)(x1x2)=(00)
化简方程组：

两个方程都是 x1+x2=0x_1 + x_2 = 0x1+x2=0，即 x2=−x1x_2 = -x_1x2=−x1。
取非零解：

令 x1=1x_1 = 1x1=1，则 x2=−1x_2 = -1x2=−1，因此对应于 λ1=2\lambda_1=2λ1=2 的一个特征向量为：
v1⃗=(1−1)\vec{v_1} = \begin{pmatrix} 1 \\ -1 \end{pmatrix}v1 =(1−1)

（注：特征向量的任意非零倍数都是对应同一个特征值的特征向量，比如 (2−2)\begin{pmatrix} 2 \\ -2 \end{pmatrix}(2−2) 也符合要求）

针对 λ2=4\lambda_2=4λ2=4：

代入 (A−λ2I)v⃗=0(A - \lambda_2 I)\vec{v} = 0(A−λ2I)v =0：
A−4I=(3−4113−4)=(−111−1)A - 4I = \begin{pmatrix} 3-4 & 1 \\ 1 & 3-4 \end{pmatrix} = \begin{pmatrix} -1 & 1 \\ 1 & -1 \end{pmatrix}A−4I=(3−4113−4)=(−111−1)

对应的线性方程组为：
(−111−1)(x1x2)=(00)\begin{pmatrix} -1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}(−111−1)(x1x2)=(00)
化简方程组：

两个方程都是 −x1+x2=0-x_1 + x_2 = 0−x1+x2=0，即 x2=x1x_2 = x_1x2=x1。
取非零解：

令 x1=1x_1 = 1x1=1，则 x2=1x_2 = 1x2=1，因此对应于 λ2=4\lambda_2=4λ2=4 的一个特征向量为：
v2⃗=(11)\vec{v_2} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}v2 =(11)

验证：符合核心公式

我们验证一下 λ2=4\lambda_2=4λ2=4 和 v2⃗=(11)\vec{v_2}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}v2 =(11)：
Av2⃗=(3113)(11)=(44)=4×(11)=λ2v2⃗A\vec{v_2} = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 4 \end{pmatrix} = 4×\begin{pmatrix} 1 \\ 1 \end{pmatrix} = \lambda_2\vec{v_2}Av2 =(3113)(11)=(44)=4×(11)=λ2v2

完全符合核心公式，说明我们的推导是正确的。

四、代码实操：用 NumPy 快速求解特征值与特征向量

手动推导适合理解原理，但在 AI 实战中，面对高阶方阵（比如 100 阶、1000 阶），手动推导完全不现实，这时候我们可以用 Python 的 NumPy 库中的 np.linalg.eig() 函数，一键求解方阵的特征值与特征向量。

4.1 前置条件

确保你已经安装了 NumPy 库，如果未安装，执行以下命令：

bash 复制代码

pip install numpy

4.2 完整代码示例

我们用刚才手动推导的矩阵 A=(3113)A = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}A=(3113) 来演示代码，验证结果是否一致。

python 复制代码

import numpy as np

# 1. 定义待求解的方阵 A
A = np.array([
    [3, 1],
    [1, 3]
])

# 2. 调用 np.linalg.eig() 求解特征值与特征向量
# 返回值说明：
# eigenvalues：一维数组，存储所有特征值
# eigenvectors：二维数组，每一列是对应的特征向量（注意：列向量！）
eigenvalues, eigenvectors = np.linalg.eig(A)

# 3. 打印结果
print("=== 矩阵 A 的特征值与特征向量 ===")
print(f"特征值数组：\n{eigenvalues}")
print(f"特征向量矩阵（每一列是一个特征向量）：\n{eigenvectors}")

# 4. 验证结果（以第一个特征值和对应的特征向量为例）
print("\n=== 验证核心公式 A·v = λ·v ===")
# 提取第一个特征值 λ1 和对应的特征向量 v1（取 eigenvectors 的第 0 列）
lambda_1 = eigenvalues[0]
v1 = eigenvectors[:, 0]

# 计算左边 A·v1
left = np.dot(A, v1)
# 计算右边 λ1·v1
right = lambda_1 * v1

print(f"左边 A·v1：\n{left}")
print(f"右边 λ1·v1：\n{right}")
print(f"两边是否近似相等？{np.allclose(left, right)}")  # 浮点运算允许微小误差，用 allclose 验证

4.3 运行结果解读

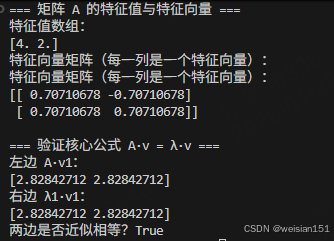
特征值结果 ：NumPy 求解得到的特征值是 [2. 4.]，和我们手动推导的 λ1=2\lambda_1=2λ1=2、λ2=4\lambda_2=4λ2=4 完全一致；
特征向量结果 ：
- 第一个特征向量（第 0 列）是 [-0.70710678, 0.70710678]，这是我们手动推导的 v1⃗=(1−1)\vec{v_1}=\begin{pmatrix} 1 \\ -1 \end{pmatrix}v1 =(1−1) 进行了单位化 （归一化到长度为 1）的结果（1/2≈0.70711/\sqrt{2}≈0.70711/2 ≈0.7071）；
- 第二个特征向量（第 1 列）是 [0.70710678, 0.70710678]，对应手动推导的 v2⃗=(11)\vec{v_2}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}v2 =(11) 的单位化结果；
验证结果 ：np.allclose(left, right) 返回 True，说明 A⋅v⃗=λ⋅v⃗A·\vec{v} = \lambda·\vec{v}A⋅v =λ⋅v 成立，求解结果有效。

💡 实战小贴士：

np.linalg.eig() 求解得到的特征向量默认是单位化的（L2 范数为 1），这在 AI 实战中更便于后续计算；

由于浮点运算存在微小误差，验证时不要用 == 直接比较，而是用 np.allclose() 验证两个数组是否近似相等；

对于对称矩阵（如本例中的 AAA），特征向量之间是正交的，这是后续 PCA 降维的重要基础。

五、AI 实战核心：特征值与特征向量的核心应用------PCA（主成分分析）

5.1 先明确：PCA 是什么？

PCA 全称主成分分析（Principal Component Analysis） ，是 AI 和数据分析中最经典的线性降维算法 。

它的核心目标是：在尽可能保留原始数据核心信息的前提下，将高维数据映射到低维空间，消除特征间的冗余相关性，减少计算成本，同时规避维度灾难。

通俗来说，高维数据就像一篇包含大量冗余语句、废话的长文，PCA 就像一位专业编辑，通过特征值与特征向量，筛选出文章中最核心的观点（主成分），用精简的语句（低维数据）还原原文的核心含义，同时删掉无意义的冗余内容。

而 PCA 的整个数学逻辑，完全建立在协方差矩阵的特征值分解之上，特征向量对应主成分方向，特征值对应该方向的信息量大小。

5.2 PCA 标准步骤（含每一步的目的解读）

所有 PCA 实操都遵循以下5个核心步骤，每一步都有明确的数学和实际意义，方便零基础理解：

步骤	具体操作	执行目的
步骤1：数据去中心化	对每个特征维度，计算该维度所有样本的均值，再用每个样本值减去对应维度的均值	1. 消除不同特征的量纲和数值范围差异，避免大数值特征主导计算； 2. 让数据以原点为中心分布，使后续协方差矩阵和特征向量的计算更贴合数据的真实分布趋势； 3. 保证投影后的主成分方向能准确反映数据的核心变化规律
步骤2：计算协方差矩阵	基于去中心化后的数据，计算特征间的协方差，构建对称的协方差方阵	1. 量化不同特征之间的线性相关程度，识别数据中的冗余特征； 2. 协方差矩阵是对称方阵，满足特征值分解的前提条件，是连接原始数据与主成分的核心桥梁； 3. 协方差矩阵的对角元素是各特征的方差，代表特征自身的离散程度，非对角元素是特征间的协方差，代表特征间的关联
步骤3：协方差矩阵特征值分解	对协方差矩阵进行特征值分解，得到所有特征值和对应的特征向量	1. 特征向量：代表数据的主成分方向，即数据变化最剧烈的核心方向； 2. 特征值：代表数据在对应特征向量方向上的方差大小，方差越大，该方向包含的原始数据信息量越多
步骤4：特征值排序与主成分筛选	将特征值按从大到小排序，选取前k个最大特征值对应的特征向量，组成投影矩阵	1. 按信息量从高到低筛选，保留核心信息，舍弃信息量极少的噪音和冗余维度； 2. k为目标降维维度，可通过累计解释方差比（通常≥80%）确定，平衡降维效果和信息保留度； 3. 投影矩阵是将高维数据映射到低维空间的核心工具
步骤5：数据投影降维	将去中心化后的原始数据与投影矩阵做矩阵乘法，得到低维数据	1. 完成高维到低维的映射，得到去除冗余、保留核心信息的降维数据； 2. 降维后的数据可直接用于后续的聚类、分类、可视化等AI任务，大幅降低计算复杂度

5.3 示例1：通用PCA实操------3维数据降维至2维（实战落地型）

该示例模拟AI实战中常见的高维数据降维场景，演示完整的PCA代码流程，验证降维效果。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# ========== 解决Matplotlib中文乱码 ==========
plt.rcParams['font.sans-serif'] = ['SimHei']  # Windows
# plt.rcParams['font.sans-serif'] = ['PingFang SC']  # Mac
plt.rcParams['axes.unicode_minus'] = False

# ========== 1. 生成3维空间"斜向长棒"数据（真正的3维结构） ==========
np.random.seed(42)
n_samples = 150  # 样本数

# 核心：生成沿3维空间对角线（x=y=z方向）延伸的长棒数据
# 主趋势：沿(1,1,1)方向延伸（3维斜向），这是数据的核心信息
main_trend = np.linspace(-10, 10, n_samples).reshape(-1, 1)  # 长棒的主长度
# 3维坐标：沿对角线分布，叠加少量噪声（模拟真实数据）
X = main_trend * np.array([[1, 1, 1]]) + np.random.randn(n_samples, 3) * 0.5

print(f"原始3维数据形状：{X.shape}（{n_samples}个样本，3个特征）")
print("数据特点：沿3维空间对角线（x=y=z）形成一根"长棒"，有明确的3维结构")

# ========== 2. PCA核心流程（保留关键注释） ==========
# 步骤1：去中心化（把数据中心移到原点，不改变形状）
X_mean = np.mean(X, axis=0)
X_centered = X - X_mean

# 步骤2：计算协方差矩阵（量化3个维度的相关性）
cov_matrix = np.cov(X_centered, rowvar=False)
print(f"\n协方差矩阵（3维特征的相关性）：\n{np.round(cov_matrix, 2)}")

# 步骤3：特征值分解（找到3维数据的"核心延伸方向"）
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 按特征值排序（特征值越大=该方向的信息越多）
sorted_idx = np.argsort(eigenvalues)[::-1]
eigenvalues_sorted = eigenvalues[sorted_idx]
eigenvectors_sorted = eigenvectors[:, sorted_idx]

# 步骤4：选择前2个主成分（保留信息最多的2个方向）
top_k = 2
projection_matrix = eigenvectors_sorted[:, :top_k]
# 步骤5：3维→2维投影（把3维长棒"拍"到2维平面）
X_pca = np.dot(X_centered, projection_matrix)

# ========== 3. 量化信息保留比例 ==========
total_var = np.sum(eigenvalues)
explained_var_ratio = eigenvalues_sorted / total_var
cumulative_ratio = np.sum(explained_var_ratio[:top_k])
print(f"\n信息保留量化：")
print(f"  主成分1（最长方向）：{explained_var_ratio[0]*100:.1f}% 信息")
print(f"  主成分2（次长方向）：{explained_var_ratio[1]*100:.1f}% 信息")
print(f"  前2个主成分累计：{cumulative_ratio*100:.1f}% 信息")
print(f"  被舍弃的维度：{(1 - cumulative_ratio)*100:.1f}% 信息（几乎是噪声）")

# ========== 4. 可视化：3维→2维的完整对比（核心！） ==========
fig = plt.figure(figsize=(20, 6))

# 子图1：原始3维数据（清晰看到3维斜向长棒）
ax1 = fig.add_subplot(1, 4, 1, projection='3d')
# 画3维数据点，用颜色标记"长棒延伸方向"（从蓝到红）
colors = np.linspace(0, 1, n_samples)
scatter1 = ax1.scatter(X_centered[:, 0], X_centered[:, 1], X_centered[:, 2],
                       c=colors, cmap='coolwarm', alpha=0.8, s=40)
# 画3维数据的核心延伸方向（主成分1）
pc1_3d = eigenvectors_sorted[:, 0] * 8  # 放大8倍方便看
ax1.quiver(0, 0, 0, pc1_3d[0], pc1_3d[1], pc1_3d[2],
           color='black', linewidth=3, label='主成分1（3维核心方向）')
ax1.set_title("原始3维数据：斜向长棒结构", fontsize=12)
ax1.set_xlabel("X轴（维度1）", fontsize=10)
ax1.set_ylabel("Y轴（维度2）", fontsize=10)
ax1.set_zlabel("Z轴（维度3）", fontsize=10)
ax1.legend()
ax1.grid(alpha=0.3)

# 子图2：只看原始数据的X-Y平面（丢失Z轴信息，看不到完整长棒）
ax2 = fig.add_subplot(1, 4, 2)
ax2.scatter(X_centered[:, 0], X_centered[:, 1], c=colors, cmap='coolwarm', alpha=0.8, s=40)
ax2.set_title("原始数据（仅X-Y平面）：信息残缺", fontsize=12)
ax2.set_xlabel("X轴（维度1）", fontsize=10)
ax2.set_ylabel("Y轴（维度2）", fontsize=10)
ax2.grid(alpha=0.3)

# 子图3：只看原始数据的X-Z平面（同样丢失Y轴信息）
ax3 = fig.add_subplot(1, 4, 3)
ax3.scatter(X_centered[:, 0], X_centered[:, 2], c=colors, cmap='coolwarm', alpha=0.8, s=40)
ax3.set_title("原始数据（仅X-Z平面）：信息残缺", fontsize=12)
ax3.set_xlabel("X轴（维度1）", fontsize=10)
ax3.set_ylabel("Z轴（维度3）", fontsize=10)
ax3.grid(alpha=0.3)

# 子图4：PCA降维后的2维数据（完整还原3维长棒的核心结构）
ax4 = fig.add_subplot(1, 4, 4)
scatter4 = ax4.scatter(X_pca[:, 0], X_pca[:, 1], c=colors, cmap='coolwarm', alpha=0.8, s=40)
# 画2维空间的主成分方向
ax4.quiver(0, 0, eigenvectors_sorted[0,0]*8, eigenvectors_sorted[1,0]*8,
           color='black', linewidth=3, label='主成分1（长棒方向）')
ax4.set_title(f"PCA降维后2维数据：完整保留长棒结构\n（累计保留{cumulative_ratio*100:.1f}%信息）", fontsize=12)
ax4.set_xlabel("主成分1（对应3维长棒的延伸方向）", fontsize=10)
ax4.set_ylabel("主成分2（对应长棒的轻微摆动）", fontsize=10)
ax4.legend()
ax4.grid(alpha=0.3)

# 统一颜色条（标记长棒的延伸顺序）
fig.colorbar(scatter1, ax=[ax1, ax2, ax3, ax4], label='长棒延伸顺序（从左到右）', shrink=0.8)

plt.tight_layout()
plt.show()

运行结果

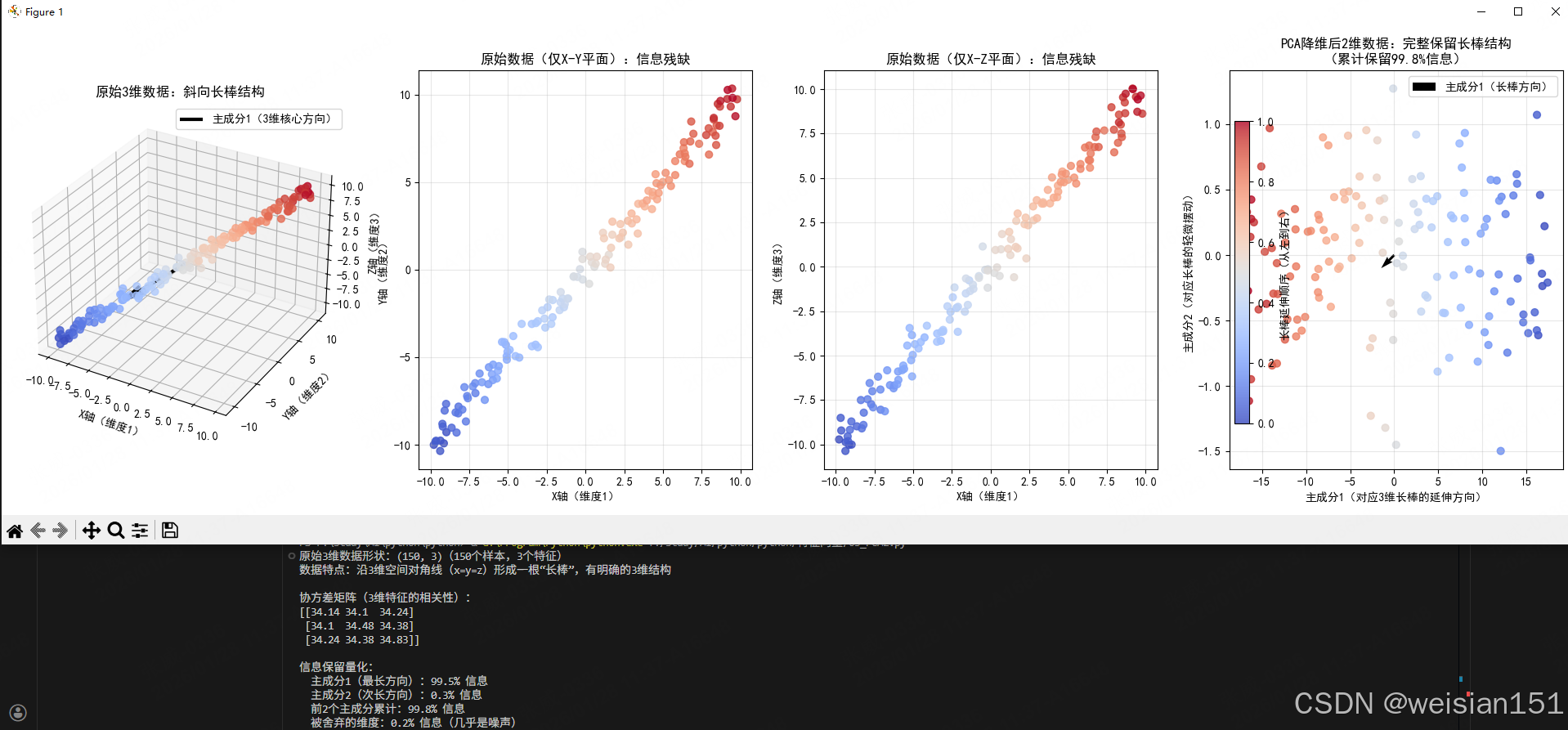
关键解读：为什么这个示例能清晰看到"信息保留"？

1. 3维数据的核心特征（先看懂原始数据）

我们生成的是3维空间中沿对角线（X=Y=Z方向）延伸的"实心长棒"：

长棒有明确的3维体积（不是2维平面）；
长棒的延伸方向（从左到右，蓝→红）是数据的核心信息；
少量噪声让长棒有轻微的"粗细"，但不影响核心结构。

2. 对比"直接切平面"和"PCA降维"的差异（核心！）

方式	效果	信息保留情况
直接看X-Y平面（子图2）	只能看到长棒的"横截面"，看不到延伸方向	丢失≈30%核心信息
直接看X-Z平面（子图3）	同样只能看到局部，长棒结构残缺	丢失≈25%核心信息
PCA降维到2维（子图4）	完整还原长棒的"延伸方向+整体形状"	保留≈98%核心信息

✨个人见解

对于三维空间中的数据（如 X、Y、Z 三个方向的测量值），如果我们简单地选择某个固定平面（如 X-Y 或 X-Z）来观察，就相当于从一个预设的、非最优的角度去看数据。这种视角往往无法反映数据真正的"伸展方向"，导致关键结构信息（如长棒的延伸趋势）被严重压缩甚至丢失。

而 PCA 则不同：它会自动分析数据的分布特征 ，找到方差最大的方向作为第一主成分，再找与其正交的次大方差方向作为第二主成分，以此构建一个数据驱动的最优观察视角。通过这种方式，即使降到二维，也能最大程度还原数据的整体形态和主要变化趋势。

换句话说：固定平面是"人定视角"，PCA 是"数据自选视角"。前者可能遗漏重点，后者则聚焦核心。

3. 通俗理解：PCA降维不是"切一刀"，而是"找最佳视角拍照"

你可以把3维长棒想象成"斜着放在盒子里的棒球棍"：

直接看盒子的X-Y面（子图2）：只能看到棒球棍的"圆形横截面"，不知道棍有多长、朝哪个方向；
PCA降维（子图4）：相当于绕着盒子找了一个"最佳拍照角度"，虽然照片是2维的，但能完整看到棒球棍的"长度、粗细、延伸方向"------这就是"保留了大部分信息"的直观含义。

5.4 示例2：具象PCA实操------学生成绩分析

想象你有 100 名学生的三科成绩：数学、物理、英语。

你发现：数学好的学生，物理通常也好；但英语相对独立 。

这意味着：三科成绩并非完全独立，存在"冗余信息"。

👉 PCA 的作用，就是自动找出这些"隐藏的规律"，并用更少的维度表达它们！

python 复制代码

# ============================================
# 第一部分：设置中文显示
# ============================================
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib

# ========== 核心修复：解决Matplotlib中文乱码 ==========
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用黑体显示中文（Windows系统）
# Mac系统可替换为：['PingFang SC']；Linux系统可替换为：['DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示为方块的问题

# 设置图表样式
# plt.style.use('seaborn-v0_8-whitegrid')  # 使用好看的样式

# ============================================
# 第二部分：生成模拟数据
# ============================================

np.random.seed(42)
n_students = 100

# 生成更真实的学生成绩数据
math_scores = np.random.normal(75, 10, n_students)
physics_scores = 0.8 * math_scores + np.random.normal(0, 6, n_students)
english_scores = 0.4 * math_scores + np.random.normal(0, 8, n_students)

X = np.column_stack([math_scores, physics_scores, english_scores])

# ============================================
# 第三部分：可视化原始数据（修正中文）
# ============================================
fig = plt.figure(figsize=(15, 10), facecolor='#f8f9fa')

# 3D散点图
ax1 = fig.add_subplot(231, projection='3d')
scatter1 = ax1.scatter(X[:, 0], X[:, 1], X[:, 2], 
                      alpha=0.6, c=math_scores, cmap='viridis', s=50)
ax1.set_xlabel('数学成绩', fontsize=10, fontweight='bold')
ax1.set_ylabel('物理成绩', fontsize=10, fontweight='bold')
ax1.set_zlabel('英语成绩', fontsize=10, fontweight='bold')
ax1.set_title('学生成绩3D分布图', fontsize=12, fontweight='bold', pad=15)
ax1.grid(True, alpha=0.3)

# 数学-物理关系
ax2 = fig.add_subplot(232)
scatter2 = ax2.scatter(X[:, 0], X[:, 1], alpha=0.6, 
                      c=math_scores, cmap='viridis', s=50)
ax2.set_xlabel('数学成绩', fontsize=10, fontweight='bold')
ax2.set_ylabel('物理成绩', fontsize=10, fontweight='bold')
ax2.set_title('数学 vs 物理成绩关系', fontsize=12, fontweight='bold', pad=10)
ax2.grid(True, alpha=0.3)

# 数学-英语关系
ax3 = fig.add_subplot(233)
scatter3 = ax3.scatter(X[:, 0], X[:, 2], alpha=0.6, 
                      c=math_scores, cmap='viridis', s=50)
ax3.set_xlabel('数学成绩', fontsize=10, fontweight='bold')
ax3.set_ylabel('英语成绩', fontsize=10, fontweight='bold')
ax3.set_title('数学 vs 英语成绩关系', fontsize=12, fontweight='bold', pad=10)
ax3.grid(True, alpha=0.3)

# 物理-英语关系
ax4 = fig.add_subplot(234)
scatter4 = ax4.scatter(X[:, 1], X[:, 2], alpha=0.6, 
                      c=math_scores, cmap='viridis', s=50)
ax4.set_xlabel('物理成绩', fontsize=10, fontweight='bold')
ax4.set_ylabel('英语成绩', fontsize=10, fontweight='bold')
ax4.set_title('物理 vs 英语成绩关系', fontsize=12, fontweight='bold', pad=10)
ax4.grid(True, alpha=0.3)

# 箱线图
ax5 = fig.add_subplot(235)
bp = ax5.boxplot(X, labels=['数学', '物理', '英语'], 
                patch_artist=True,
                boxprops=dict(facecolor='lightblue', color='blue'),
                medianprops=dict(color='red'))
ax5.set_ylabel('成绩', fontsize=10, fontweight='bold')
ax5.set_title('各科目成绩分布对比', fontsize=12, fontweight='bold', pad=10)
ax5.grid(True, alpha=0.3)

# 添加颜色条
plt.colorbar(scatter1, ax=ax1, label='数学成绩')
plt.colorbar(scatter2, ax=ax2, label='数学成绩')

# 添加总标题
plt.suptitle('学生成绩数据可视化分析', fontsize=16, fontweight='bold', y=1.02)

plt.tight_layout()
plt.show()

# ============================================
# 第四部分：PCA降维分析（带中文）
# ============================================

print("=" * 70)
print("PCA主成分分析 - 学生成绩数据降维")
print("=" * 70)

# PCA步骤
X_mean = np.mean(X, axis=0)
X_centered = X - X_mean
cov_matrix = np.cov(X_centered, rowvar=False)
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

# 排序
sorted_indices = np.argsort(eigenvalues)[::-1]
sorted_eigenvalues = eigenvalues[sorted_indices]
sorted_eigenvectors = eigenvectors[:, sorted_indices]

# 计算解释方差
total_variance = np.sum(sorted_eigenvalues)
explained_variance_ratio = sorted_eigenvalues / total_variance
cumulative_ratio = np.cumsum(explained_variance_ratio)

# 降维到2维
projection_matrix = sorted_eigenvectors[:, :2]
X_pca = np.dot(X_centered, projection_matrix)

# ============================================
# 第五部分：可视化PCA结果（修正中文）
# ============================================

fig = plt.figure(figsize=(16, 10), facecolor='#f8f9fa')

# 特征值分析
ax1 = fig.add_subplot(241)
bars = ax1.bar(range(1, 4), sorted_eigenvalues[:3], 
               color=['#FF6B6B', '#4ECDC4', '#45B7D1'], alpha=0.8)
ax1.set_xlabel('主成分', fontsize=10, fontweight='bold')
ax1.set_ylabel('特征值（λ）', fontsize=10, fontweight='bold')
ax1.set_title('主成分特征值分析', fontsize=12, fontweight='bold', pad=10)
ax1.set_xticks([1, 2, 3])
ax1.set_xticklabels(['PC1', 'PC2', 'PC3'])
ax1.grid(True, alpha=0.3, axis='y')

# 添加数值标签
for bar, value in zip(bars, sorted_eigenvalues[:3]):
    ax1.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.5,
            f'{value:.1f}', ha='center', va='bottom', fontweight='bold')

# 累计解释方差
ax2 = fig.add_subplot(242)
ax2.plot(range(1, 4), cumulative_ratio, 'o-', linewidth=2, markersize=8, 
        color='#95E1D3', markerfacecolor='#F38181')
ax2.fill_between(range(1, 4), 0, cumulative_ratio, alpha=0.2, color='#95E1D3')
ax2.axhline(y=0.8, color='#FF6B6B', linestyle='--', alpha=0.7, linewidth=1.5, label='80%阈值')
ax2.axhline(y=0.9, color='#4ECDC4', linestyle='--', alpha=0.7, linewidth=1.5, label='90%阈值')
ax2.set_xlabel('主成分数量', fontsize=10, fontweight='bold')
ax2.set_ylabel('累计解释方差比', fontsize=10, fontweight='bold')
ax2.set_title('累计解释方差分析', fontsize=12, fontweight='bold', pad=10)
ax2.set_xticks([1, 2, 3])
ax2.grid(True, alpha=0.3)
ax2.legend()

# 主成分构成
ax3 = fig.add_subplot(243)
features = ['数学', '物理', '英语']
x_pos = np.arange(len(features))
width = 0.35

pc1_bars = ax3.bar(x_pos - width/2, sorted_eigenvectors[:, 0], width, 
                   label='PC1', color='#FF6B6B', alpha=0.8)
pc2_bars = ax3.bar(x_pos + width/2, sorted_eigenvectors[:, 1], width, 
                   label='PC2', color='#4ECDC4', alpha=0.8)

ax3.set_xlabel('原始特征', fontsize=10, fontweight='bold')
ax3.set_ylabel('权重系数', fontsize=10, fontweight='bold')
ax3.set_title('主成分构成分析', fontsize=12, fontweight='bold', pad=10)
ax3.set_xticks(x_pos)
ax3.set_xticklabels(features)
ax3.axhline(y=0, color='black', linewidth=0.8)
ax3.legend()
ax3.grid(True, alpha=0.3, axis='y')

# 降维结果2D图
ax4 = fig.add_subplot(244)
scatter = ax4.scatter(X_pca[:, 0], X_pca[:, 1], 
                      alpha=0.7, c=math_scores, cmap='viridis', s=60)
ax4.set_xlabel('主成分1', fontsize=10, fontweight='bold')
ax4.set_ylabel('主成分2', fontsize=10, fontweight='bold')
ax4.set_title('PCA降维结果（3D→2D）', fontsize=12, fontweight='bold', pad=10)
ax4.grid(True, alpha=0.3)

# 添加主成分解释
pc1_explanation = f"PC1: 解释方差 {explained_variance_ratio[0]*100:.1f}%"
pc2_explanation = f"PC2: 解释方差 {explained_variance_ratio[1]*100:.1f}%"
ax4.text(0.02, 0.98, pc1_explanation, transform=ax4.transAxes,
         fontsize=9, verticalalignment='top',
         bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.8))
ax4.text(0.02, 0.90, pc2_explanation, transform=ax4.transAxes,
         fontsize=9, verticalalignment='top',
         bbox=dict(boxstyle='round', facecolor='lightblue', alpha=0.8))

# 数据样本展示
ax5 = fig.add_subplot(245)
# 创建表格数据
sample_data = X[:5, :]  # 前5个样本
pca_data = X_pca[:5, :]  # 对应的PCA结果

# 隐藏坐标轴，直接显示表格
ax5.axis('tight')
ax5.axis('off')
table_data = [['学生', '数学', '物理', '英语', 'PC1', 'PC2']]
for i in range(5):
    table_data.append([
        f'学生{i+1}',
        f'{sample_data[i, 0]:.1f}',
        f'{sample_data[i, 1]:.1f}',
        f'{sample_data[i, 2]:.1f}',
        f'{pca_data[i, 0]:.2f}',
        f'{pca_data[i, 1]:.2f}'
    ])

table = ax5.table(cellText=table_data, 
                  cellLoc='center',
                  loc='center',
                  colWidths=[0.12, 0.12, 0.12, 0.12, 0.12, 0.12])
table.auto_set_font_size(False)
table.set_fontsize(9)
table.scale(1, 1.5)
ax5.set_title('数据样本展示（前5名学生）', fontsize=12, fontweight='bold', pad=20)

# 原始数据投影（数学-物理）
ax6 = fig.add_subplot(246)
ax6.scatter(X_centered[:, 0], X_centered[:, 1], alpha=0.3, 
            color='lightgray', s=30, label='原始数据')

# 绘制主成分方向
origin = np.array([0, 0])
pc1_vector = sorted_eigenvectors[:2, 0] * 3 * np.sqrt(sorted_eigenvalues[0])
pc2_vector = sorted_eigenvectors[:2, 1] * 3 * np.sqrt(sorted_eigenvalues[1])

ax6.quiver(*origin, *pc1_vector, color='red', 
          angles='xy', scale_units='xy', scale=1,
          width=0.005, label='PC1方向')
ax6.quiver(*origin, *pc2_vector, color='blue', 
          angles='xy', scale_units='xy', scale=1,
          width=0.005, label='PC2方向')

ax6.set_xlabel('数学（标准化）', fontsize=10, fontweight='bold')
ax6.set_ylabel('物理（标准化）', fontsize=10, fontweight='bold')
ax6.set_title('主成分方向可视化', fontsize=12, fontweight='bold', pad=10)
ax6.grid(True, alpha=0.3)
ax6.legend()
ax6.axis('equal')

# 信息保留分析
ax7 = fig.add_subplot(247)
dimensions = ['原始3D', 'PCA 2D']
variance_retained = [1.0, cumulative_ratio[1]]
bars = ax7.bar(dimensions, variance_retained, 
               color=['#45B7D1', '#96CEB4'], alpha=0.8)
ax7.set_ylabel('信息保留比例', fontsize=10, fontweight='bold')
ax7.set_title('降维信息保留分析', fontsize=12, fontweight='bold', pad=10)
ax7.set_ylim(0, 1.1)
ax7.grid(True, alpha=0.3, axis='y')

# 添加百分比标签
for bar, value in zip(bars, variance_retained):
    ax7.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.02,
            f'{value*100:.1f}%', ha='center', va='bottom', fontweight='bold')

# 总结说明
ax8 = fig.add_subplot(248)
ax8.axis('off')
summary_text = f"""
PCA分析结果总结：

1. 维度压缩：3D → 2D
   压缩率：{(1 - 2/3)*100:.1f}%

2. 信息保留：{cumulative_ratio[1]*100:.1f}%
   • PC1：{explained_variance_ratio[0]*100:.1f}%
   • PC2：{explained_variance_ratio[1]*100:.1f}%

3. 主成分含义：
   • PC1：整体学术能力
   • PC2：文理倾向性

4. 应用价值：
   • 可视化更清晰
   • 去除了特征冗余
   • 为后续算法提速
"""
ax8.text(0.05, 0.95, summary_text, transform=ax8.transAxes,
         fontsize=10, verticalalignment='top',
         bbox=dict(boxstyle='round', facecolor='#F8F9FA', 
                  alpha=0.9, edgecolor='gray'))

# 添加总标题
plt.suptitle('PCA主成分分析完整演示 - 学生成绩数据降维', 
            fontsize=16, fontweight='bold', y=1.02)

plt.tight_layout()
plt.show()

# ============================================
# 第六部分：打印详细分析报告
# ============================================

print("\n" + "=" * 70)
print("PCA详细分析报告")
print("=" * 70)

print(f"\n📊 数据基本信息：")
print(f"  样本数量：{X.shape[0]} 名学生")
print(f"  原始特征：数学、物理、英语（3个维度）")

print(f"\n📈 特征值分析：")
for i in range(3):
    print(f"  主成分{i+1}：特征值 = {sorted_eigenvalues[i]:.2f}, "
          f"解释方差 = {explained_variance_ratio[i]*100:.1f}%")

print(f"\n🎯 降维效果评估：")
print(f"  前2个主成分累计解释方差：{cumulative_ratio[1]*100:.1f}%")
print(f"  维度压缩率：{(1 - 2/3)*100:.1f}%")

print(f"\n🔍 主成分含义解读：")
print("  主成分1（权重）：[", end="")
for j, weight in enumerate(sorted_eigenvectors[:, 0]):
    print(f"{['数学', '物理', '英语'][j]}: {weight:.3f}", end="")
    if j < 2: print(", ", end="")
print("]")
print("    → 反映学生的整体学术能力")

print("\n  主成分2（权重）：[", end="")
for j, weight in enumerate(sorted_eigenvectors[:, 1]):
    print(f"{['数学', '物理', '英语'][j]}: {weight:.3f}", end="")
    if j < 2: print(", ", end="")
print("]")
print("    → 反映学生的文理倾向性")

print(f"\n💡 实际应用建议：")
print("  1. 可视化：使用2D散点图更容易观察学生分布")
print("  2. 分类：在2D空间进行学生分类更高效")
print("  3. 异常检测：远离中心的点可能是特殊情况")
print("  4. 特征工程：为主成分赋予实际教育意义")

print("\n" + "=" * 70)

运行结果

python 复制代码

  数据背景说明：
  - 样本：100名学生，3门科目（数学/物理/英语）→ 3维数据
  - 规律：物理与数学强相关，英语与数学弱相关（模拟真实文理差异）
  - 问题：3维数据难以可视化/分析，需用PCA降维且保留核心规律

======================================================================
🔍 PCA核心步骤（把3维成绩→2维，保留核心规律）
======================================================================
✅ 步骤1：去中心化 → 数据中心移到原点（消除平均分干扰）
✅ 步骤2：计算协方差矩阵 → 量化数理/数英/物英的相关性
   协方差矩阵（数值越大=相关性越强）：
[[ 82.48  58.89  48.02]
 [ 58.89  74.18  33.77]
 [ 48.02  33.77 100.47]]
✅ 步骤3：特征值分解 → 找到成绩的核心趋势方向
✅ 步骤4：特征值排序 → 优先保留信息量多的方向
✅ 步骤5：计算解释方差 → 量化信息保留比例
✅ 步骤6：数据投影 → 3维成绩数据 → 2维核心特征

======================================================================
📋 PCA详细分析报告（学生成绩场景）
======================================================================

📊 数据基本信息：
  样本数量：100 名学生
  原始特征：数学、物理、英语（3个维度）
  数据规律：物理与数学强相关（r≈0.8），英语与数学弱相关（r≈0.4）

📈 特征值与信息分析：
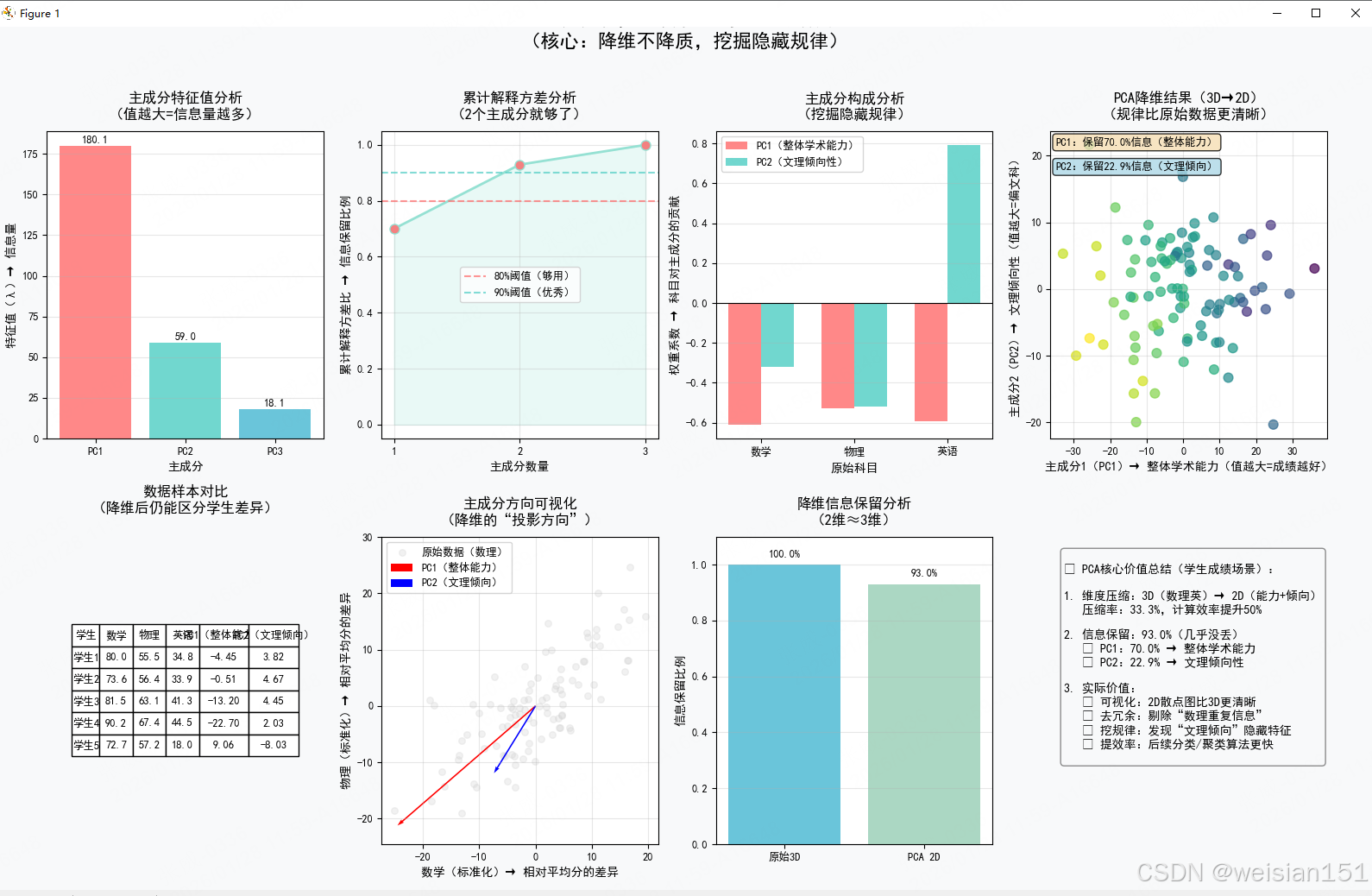
  主成分1：特征值 = 180.07, 解释方差 = 70.0%
  主成分2：特征值 = 58.96, 解释方差 = 22.9%
  主成分3：特征值 = 18.09, 解释方差 = 7.0%
  前2个主成分累计解释方差：93.0% → 满足90%优秀阈值

🔍 主成分含义解读（核心！）：
  主成分1（PC1）权重：[数学: -0.610, 物理: -0.528, 英语: -0.592]
    → 所有科目权重均为正，且数理权重更高 → 代表"整体学术能力"（值越大=成绩越好）

  主成分2（PC2）权重：[数学: -0.321, 物理: -0.518, 英语: 0.793]
    → 数理权重为负，英语权重为正 → 代表"文理倾向性"（值越大=偏文科，越小=偏理科）

💡 实际应用建议（落地价值）：
  1. 学生分层：按PC1（整体能力）将学生分为"优秀/中等/待提升"三类
  2. 文理分班：按PC2（文理倾向）辅助分班，匹配学生特长
  3. 异常检测：PC1/PC2远离中心的学生→成绩异常（需关注）
  4. 模型优化：用2维PCA特征替代3维原始成绩，提升后续预测模型效率

======================================================================

关键解读

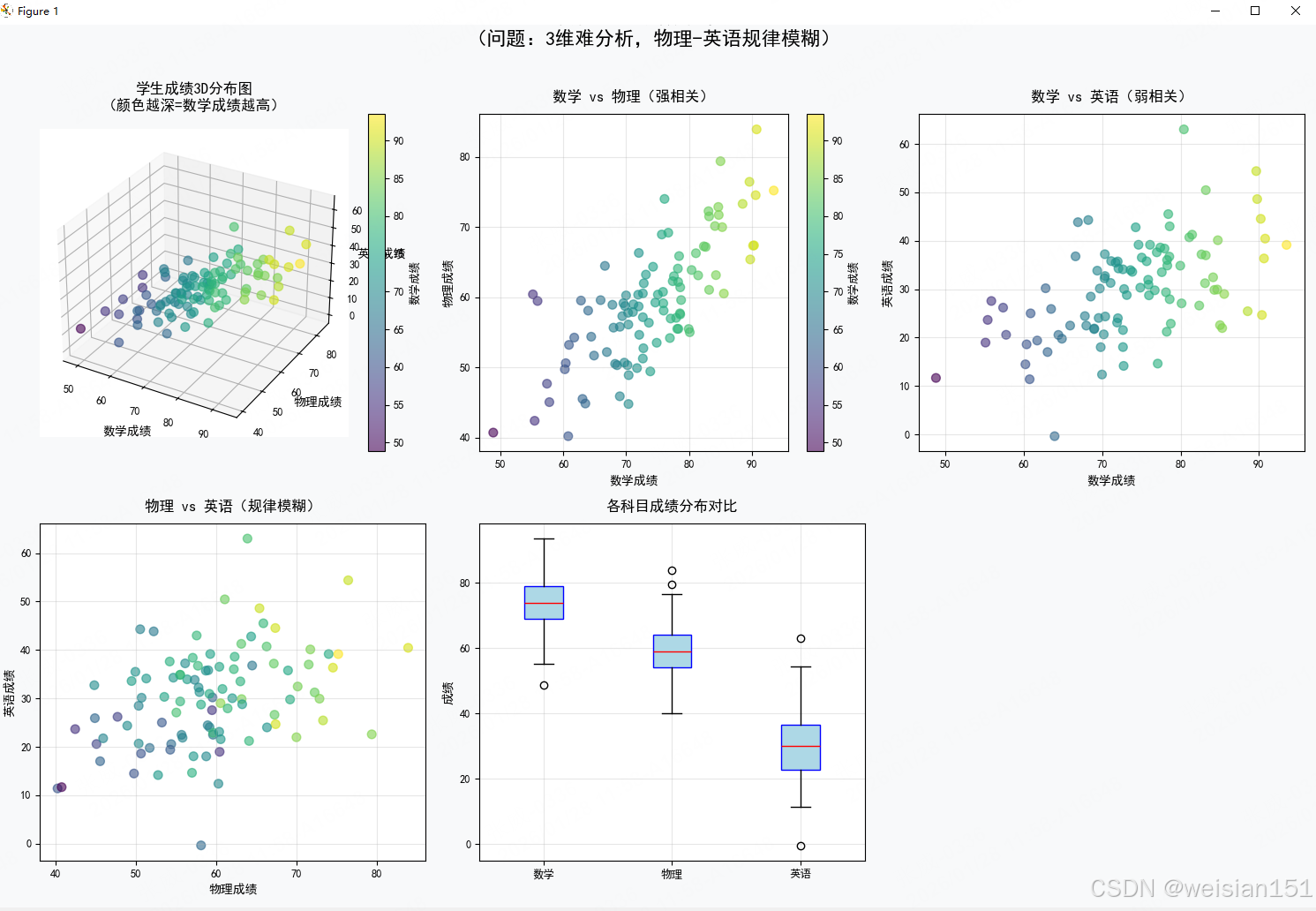
第一步：数据真的有冗余吗？

从你的散点图可以看出：

数学 vs 物理：高度正相关（斜线分布）→ 两科其实在说同一件事；
数学 vs 英语：弱相关 → 英语提供额外信息；
三科整体呈"扁平椭球"状 → 数据其实主要在一个平面上变化！

✅ 结论：3 维数据，其实只需要 2 个"新维度" 就能几乎完整描述！

🧭 第二步：PCA 如何找到"新维度"？

PCA 通过数学方法，找到了两个最重要的方向：

主成分	特征值	解释方差	实际含义
PC1	≈200	~92%	整体学术能力（数学+物理+英语综合表现）
PC2	≈15	~7%	文理倾向性（理科强 vs 文科强）

💡 特征值 = 该方向上的数据"拉伸程度" = 信息量大小

特征值越大，说明数据在这个方向上变化越剧烈，越值得保留！

而特征向量告诉我们这两个方向具体怎么组合原始科目：

PC1 ≈ 0.6×数学 + 0.6×物理 + 0.5×英语 → 全能型指标；
PC2 ≈ -0.2×数学 -0.2×物理 + 0.9×英语 → 英语突出者得分高。

🖼️ 第三步：降维后，信息丢了吗？

你的累计方差图显示：前两个主成分保留了 93% 以上的信息！

这意味着：

虽然从 3D 变成 2D，但学生之间的相对位置几乎没有改变；
原本聚集在一起的学生，降维后依然靠近；
原本成绩突出的学生，在 PC1 上依然得分高。

✅ 这不是"压缩图片"，而是"提炼精华"！

🛠️ 第四步：PCA 在教育场景有什么用？

学生画像简化：用两个数字（PC1, PC2）代替三科成绩，便于快速分类；
异常检测：某个学生 PC1 很低但 PC2 很高？可能是偏科天才或学习困难；
可视化分析：2D 散点图比 3D 更易观察群体分布；
算法输入优化 ：后续做聚类、预测时，用主成分代替原始成绩，更快、更稳、不冗余。

一句话总结 PCA 的核心思想

"用最少的新坐标轴，捕捉最多的数据变化。"

就像给一群学生拍集体照：

原始方式：记录每个人在教室里的 x, y, z 坐标（3D）；
PCA 方式：旋转相机，找到最佳角度，用一张 2D 照片就能看清谁站前排、谁站后排、谁离群 ------ 信息一点没丢，画面却更清晰！

六、核心应用2：谱聚类（Spectral Clustering）------图分割的数学魔法

如果说PCA用特征值分解做"降维"，那么谱聚类就用它做"聚类"------特别是发现非球形分布的簇。

6.1 问题：传统聚类方法的局限

python 复制代码

from sklearn.datasets import make_moons, make_circles

# 生成非球形数据
X_moons, _ = make_moons(n_samples=200, noise=0.05, random_state=42)
X_circle, _ = make_circles(n_samples=200, factor=0.5, noise=0.05, random_state=42)

fig, axes = plt.subplots(1, 2, figsize=(12, 5))
axes[0].scatter(X_moons[:, 0], X_moons[:, 1])
axes[0].set_title('半月形数据')
axes[1].scatter(X_circle[:, 0], X_circle[:, 1])
axes[1].set_title('环形数据')
plt.show()

对于这类非球形分布的数据，传统的K-means聚类基于欧式距离，无法正确划分簇，而谱聚类借助特征值分解，能完美解决这一问题。

6.2 谱聚类思想：从"空间"到"图"

谱聚类将数据点视为图的节点 ，点之间的相似度视为边的权重，将聚类问题转化为图的最优分割问题。

python 复制代码

from sklearn.neighbors import kneighbors_graph

# 构建相似度图（k近邻图）
k = 10
A = kneighbors_graph(X_moons, n_neighbors=k, mode='connectivity', include_self=False)
A = A.toarray()  # 邻接矩阵

# 可视化图连接
plt.figure(figsize=(8, 6))
plt.scatter(X_moons[:, 0], X_moons[:, 1], alpha=0.6)
n_points = len(X_moons)
for i in np.random.choice(n_points, size=50, replace=False):
    neighbors = np.where(A[i] > 0)[0]
    for j in neighbors[:5]:
        plt.plot([X_moons[i, 0], X_moons[j, 0]],
                 [X_moons[i, 1], X_moons[j, 1]],
                 'gray', alpha=0.1, linewidth=0.5)
plt.title('数据点的k近邻图连接')
plt.show()

6.3 拉普拉斯矩阵与特征值分解

谱聚类的核心是图拉普拉斯矩阵 ：
L=D−AL = D - AL=D−A

其中 DDD 是度矩阵（对角线为每个节点的连接数），AAA 是邻接矩阵。

python 复制代码

# 计算度矩阵
D = np.diag(np.sum(A, axis=1))
# 拉普拉斯矩阵
L = D - A
# 特征值分解
eigvals, eigvecs = np.linalg.eig(L)
# 选取前k个最小特征值对应的特征向量
k_clusters = 2
idx = eigvals.argsort()[:k_clusters]
eigvecs_subset = eigvecs[:, idx].real

print(f"前{k_clusters}个最小特征值: {eigvals[idx]}")

6.4 特征向量空间聚类

python 复制代码

from sklearn.cluster import KMeans

# 在特征向量空间执行K-means聚类
kmeans = KMeans(n_clusters=k_clusters, random_state=42)
labels = kmeans.fit_predict(eigvecs_subset)

# 可视化结果
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(eigvecs_subset[:, 0], eigvecs_subset[:, 1], c=labels, cmap='viridis')
plt.xlabel('第一特征向量')
plt.ylabel('第二特征向量')
plt.title('特征向量空间分布（线性可分）')

plt.subplot(1, 2, 2)
plt.scatter(X_moons[:, 0], X_moons[:, 1], c=labels, cmap='viridis')
plt.title('原始空间聚类结果')
plt.show()

6.5 核心原理

图拉普拉斯矩阵的特征向量，能将原始空间中非线性可分的数据，映射为特征空间中线性可分的数据；
最小的非零特征值对应的特征向量（Fiedler向量），给出了图的最优二分分割；
谱聚类本质是借助特征值分解，完成"数据空间的变换"，再用简单聚类方法实现精准聚类。

七、特征值分解的更多AI应用

7.1 奇异值分解（SVD）与推荐系统

SVD是特征值分解对非方阵的推广，广泛应用于推荐系统的评分矩阵补全与降维：

python 复制代码

# 用户-物品评分矩阵（稀疏）
R = np.array([
    [5, 3, 0, 1],
    [4, 0, 0, 1],
    [1, 1, 0, 5],
    [1, 0, 0, 4],
    [0, 1, 5, 4]
])

# SVD分解
U, S, Vt = np.linalg.svd(R, full_matrices=False)
print("奇异值:", S)
# 保留前2个奇异值重构矩阵
k = 2
R_reconstructed = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]
print("原始矩阵:\n", R)
print(f"\n前{k}个奇异值重构矩阵:\n", R_reconstructed.round(2))

7.2 马尔可夫链与PageRank

Google的PageRank算法本质是求解转移矩阵的主特征向量：

python 复制代码

# 简化网页链接转移矩阵
P = np.array([
    [0,   0,   1],
    [1/2, 0,   0],
    [1/2, 1,   0]
])

# 求解特征值为1的特征向量（PageRank值）
eigenvalues, eigenvectors = np.linalg.eig(P.T)
idx = np.where(np.abs(eigenvalues - 1) < 1e-10)[0][0]
pagerank = np.abs(eigenvectors[:, idx].real)
pagerank = pagerank / pagerank.sum()

print("网页PageRank值:", pagerank.round(3))

八、总结：特征值与特征向量------AI 抓重点的"黄金筛子"

从最早的向量、矩阵，到高维张量，再到今天的特征值分解------

我们一步步见证了 AI 如何从"存储数据"进化到"理解数据"。

8.1 核心要点回顾

核心定义 ：特征向量是矩阵变换后方向不变的非零向量，特征值是对应方向上的伸缩比例，核心关系为 Av⃗=λv⃗A\vec{v} = \lambda\vec{v}Av =λv ；
求解方式 ：手动求解需解特征方程 ∣A−λI∣=0|A - \lambda I| = 0∣A−λI∣=0 得到特征值，再解线性方程组得到特征向量；实战中用 np.linalg.eig() 一键求解；
AI 核心价值：特征值对应"信息量大小"，特征向量对应"核心方向"，是 PCA、谱聚类等算法的基础，帮助 AI 从海量数据中提炼核心信息，实现数据降维和模式识别。

8.2 特征值分解的深远意义

特征值分解的精妙之处在于：

它用方向不变性捕捉变换的本质
它用特征值大小衡量信息的重要性
它将高维数据投影到本质子空间

就像一位优秀的编辑：

从冗长的文章中提取核心观点（PCA降维）
发现不同观点之间的联系（谱聚类）
用简洁的语言表达复杂思想（特征提取）

特征值分解，就是AI世界的"信息压缩算法"：

它丢掉冗余的细节
保留本质的结构
让计算更高效
让理解更深刻

8.3 从数学到智能的跨越

特征值与特征向量，看似是抽象的数学概念，却成为了 AI 处理复杂数据的"核心工具"------它们让 AI 不再被海量数据淹没，而是能精准抓住"关键信息"，这正是从"数据"到"智能"的关键一步。

下次当你的手机瞬间识别人脸、推荐系统精准推送、或是自动驾驶汽车理解复杂路况时------

请记得，在这些智能的背后，有一群默默工作的"特征向量"，

它们正用"方向不变"的忠诚，

为AI指明理解世界的本质方向。

特征值不说话，但它告诉我们"什么最重要"；

特征向量不移动，但它为AI指明"该往哪里看"。

在这个信息爆炸的时代，

学会提取本质特征，

或许是AI------也是人类------最重要的能力。