数据结构-栈

免费版Java学习笔记（28w字）链接：https://www.yuque.com/aoyouaoyou/sgcqr8

免费版Java面试题（20w字）链接：https://www.yuque.com/aoyouaoyou/wh3hto

完整版可在小红书搜索：遨游qk0

一、栈的概念

1. 基础定义

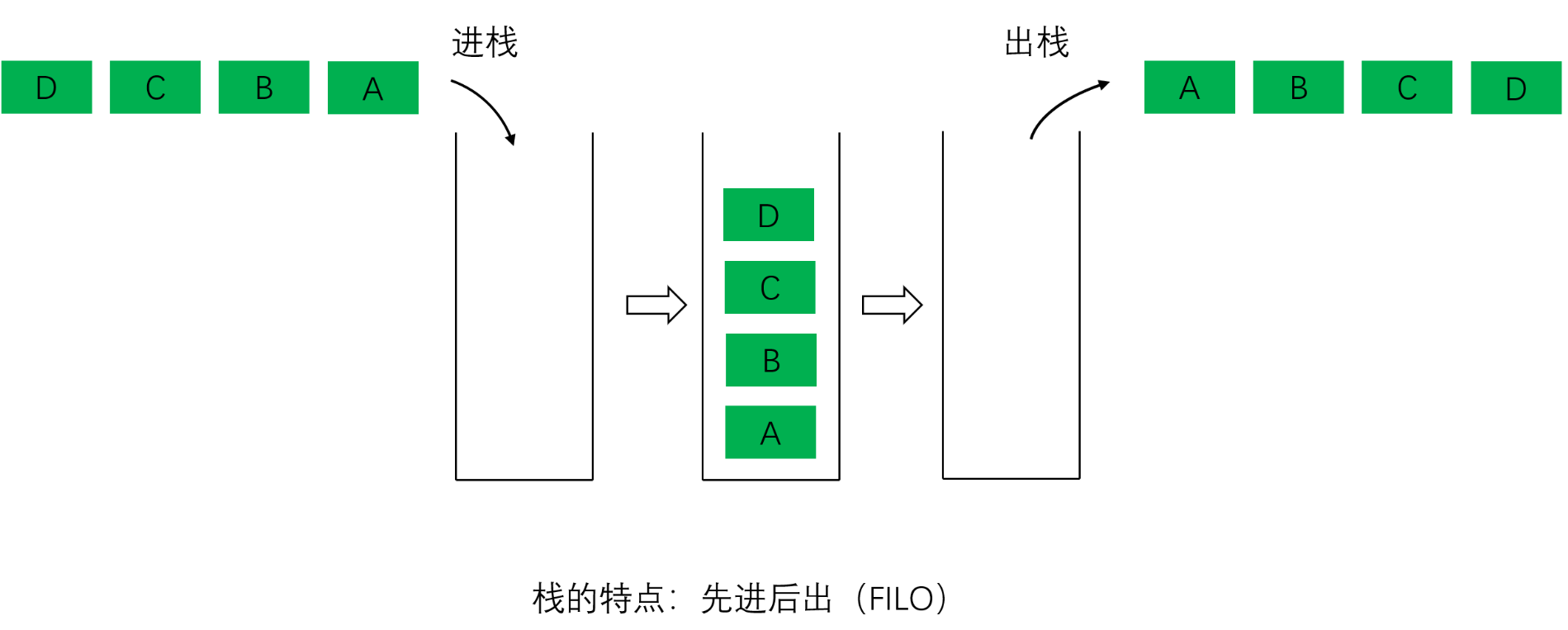
栈是遵循先入后出（FILO，First In Last Out） 规则的线性逻辑结构，元素仅能从一端操作，是受限的线性表。

2. 术语

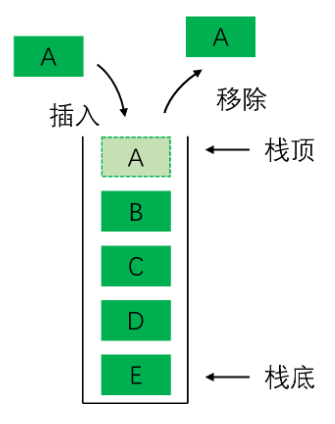
• 栈底：最早进入栈的元素存放位置，栈的固定一端，元素入栈后栈底位置不变；
• 栈顶：最后进入栈的元素存放位置，栈的活动一端，入栈/出栈均围绕栈顶操作；
• 入栈（push）：将新元素添加到栈顶的操作；
• 出栈（pop）：将栈顶元素从栈中移除并返回的操作。

3. 存储特性

栈是逻辑结构，可通过两种物理结构实现，无固定存储方式：

• 数组实现：顺序栈（静态栈/动态扩容栈）；
• 链表实现：链式栈（动态栈）。

二、栈的两种实现方式

方式1：数组实现顺序栈（含判空/判满，基础版无扩容）

数组实现的栈依托连续内存，用数组 存储元素、变量记录栈顶位置，操作简单、访问高效，也叫静态栈。

/**
 * 数组实现顺序栈（基础版，固定容量，支持push/pop/peek/判空/判满）
 * 栈顶指针：size-1（size为栈中元素个数，初始0）
 */
public class ArrayStack {
    // 存储栈元素的数组
    private final Integer[] stackArr;
    // 栈中实际元素个数（兼栈顶指针：size-1为栈顶元素下标）
    private int size;

    // 构造方法：初始化栈的容量
    public ArrayStack(int capacity) {
        if (capacity <= 0) {
            throw new IllegalArgumentException("栈容量必须大于0！");
        }
        stackArr = new Integer[capacity];
        size = 0;
    }

    // 入栈操作：元素压入栈顶，返回是否成功
    public boolean push(Integer data) {
        if (isFull()) {
            System.out.println("栈已满，入栈失败！");
            return false;
        }
        stackArr[size] = data; // 新元素放入栈顶位置
        size++; // 栈顶指针后移
        return true;
    }

    // 出栈操作：栈顶元素弹出，返回弹出元素（栈空返回null）
    public Integer pop() {
        if (isEmpty()) {
            System.out.println("栈为空，出栈失败！");
            return null;
        }
        size--; // 栈顶指针前移
        Integer topData = stackArr[size];
        stackArr[size] = null; // 清空原栈顶位置，避免内存残留
        return topData;
    }

    // 查看栈顶元素：仅返回不弹出（栈空返回null）
    public Integer peek() {
        if (isEmpty()) {
            return null;
        }
        return stackArr[size - 1];
    }

    // 判空：栈中是否无元素
    public boolean isEmpty() {
        return size == 0;
    }

    // 判满：栈是否达到最大容量
    public boolean isFull() {
        return size == stackArr.length;
    }

    // 测试主方法
    public static void main(String[] args) {
        ArrayStack stack = new ArrayStack(5);
        // 入栈
        stack.push(10);
        stack.push(20);
        stack.push(30);
        System.out.println("当前栈顶元素：" + stack.peek()); // 输出30
        // 出栈
        System.out.println(stack.pop()); // 输出30
        System.out.println(stack.pop()); // 输出20
        // 空栈/满栈测试
        stack.push(40);
        stack.push(50);
        stack.push(60);
        stack.push(70); // 栈容量5，此时已满
        stack.push(80); // 提示栈已满，入栈失败
        System.out.println(stack.pop()); // 输出70
    }
}

方式2：链表实现链式栈（头节点作为栈顶，无需考虑容量）

链表实现的栈依托链式存储，用头节点作为栈顶，入栈/出栈仅修改头节点指针，无需提前指定容量，也叫动态栈。

/**
 * 链表节点定义（链式栈专用，数据域为整型）
 */
public class StackNode {
    // 数据域：存储节点值
    public int data;
    // 指针域：指向下一个节点
    public StackNode next;

    public StackNode(int data) {
        this.data = data;
    }
}

/**
 * 链表实现链式栈（头节点为栈顶，支持push/pop/peek/判空，无容量限制）
 */
public class LinkedStack {
    // 头节点（栈顶）：入栈/出栈均操作头节点
    private StackNode top;
    // 栈中元素个数
    private int size;

    // 构造方法：初始化空栈
    public LinkedStack() {
        top = null;
        size = 0;
    }

    // 入栈操作：新节点作为新栈顶（头插法）
    public void push(int data) {
        StackNode newNode = new StackNode(data);
        newNode.next = top; // 新节点指向原栈顶
        top = newNode;      // 新节点成为新栈顶
        size++;
    }

    // 出栈操作：栈顶节点弹出，返回节点值（栈空抛出异常）
    public int pop() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空，无法执行出栈操作！");
        }
        StackNode oldTop = top; // 记录原栈顶
        top = top.next;         // 原栈顶的下一个节点成为新栈顶
        oldTop.next = null;     // 断开原栈顶的指针，避免内存泄漏
        size--;
        return oldTop.data;
    }

    // 查看栈顶元素：仅返回不弹出（栈空抛出异常）
    public int peek() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空，无栈顶元素！");
        }
        return top.data;
    }

    // 判空：栈中是否无元素
    public boolean isEmpty() {
        return top == null || size == 0;
    }

    // 获取栈中元素个数
    public int getSize() {
        return size;
    }

    // 测试主方法
    public static void main(String[] args) {
        LinkedStack stack = new LinkedStack();
        // 入栈
        stack.push(100);
        stack.push(200);
        stack.push(300);
        System.out.println("当前栈顶元素：" + stack.peek()); // 输出300
        System.out.println("栈中元素个数：" + stack.getSize()); // 输出3
        // 出栈
        System.out.println(stack.pop()); // 输出300
        System.out.println(stack.pop()); // 输出200
        System.out.println("出栈后栈顶元素：" + stack.peek()); // 输出100
    }
}

两种实现细节

1. 顺序栈 ：栈顶由size控制，size-1为栈顶元素下标，入栈/出栈本质是数组的下标操作，需注意栈满限制；
2. 链式栈 ：采用头插法 实现，头节点始终是栈顶，入栈/出栈仅修改头节点指针，无容量限制，无需判满；
3. 均增加peek()方法（查看栈顶不弹出），是实际开发中常用的栈操作，弥补原示例的功能缺失。

三、栈的时间复杂度

基础版栈（固定容量顺序栈/链式栈）

入栈（push）、出栈（pop）、查看栈顶（peek）的时间复杂度均为 O(1)，仅涉及固定次数的指针/下标操作，无元素遍历或移动。

支持动态扩容的顺序栈

1. 扩容逻辑 ：当顺序栈满时，创建原容量2倍的新数组，将原数组元素拷贝到新数组，再执行入栈；
2. 时间复杂度：

• • 无扩容时，入栈仍为O(1)；
  • 触发扩容时，需拷贝数组元素，入栈时间复杂度为 O(n)（n为栈中元素个数）；
  • 均摊后整体入栈时间复杂度仍为O(1)，扩容为低频操作。

1. 链式栈无需扩容，始终保持O(1)的入栈/出栈效率。

四、栈的优缺点

顺序栈（数组实现）

优点

• 随机访问特性，栈顶操作效率高，CPU缓存命中率高；
• 实现简单，无额外内存开销（仅存储数据，无需指针）。

缺点

• 基础版有容量限制，满栈后无法入栈；
• 动态扩容版触发扩容时，有数组拷贝的时间开销，且扩容后可能存在内存浪费。

链式栈（链表实现）

优点

• 无容量限制，只要内存有空闲，可无限入栈；
• 无需扩容，入栈/出栈始终稳定在O(1)。

缺点

• 每个节点需存储指针域，有额外的内存开销；
• 节点分散存储，CPU缓存命中率低，遍历/操作效率略低于顺序栈。

五、栈的经典实际应用

栈的先入后出 特性适配所有"后进先处理"的业务场景，是开发中高频使用的线性结构，经典应用如下：

1. 程序的函数调用栈

• 原理：JVM/编译器会为每个函数调用创建栈帧 （存储临时变量、返回地址、参数等），函数调用时栈帧入栈 ，函数执行完成返回时，栈帧出栈；
• 特性：最后调用的函数最先执行完成（后进先出），保证函数调用的嵌套顺序正确；
• 示例：A调用B，B调用C → 栈帧入栈顺序A→B→C，出栈顺序C→B→A。

此处为语雀内容卡片，点击链接查看：https://www.yuque.com/aoyouaoyou/pbz18g/aqywumy8eluhhwn8

2. 浏览器的前进/后退功能

• 原理：使用两个栈（X：后退栈，Y：前进栈） 实现，利用栈的FILO特性记录页面访问顺序；
• 操作：

1. 1. 首次浏览页面：依次压入栈X，栈Y清空；
   2. 点击后退：栈X的栈顶元素出栈，压入栈Y，展示出栈的页面；
   3. 点击前进：栈Y的栈顶元素出栈，压入栈X，展示出栈的页面；
   4. 边界判断：栈X空则无法后退，栈Y空则无法前进。

3. 其他高频应用

• 表达式求值：如计算器解析算术表达式（中缀转后缀/前缀），利用栈处理运算符的优先级；
• 括号匹配：如校验代码中的()/[]/{}是否成对，左括号入栈，右括号与栈顶匹配出栈；
• 深度优先搜索（DFS）：如树/图的遍历，利用栈记录遍历路径，实现回溯。

六、总结

1. 栈是FILO的受限线性逻辑结构，入栈/出栈仅能操作栈顶，操作是push、pop、peek；
2. 物理实现分顺序栈（数组） 和链式栈（链表），基础版均为O(1)时间复杂度，链式栈无容量限制，顺序栈需考虑扩容；
3. 顺序栈适合容量固定、读操作频繁 的场景，链式栈适合频繁增删、容量不固定的场景；
4. 栈的价值在于维护操作的顺序性，适配"后进先处理"的场景，是函数调用、表达式解析、回溯算法的基础。